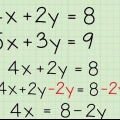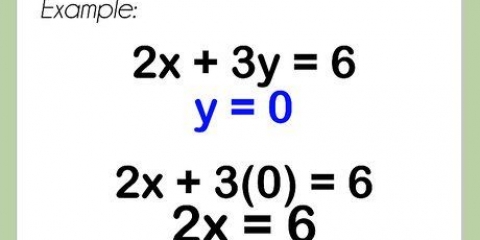Calculer l'intersection de deux lignes (avec des images)

Teneur

Pas
- Méthode 1 sur 2: Détermination de l`intersection entre deux lignes droites
- Méthode 2 sur 2: Problèmes avec les équations quadratiques
Des astuces

Lorsque des lignes droites se coupent sur un graphique à deux dimensions, elles le font en un seul point, indiqué par les coordonnées x et y. Puisque les deux lignes passent par ce point, vous savez que les coordonnées x et y doivent satisfaire les deux équations. Avec quelques techniques supplémentaires, vous pouvez trouver les intersections de paraboles et d`autres courbes quadratiques, en utilisant la même logique.

Pas

Méthode 1 sur 2: Détermination de l`intersection entre deux lignes droites

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 1

1. Écrire l`équation de n`importe quelle droite avec y à gauche. Si nécessaire, modifiez l`équation pour que y soit isolé d`un côté du signe égal. Si l`équation est écrite avec f(x) ou g(x) au lieu de y, séparez ce terme. N`oubliez pas que vous pouvez éliminer des termes en effectuant la même opération des deux côtés.

Les équations sont-elles inconnues, puis le déterminer sur la base des informations fournies.
Exemple: Supposons que vous ayez deux lignes $oui = X + 3$ $y=x+3$ et $oui - 12 = - 2 X$ $y-12=-2x$ . Pour séparer y dans la deuxième équation, ajoutez 12 de chaque côté : $oui = 12 - 2 X$ $y=12-2x$

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 2

2. Assurez-vous que les côtés droits des équations sont égaux. Nous recherchons un point où les deux lignes ont les mêmes valeurs x et y ; c`est le point d`intersection des lignes. Les deux équations n`ont qu`un y à gauche, nous savons donc que les côtés droits sont égaux l`un à l`autre. Écrivez une nouvelle équation montrant ceci.

Exemple: nous savons que

oui = X + 3

$y=x+3$ et

oui = 12 - 2 X

$y=12-2x$ , Et ainsi $X + 3 = 12 - 2 X$ $x+3=12-2x$ .

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 3

3. Résoudre x dans l`équation. La nouvelle équation n`a qu`une seule variable, x. Résoudre cela avec l`algèbre, en effectuant la même opération des deux côtés. Trouvez les termes x de chaque côté de l`équation et placez-les sous la forme x = __ (si ce n`est pas possible, continuez à lire à la fin de cette section).

Exemple:

X + 3 = 12 - 2 X

$x+3=12-2x$

téléphoner

2 X

$2x$ de chaque côté:

3 X + 3 = 12

$3x+3=12$

Soustraire 3 de chaque côté :

3 X = 9

$3x=9$

Divisez chaque côté par 3:

X = 3

$x=3$ .

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 4

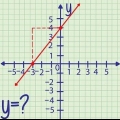
4. Utilisez cette valeur x pour résoudre y. Choisissez l`équation de chaque droite. Remplacez chaque x dans l`équation par la réponse que vous avez trouvée. Résolvez maintenant pour y.

Exemple:

X = 3

$x=3$ et

oui = X + 3

$y=x+3$

oui = 3 + 3

$y=3+3$

oui = 6

$y=6$

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 5

5. Vérifie ton travail. Il est sage de brancher votre valeur x dans l`autre équation pour voir si vous obtenez le même résultat. Si vous obtenez une autre solution pour y, revenez en arrière et vérifiez votre travail pour les erreurs.

Exemple:

X = 3

$x=3$ et

oui = 12 - 2 X

$y=12-2x$

oui = 12 - 2 (3)

$y=12-2(3)$

oui = 12 - 6

$y=12-6$

$oui = 6$ $y=6$

C`est la même réponse que précédemment. Nous n`avons fait aucune erreur.

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 6

6. Notez les coordonnées x et y de l`intersection. Vous avez maintenant résolu pour la valeur x et la valeur y de l`intersection des deux lignes. Écrivez le point sous forme de coordonnée, avec la valeur x comme premier nombre.

Exemple:

X = 3

$x=3$ et

oui = 6

$y=6$

Les deux droites se coupent au point (3.6).

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 7

sept. Traiter les résultats inhabituels. Certaines équations rendent impossible la résolution de x. Cela ne signifie pas nécessairement que vous avez fait une erreur. Une paire de lignes peut conduire à une solution spéciale de deux manières :

Si les deux droites sont parallèles elles ne se couperont pas . Les termes x peuvent être éliminés et votre équation peut être simplifiée en une équation invalide (telle que

0 = 1

$0=1$ ). Notez ici`les lignes ne se coupent pas ou pas une solution valable` si tu réponds.

Si les deux équations décrivent la même droite, alors elles « se coupent » partout. Vous pouvez éliminer les termes x et simplifier votre équation en une équation valide (telle que

3 = 3

$3=3$ ). écrire `les deux lignes sont les mêmes` comme réponse.

Méthode 2 sur 2: Problèmes avec les équations quadratiques

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 8

1. Apprendre à reconnaître les équations du second degré. Dans une équation quadratique, il y a une ou plusieurs variables sous forme quadratique (

X 2

$x^{2}$ ou

oui 2

$y^{2}$ ), et il n`y a pas de puissances supérieures. Les droites représentées par des équations sont courbes, et peuvent donc couper une droite en 0, 1 ou 2 points. Dans cette partie, vous apprendrez à trouver les intersections d`un tel problème.

Calculez les équations entre parenthèses pour voir si elles sont quadratiques. Par exemple, $oui = (X + 3) (X)$ $y=(x+3)(x)$ est quadratique, car vous pouvez le mettre en dehors des parenthèses si $oui = X 2 + 3 X .$ $y=x^{2}+3x$
Avoir des équations d`un cercle ou d`une ellipse les deux une $X 2$ $x^{2}$ comme un $oui 2$ $y^{2}$ terme. Si vous trouvez ces cas particuliers difficiles, lisez la suite Conseils à la fin de cet article.

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 9

2. Écrire les équations en fonction de y. Si nécessaire, réécrivez chaque équation de sorte que y soit d`un côté.

Exemple: Trouver l`intersection de

X 2 + 2 X - oui = - 1

$x^{2}+2x-y=-1$ et

oui = X + sept

$y=x+7$ .

Réécrivez l`équation quadratique en fonction de y :

$oui = X 2 + 2 X + 1$ $y=x^{2}+2x+1$ et $oui = X + sept$ $y=x+7$ .

Cet exemple a une équation quadratique et une équation linéaire. Les problèmes avec deux équations quadratiques sont résolus de la même manière.

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 10

3. Combinez les deux équations pour éliminer le y. Si vous avez rendu les deux équations égales à y, alors vous savez que les deux équations sans y sont égales l`une à l`autre.

Exemple:

oui = X 2 + 2 X + 1

$y=x^{2}+2x+1$ et

oui = X + sept

$y=x+7$

$X 2 + 2 X + 1 = X + sept$ $x^{2}+2x+1=x+7$

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 11

4. Réorganiser la nouvelle équation de sorte qu`un côté soit égal à zéro. Utilisez des méthodes mathématiques standard pour obtenir tous les termes d`un côté de l`équation. Il s`agit de la configuration requise des problèmes pour pouvoir les résoudre à l`étape suivante.

Exemple:

X 2 + 2 X + 1 = X + sept

$x^{2}+2x+1=x+7$

Soustraire x de chaque côté :

X 2 + X + 1 = sept

$x^{2}+x+1=7$

Soustraire 7 de chaque côté :

$X 2 + X - 6 = 0$ $x^{2}+x-6=0$

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 12

5.Résoudre l`équation quadratique. Si vous avez un côté égal à zéro, il y a trois façons de résoudre l`équation quadratique. Tout le monde préfère une méthode différente. Vous pouvez en savoir plus sur la formule quadratique de `diviser le carré`, ou vous pouvez suivre cet exemple plus loin pour cela factoriser méthode:

Exemple:

X 2 + X - 6 = 0

$x^{2}+x-6=0$

Le but de la factorisation est de déterminer les deux facteurs multipliés ensemble pour produire cette équation. Dès le premier terme, on sait que

X 2

$x^{2}$ peut être divisé en x, et x. Écrivez (x )(x ) = 0 pour montrer ceci.

Le dernier terme est -6. Écrivez chaque paire de facteurs qui se sont multipliés pour donner -6 comme produit :

- 6 * 1

$-6*1$ ,

- 3 * 2

$-3*2$ ,

- 2 * 3

$-2*3$ , et

- 1 * 6

$-1*6$ .

Le terme moyen est x (que vous pouvez écrire comme 1x). Additionnez chaque paire de facteurs pour obtenir 1 comme réponse. La bonne paire de facteurs est

- 2 * 3

$-2*3$ , parce que

- 2 + 3 = 1

$-2+3=1$ .

Complétez les lacunes de votre réponse avec ces quelques facteurs : $(X - 2) (X + 3) = 0$ $(x-2)(x+3)=0$ .

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 13

6. Gardez les yeux ouverts pour deux solutions pour x. Si vous travaillez trop vite, vous pouvez trouver une réponse au problème sans vous rendre compte qu`il y en a une autre. Voici comment trouver les deux valeurs x pour les lignes qui se coupent en deux points :

Exemple (facteur) : On aboutit à l`équation

(X - 2) (X + 3) = 0

$(x-2)(x+3)=0$ . Si les deux facteurs entre parenthèses sont égaux à 0, alors l`équation est vraie. La seule solution est

X - 2 = 0

$x-2=0$ → $X = 2$ $x=2$ . L`autre solution est

X + 3 = 0

$x+3=0$ → $X = - 3$ $x=-3$ .

Exemple (équation quadratique ou carré divisant) : Si vous utilisez l`une de ces méthodes pour résoudre l`équation, une racine carrée apparaîtra. Par exemple, notre équation devient

X = (- 1 + \sqrt{25}) / 2

$x=(-1+{sqrt{25}})/2$ . N`oubliez pas que vous pouvez simplifier une racine carrée en deux solutions différentes :

\sqrt{25} = 5 * 5

${sqrt{25}}=5*5$ , et

\sqrt{25} = (- 5) * (- 5)

${sqrt{25}}=(-5)*(-5)$ . Écrivez deux équations, une pour chaque possibilité, et résolvez x pour chacune d`elles.

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 14

sept. Résoudre des problèmes avec une ou zéro solution. Deux lignes qui se touchent à peine ont une intersection, et deux lignes qui ne se touchent jamais ont zéro. Vous pouvez les reconnaître des manières suivantes :

Une solution : Les problèmes peuvent être divisés en deux facteurs identiques ((x-1)(x-1) = 0). Entré dans la formule quadratique, la racine carrée . devient

\sqrt{0}

${sqrt{0}}$ . Vous n`avez qu`à résoudre une équation.

Il n`y a pas de vraie solution : Il n`y a pas de facteurs qui répondent aux exigences (liste à moyen terme). Entré dans la formule quadratique, vous obtenez un nombre négatif sous le radical (tel que

\sqrt{- 2}

${sqrt{-2}}$ ). Écrivez « pas de solution » comme réponse.

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 15

8. Rebranchez les valeurs x dans l`équation d`origine. Une fois que vous avez la valeur x de l`intersection, remettez-la dans l`une des équations avec lesquelles vous avez commencé. Résoudre y pour trouver la valeur y. S`il y a une deuxième valeur x, répétez pour cette valeur également.

Exemple: Nous avons trouvé deux solutions,

X = 2

$x=2$ et

X = - 3

$x=-3$ . Une de nos droites a l`équation

oui = X + sept

$y=x+7$ . remplacer

oui = 2 + sept

$y=2+7$ et

oui = - 3 + sept

$y=-3+7$ , et résolvez chaque équation pour obtenir

oui = 9

$y=9$ et

oui = 4

$y=4$ si tu as une réponse.

Image intitulée Trouver algébriquement l`intersection de deux lignes Étape 16

9. Écrivez la réponse sous forme de coordonnées. Maintenant, vous écrivez la réponse sous forme de coordonnées, avec la valeur x et la valeur y de l`intersection. Si vous avez deux réponses, assurez-vous de faire correspondre la valeur x correcte avec chaque valeur y.

Exemple: quand nous

X = 2

$x=2$ entrée, on obtient

oui = 9

$y=9$ , de sorte qu`un point d`intersection est égal à (2, 9). Nous faisons la même chose pour la deuxième solution , et cela nous donne le point d`intersection (-3, 4) au.

Des astuces

Les équations pour un cercle ou une ellipse ont un $X 2$ $x^{2}$ terme et une $oui 2$ $y^{2}$ terme. Pour trouver l`intersection d`un cercle et d`une ligne droite, résolvez x à l`intérieur de l`équation linéaire. Remplacez la solution de x dans l`équation du cercle, et l`équation quadratique est devenue beaucoup plus facile. Ces problèmes peuvent avoir 0, 1 ou 2 solutions, comme déjà indiqué dans les méthodes ci-dessus.
Un cercle et une parabole (ou toute autre équation quadratique) peuvent avoir 0, 1, 2, 3 ou 4 solutions. Trouvez la variable qui est un carré dans les deux équations - disons que c`est x. lâche $X 2$ $x^{2}$ et remplacez la réponse par $X 2$ $x^{2}$ dans l`autre équation. Résoudre y pour trouver les solutions 0, 1 ou 2. Rebranchez chaque solution dans l`équation quadratique d`origine et résolvez x. Chacun d`eux peut avoir 0, 1 ou 2 solutions.