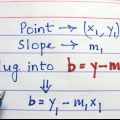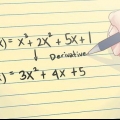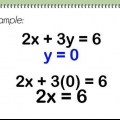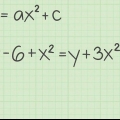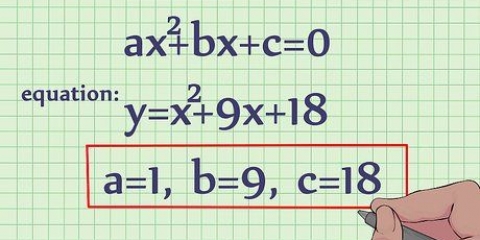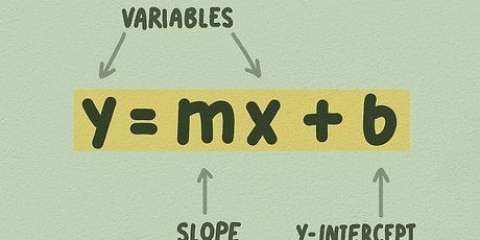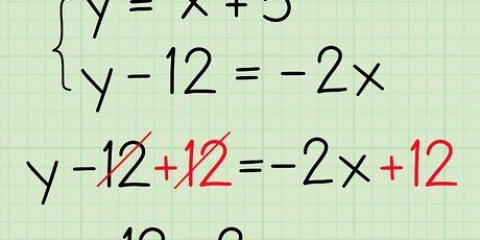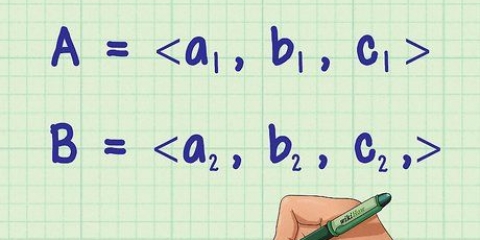Trouver l'intersection d'une équation avec l'axe Y

Teneur

Pas
Des astuces

L`ordonnée à l`origine d`une équation est le point où le graphique d`une équation coupe l`axe des y. Il y a plusieurs façons de trouver cette intersection, selon les informations données au début de votre commande.

Pas

Méthode 1 sur 3 : Recherche de l`intersection avec l`axe des y, en utilisant la pente

Image intitulée Find the Y Intercept Step 1

1. Notez la pente. La pente de « y sur x » est un nombre unique qui indique la pente d`une ligne. Ce type de problème vous donne également la (x, y)-coordonnée d`un point sur le graphique. Si vous n`avez pas ces deux détails, continuez avec les autres méthodes ci-dessous.

Exemple 1: Une ligne droite avec pente 2 passe par le point (-3.4). Déterminez l`intersection avec l`axe des y de cette ligne en suivant les étapes ci-dessous.

Image intitulée Find the Y Intercept Step 2

2. Apprendre la forme habituelle d`une équation linéaire. Toute ligne droite peut s`écrire sous la forme y = mx + b. Lorsque l`équation est sous cette forme, est m la pente et la constante b l`intersection avec l`axe des y.

Image intitulée Find the Y Intercept Step 3

3. Substituer la pente dans cette équation. Écrivez l`équation linéaire, mais au lieu de m utilises-tu la pente de ta droite.

Exemple 1 (suite) :y = mx + b
m = pente = 2
y = 2x + b

Image intitulée Find the Y Intercept Step 4

4. Remplacer x et y par les coordonnées du point. Si vous avez les coordonnées d`un point sur la ligne, vous pouvez X et oui-remplacer les coordonnées du X et oui dans ton équation linéaire. Faites ceci pour la comparaison de votre affectation.

Exemple 1 (suite) : Le point (3,4) est sur cette droite. À ce point, x = 3 et y = 4.
Remplacez ces valeurs par oui = 2X +b:
4 = 2(3) + b

Image intitulée Find the Y Intercept Step 5

5. Résoudre pour b. Ne pas oublier, b est l`intersection avec l`axe des y de la droite. À présent b est la seule variable de l`équation, réorganisez l`équation à résoudre pour cette variable et trouvez la réponse.

Exemple 1 (suite) :4 = 2(3) + b
4 = 6 + b
4 - 6 = b
-2 = b
L`intersection de cette ligne avec l`axe des y est -2.

Image intitulée Find the Y Intercept Step 6

6. Écrivez-le comme une coordonnée. L`intersection avec l`axe des y est le point d`intersection de la ligne avec l`axe des y. Puisque l`axe des y passe par le point x = 0, la coordonnée x de l`intersection avec l`axe des y est toujours 0.

Exemple 1 (suite) : L`intersection avec l`axe des y est à y = -2, donc le point de coordonnée est (0, -2).

Méthode 2 sur 3: Utiliser deux points

Image intitulée Find the Y Intercept Step 7

1. Notez les coordonnées des deux points. Cette méthode traite des problèmes dans lesquels seuls deux points sont donnés sur une ligne droite. Écrivez chaque coordonnée sous la forme (x,y).

Image intitulée Find the Y Intercept Step 8

2. Exemple 2 : Une droite passe par les points (1, 2) et (3, -4). Déterminez l`intersection avec l`axe des y de cette ligne en suivant les étapes ci-dessous.

Image intitulée Find the Y Intercept Step 9

3. Calculer les valeurs x et y. La pente ou la pente est une mesure de combien la ligne se déplace dans le sens vertical pour chaque pas dans le sens horizontal. Vous le savez peut-être sous le nom de « y sur x » (

\frac{oui}{X}

${frac{y}{x}}$ ). Voici comment déterminer ces valeurs à l`aide de deux points :

Le changement de `y` est le changement de direction verticale, ou la différence entre le oui-valeurs des deux points.

Le changement de « x » est le changement de direction horizontale, ou la différence entre le X-valeurs des deux points.

Exemple 2 (suite) : Les valeurs y des deux points sont 2 et -4, donc la ligne augmente dans la direction verticale avec (-4) - (2) = -6.
Les valeurs x des deux points (dans le même ordre) sont 1 et 3, donc la ligne augmente horizontalement de 3 - 1 = 2.

Image intitulée Find the Y Intercept Step 10

4. Divisez y par x pour déterminer la pente. Maintenant que vous connaissez ces deux valeurs, vous pouvez les utiliser dans `

\frac{oui}{X}

${frac{y}{x}}$ ` pour déterminer la pente de la droite.

Exemple 2 (suite) :

s je ô p e = \frac{oui}{X} = - 6 2 =

$pente={frac{y}{x}}={frac{-6}{2}}=$ -3.

Image intitulée Find the Y Intercept Step 11

5. Jetez un autre regard sur la forme standard d`une équation linéaire. Vous pouvez décrire une ligne droite avec la formule y = mx + b, par lequel m la pente est et b l`intersection avec l`axe des y. Maintenant que nous avons la pente m et un point (x,y), nous pouvons utiliser cette équation pour trouver b à résoudre (l`intersection avec l`axe des y).

Image intitulée Find the Y Intercept Step 12

6. Remplissez la pente et le point dans l`équation. Prenez l`équation sous forme standard et remplacez m par la pente que vous avez calculée. Remplacer les variables X et oui par les coordonnées d`un seul point sur la ligne. Peu importe le point que vous utilisez.

Exemple 2 (suite): y = mx + b
Pente = m = -3, donc y = -3x + b
La droite passe par un point de coordonnées (x,y) (1,2), donc 2 = -3(1) + b.

Image intitulée Find the Y Intercept Step 13

sept. Résoudre pour b. Maintenant, la seule variable qui reste dans l`équation est b, l`intersection avec l`axe des y. Réorganiser l`équation de sorte que b d`un côté de l`équation, et vous avez votre réponse. Rappelez-vous que l`intersection avec l`axe des y a toujours une coordonnée x de 0.

Exemple 2 (suite): 2 = -3(1) + b
2 = -3 + b
5 = b
L`intersection avec l`axe des y est (0,5).

Méthode 3 sur 3: Utilisation d`une équation

Image intitulée Find the Y Intercept Step 14

1. Écris l`équation de la droite. Si vous avez l`équation de la droite, vous pouvez déterminer l`intersection avec l`axe des y avec un peu d`algèbre.

Exemple 3: Quelle est l`intersection avec l`axe des y de la ligne x + 4y = 16?
Remarque : l`exemple 3 est une ligne droite. Voir la fin de cette section pour un exemple d`équation quadratique (utilisant une variable élevée à la puissance 2).

Image intitulée Find the Y Intercept Step 15

2. Remplacez x par 0. L`axe des y est une ligne verticale passant par x = 0. Cela signifie que tout point sur l`axe des y a une coordonnée x de 0, y compris l`intersection de la ligne avec l`axe des y. Entrez 0 pour x dans l`équation.

Exemple 3 (suite): x + 4y = 16
x = 0
0 + 4 ans = 16
4 ans = 16

Image intitulée Find the Y Intercept Step 16

3. Résoudre pour y. La réponse est l`intersection de la ligne avec l`axe des y.

Exemple 3 (suite): 4a = 16

4 oui 4 = \frac{16}{4}

${frac{4y}{4}}={frac{16}{4}}$
y = 4.
L`intersection de la ligne avec l`axe des y est 4.

Image intitulée Find the Y Intercept Step 17

4. Confirmez-le en dessinant un graphique (facultatif). Vérifiez votre réponse en traçant l`équation aussi précisément que possible. Le point où la ligne passe par l`axe des y est l`intersection avec l`axe des y.

Image intitulée Find the Y Intercept Step 18

5. Trouver l`intersection avec l`axe des y d`une équation quadratique. Une équation quadratique a une variable (x ou y) élevée à la puissance 2. En utilisant la même substitution, vous pouvez résoudre pour y, mais comme l`équation quadratique est une courbe, elle peut couper l`axe des y à 0, 1 ou 2 points. Cela signifie que vous vous retrouverez avec 0, 1 ou 2 réponses.

Exemple 4: Pour trouver l`intersection de

oui 2 = X + 1

$y^{2}=x+1$ avec l`axe des y, vous substituez x = 0 et résoudre l`équation quadratique.
Dans ce cas on peut

oui 2 = 0 + 1

$y^{2}=0+1$ résoudre en prenant la racine carrée des deux côtés. N`oubliez pas que vous obtenez deux réponses lorsque vous prenez une racine carrée : une réponse négative et une réponse positive.

\sqrt{oui} 2 = \sqrt{1}

${sqrt{y^{2}}}={sqrt{1}}$
y = 1 ou y = -1. Ce sont tous deux l`intersection avec l`axe des y de cette courbe.

Des astuces

Certains pays utilisent un c ou toute autre variable pour b dans l`équation y = mx + b. Son sens, cependant, reste le même; c`est juste une notation différente.
Pour des équations plus compliquées, vous pouvez utiliser les termes avec oui isoler d`un côté de l`équation.
Lors du calcul de la pente entre deux points, vous pouvez X et oui-soustraire les coordonnées dans n`importe quel ordre, tant que vous mettez le point dans le même ordre pour y et x. Par exemple, la pente entre (1, 12) et (3, 7) peut être calculée de deux manières différentes :

Deuxième point – premier point : $sept - 12 3 - 1 = - 5 2 = - 2.5$ ${frac{7-12}{3-1}}={frac{-5}{2}}=-2.5$
Premier point – deuxième point : $12 - sept 1 - 3 = 5 - 2 = - 2.5$ ${frac{12-7}{1-3}}={frac{5}{-2}}=-2.5$