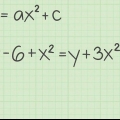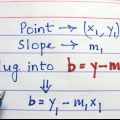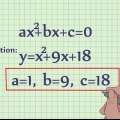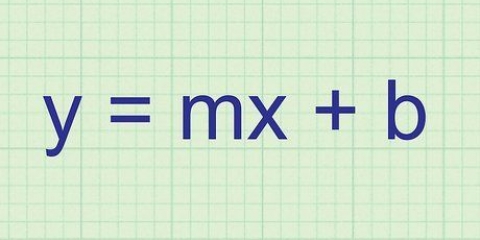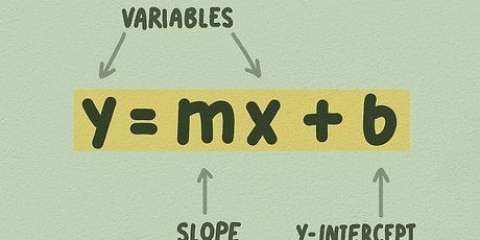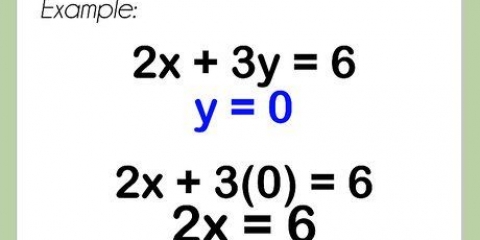Trouver l'équation d'une ligne tangente : 4 étapes (avec des photos)

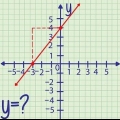
Une tangente à une parabole ou à une courbe est une ligne qui ne touche la courbe qu`à un point donné. Pour trouver l`équation de cette tangente, vous devrez calculer la pente de la courbe en ce point, ce qui nécessite quelques calculs mathématiques. Vous pouvez alors écrire l`équation de la ligne tangente sous une forme point-pente. Cet article explique les étapes à suivre.

Pas

Image intitulée Trouver l`équation d`une ligne tangente Étape 1

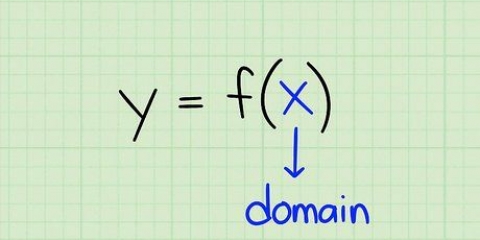
1. L`équation d`une courbe peut être exprimée en fonction. Trouver la dérivée de cette fonction pour trouver l`équation de la pente de cette courbe.

Le moyen le plus simple de différencier la plupart des polynômes consiste à utiliser la règle de la chaîne. Multipliez chaque équation de la fonction par sa puissance pour trouver le coefficient de ce terme dans la dérivée, puis soustrayez la puissance par 1.
Exemple : Pour la fonction f(x) = x^3 + 2x^2 + 5x + 1, la dérivée est f`(x) = 3x^2 + 4x + 5.
Pour f(x) = (2x+5)^10 + 2*(4x+3)^5, la dérivée est f`(x) = 10*2*(2x+5)^9 + 2*5*4 *(4x+3)^4 = 20*(2x+5)^9 + 40*(4x+3)^4.

Image intitulée Trouver l`équation d`une ligne tangente Étape 2

2. Si tout va bien, les coordonnées où la ligne tangente rencontre la courbe sont données. Branchez la valeur x de ce point, dans la fonction dérivée, pour trouver la pente de la courbe en ce point.

Pour x = 2, le point sur la courbe est (2.27) car f(2) = 2^3 + 2*2^2 + 5*2 + 1 = 27.

Pour f`(x) = 3x^2 + 4x + 5, la pente est en (2.27) est f`(2) = 3(2)^2 + 4(2) + 5 = 25.

Image intitulée Trouver l`équation d`une ligne tangente Étape 3

3. Cette pente est aussi la pente de la tangente. Vous avez maintenant la pente et le point de cette ligne, vous pouvez donc écrire l`équation de la ligne sous forme point-pente, ou y - y1 = m(x - x1).

Sous la forme point-pente, est m la pente et (x1,y1) sont les coordonnées du point. Donc dans cet exemple, l`équation devient y - 27 = 25 (x - 2).

Image intitulée Trouver l`équation d`une ligne tangente Étape 4

4. Il peut également être nécessaire de convertir cette équation sous une autre forme pour obtenir la réponse finale, si les instructions qui accompagnent le problème l`exigent.