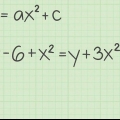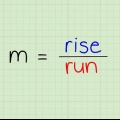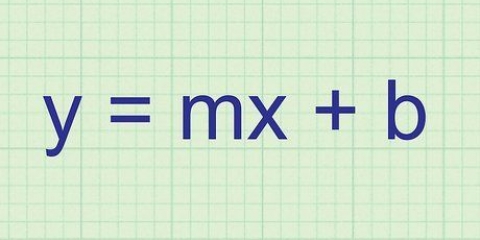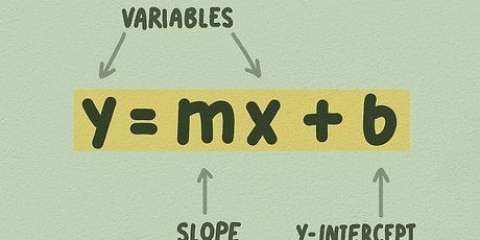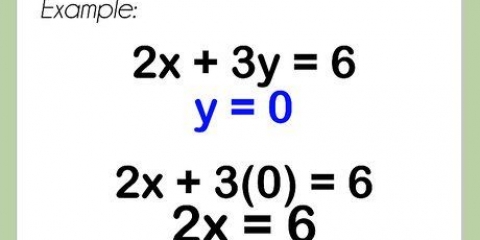Un point et une pente sont donnés. Deux points sont donnés, mais pas de pente. Étant donné un point et une autre ligne parallèle à celui-ci. Étant donné un point et une autre ligne perpendiculaire à celui-ci. 




Réorganisez votre équation. b = y - mx. Entrez les valeurs et résolvez. b = -5 - (2/3)6. b = -5 - 4. b = -9 Vérifiez que l`intersection avec l`axe des y est bien -9. Écrivez l`équation : y = 2/3 x - 9 

Utilisez votre pente et vos coordonnées dans l`équation ci-dessus. Multipliez la pente (m) avec l`abscisse du point. Soustraire la valeur de la coordonnée y du point. tu as maintenant b résolu, l`intersection avec l`axe des y. 



Calculer la pente. La pente = (Y2 - Oui1) / (X2 - X1) -12 - (-5) / 8 - 6 = -7 / 2 La pente est -7/2 (du premier point au deuxième on descend 7 vers le bas et 2 vers la droite, donc la pente est de -7 sur 2). Réorganisez votre équation. b = y - mx. Entrez les valeurs et résolvez. b = -12 - (-7/2)8. b = -12 - (-28). b = -12 + 28. b = 16 Remarque: parce que nous avons utilisé le 8 pour les coordonnées, nous devons également utiliser le -12.Si vous utilisez le 6 pour vos coordonnées, vous devez également utiliser le -5. Vérifiez que votre intersection avec l`axe des y est bien 16. Écrivez l`équation : y = -7/2 x + 16 
Remplacez la pente et les coordonnées dans l`équation ci-dessus. Multipliez la pente (m) avec l`abscisse du point. Soustraire la valeur de la coordonnée y du point. Vous avez b résolu, l`intersection avec l`axe des y. 


Résoudre la pente. La pente de notre nouvelle ligne sera la même que la pente de l`ancienne ligne. Déterminer la pente de l`ancienne droite : -2y = -5x + 1 tirer "-2" off des deux côtés : y = 5/2x - 1/2 La pente est 5/2. Réorganisez votre équation. b = y - mx. Remplissez et résolvez. b = 3 - (5/2)4. b = 3 - (10). b = -7. Vérifiez si l`intersection avec l`axe des y est vraiment -7. Écrivez l`équation : y = 5/2 x - 7 
2/3 devient -3/2 -6/5 devient 5/6 3 (ou 3/1 — c`est le même) devient -1/3 -1/2 devient 2 
Branchez votre pente et vos coordonnées dans l`équation ci-dessus. Multipliez la pente (m) avec l`abscisse du point. Soustraire cette valeur de la coordonnée y du point. Vous avez maintenant résolu l`équation de b; l`intersection avec l`axe des y. 


Résoudre la pente. La pente de notre nouvelle ligne devient l`inverse négatif de la pente de l`ancienne ligne. Déterminer la pente de l`ancienne droite : 2y = -4x + 9 tirer "2" off des deux côtés : y = -4/2x + 9/2 La pente est -4/2 ou -2. L`inverse négatif de -2 est 1/2. réorganise ton équation. b = y - mx. Remplissez et résolvez. b = -1 - (1/2)8. b = -1 - (4). b = -5. Vérifiez que votre intersection avec l`axe des y est bien -5. Écrivez l`équation : y = 1/2 x - 5
Trouver l'équation d'une droite
Teneur
Pour trouver l`équation d`une droite que vous avez besoin de deux choses:a) un point sur la ligne ; et b) la pente (parfois aussi la pente) de la ligne. Mais la manière dont vous collectez ces deux informations et ce que vous en faites par la suite peut être très différente selon la situation. Par souci de simplicité, cet article se concentrera sur les équations de la forme y = mx + b à la place de (y - oui1) = m(x - x1).
Pas
Méthode 1 sur 5 : Informations générales
1. Savoir quoi chercher.Avant de pouvoir rechercher la comparaison, vous devez savoir avec certitude ce que vous essayez de trouver. Gardez ce qui suit à l`esprit :
- Les points sont classés comme paire ordonnée, comme (-7, -8) ou (-2,-6).
- Le premier nombre d`une paire ordonnée est le x coordonnée. C`est la position horizontale du point (combien d`unités à gauche ou à droite de l`origine).
- Le deuxième nombre d`une paire ordonnée est le y coordonner. C`est la position verticale du point (combien d`unités vers le haut ou vers le bas depuis l`origine).
- le pente entre les deux points est appelé le "la pente" — en d`autres termes, jusqu`où vous devez monter (ou descendre) et à droite (ou à gauche) pour aller d`un point à un autre.
- Deux lignes sont parallèle s`ils ne se croisent pas.
- Deux lignes sont perpendiculaires les uns aux autres s`ils se coupent à angle droit (90 degrés).
2. Déterminez à quel type de mission vous avez affaire.
3. Résoudre le problème en utilisant l`une des quatre méthodes ci-dessous. Selon les informations fournies, il existe différentes manières de le résoudre.
Méthode 2 sur 5:Un point et une pente sont donnés

1. Trouvez l`intersection de votre équation avec l`axe des y. L`intersection avec l`axe des y (ou la variable b dans notre équation) est le point d`intersection de la ligne avec l`axe des y. Vous pouvez calculer l`intersection avec l`axe des y en réorganisant l`équation à résoudre pour b. Notre nouvelle équation ressemble maintenant à ceci : b = y - mx.
- Entrez votre pente et vos coordonnées dans l`équation ci-dessus.
- Multipliez la pente (m) avec l`abscisse du point.
- Soustraire cette valeur de la coordonnée y du point.
- Maintenant vous avez b résolu, l`intersection avec l`axe des y.

2. Écrivez la formule :y = ____ x + ____ , avec les blancs.

3. Remplissez le premier espace vide, celui du x, avec la pente.

4. Remplissez le deuxième blanc avec l`intersection avec l`axe des y que vous avez calculé avant.

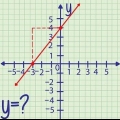
5. Résoudre le problème de l`exemple. "Étant donné le point (6, -5) et la pente 2/3, quelle est l`équation de la droite?"
Méthode 3 sur 5:Deux points sont donnés
1. Calculer la pente entre deux points. La pente est aussi appelée la pente et vous pouvez considérer cela comme la vitesse à laquelle quelque chose se déplace le long d`un axe y et d`un axe x imaginaires. L`équation de la pente est : (Y2 - Oui1) / (X2 - X1)
- Prenez les deux points et utilisez-les dans l`équation (deux coordonnées signifient deux oui-valeurs et deux X-valeurs). Peu importe les coordonnées que vous entrez en premier, tant que vous le faites de manière cohérente. Quelques exemples:
- Points (3, 8) et (7, 12). (Oui2 - Oui1) / (X2 - X1) = 12 - 8 / 7 - 3 = 4/4, ou 1.
- Points (5, 5) et (9, 2). (Oui2 - Oui1) / (X2 - X1) = 2 - 5 / 9 - 5 = -3/4.

2. Choisissez un ensemble de coordonnées pour le reste du problème. Rayez ou couvrez l`autre ensemble de coordonnées afin de ne pas les utiliser accidentellement.

3. Calculez l`intersection avec l`axe des y de votre équation. Encore une fois, réorganisez la formule y = mx + b pour obtenir une équation de la forme b = y – mx. C`est toujours la même équation; tu viens de le réarranger.

4. Écrivez la formule :y = ____ x + ____ , y compris les blancs.

5. Remplissez le premier espace vide, celui du x, avec la pente.

6. Remplissez le deuxième blanc avec l`intersection avec l`axe des y.

sept. Résoudre le problème de l`exemple. "Étant donné les points (6, -5) et (8, -12), quelle est l`équation de la droite?"
Méthode 4 sur 5: Lorsqu`un point et une ligne parallèle sont donnés
1. Déterminer la pente de la droite parallèle. Rappelez-vous que la pente est le coefficient de X par lequel oui n`a pas de coefficient.
- Dans une équation telle que y = 3/4 x + 7, la pente est de 3/4.
- Dans une équation telle que y = 3x - 2, la pente est de 3.
- Dans une équation telle que y = 3x, la pente est toujours de 3.
- Dans une équation telle que y = 7, la pente est nulle (car il y a zéro x dans le problème).
- Dans une équation telle que y = x - 7, la pente est 1.
- Dans une équation telle que -3x + 4y = 8, la pente est de 3/4.
- Pour trouver la pente d`une équation comme celle-ci, il suffit de la réarranger de sorte que le oui est isolé :
- 4y = 3x + 8
- Divisez les deux côtés par 4 : y = 3/4x + 2

2. Calculer l`intersection avec l`axe des y, en utilisant la pente de la première étape et l`équation b = y - mx.

3. Écrivez la formule :y = ____ x + ____ , avec les blancs.

4. Remplissez le premier espace vide, avant le x, avec la pente que vous avez déterminée à l`étape 1.Ce qui est remarquable avec les lignes parallèles, c`est qu`elles ont la même pente, donc vous vous retrouvez avec ce avec quoi vous avez commencé.

5. Remplissez l`intersection avec l`axe des y dans le deuxième espace vide.
6. Résoudre le problème de l`exemple. "Étant donné le point (4, 3) et la droite parallèle 5x - 2y = 1 ; quelle est l`équation de la droite?"
Méthode 5 sur 5: Avec un point donné et une ligne perpendiculaire
1. Trouver la pente de la droite donnée. Consultez les exemples ci-dessus pour plus d`informations.

2. Trouver l`inverse négatif de cette pente. En d`autres termes, retournez-le et changez le signe. Le point avec les lignes perpendiculaires est qu`elles ont une pente inverse négative, vous devrez donc apporter des modifications à la pente avant de pouvoir l`utiliser.

3. Calculer l`intersection avec l`axe des y en utilisant la pente à partir de l`étape 2 et l`équation b = y - mx

4. Écrivez la formule :y = ____ x + ____ , avec les blancs.

5. Remplissez le premier espace vide, avant le x, avec la pente que vous avez calculée à l`étape 2.

6. Remplissez l`intersection avec l`axe des y dans le deuxième espace vide.
sept. Résoudre le problème de l`exemple. "Soit (8, -1) et et la perpendiculaire 4x + 2y = 9 ; quelle est l`équation de la droite?"
Articles sur le sujet "Trouver l'équation d'une droite"
Оцените, пожалуйста статью
Populaire