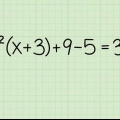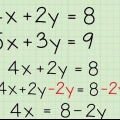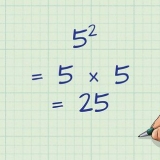Résolution d'une équation cubique

Teneur

La première fois que vous rencontrez une équation cubique (de la forme hache + bx + cx + ré=0) cela peut sembler presque insoluble. Cependant, cette méthode de résolution des équations cubiques existe depuis des siècles! Il a été découvert au 16ème siècle par les mathématiciens italiens Niccolò Tartaglia et Gerolamo Cardano. C`était l`une des premières formules inconnues des anciens Grecs et Romains. Résoudre des équations cubiques peut être très difficile, mais avec la bonne approche (et suffisamment de connaissances de base), même les équations cubiques les plus délicates peuvent être apprivoisées.

Pas

Méthode 1 sur 3: Résoudre avec la formule abc

Image intitulée Résoudre une équation cubique Étape 1

1. Vérifiez si l`équation cubique contient une constante. Comme indiqué ci-dessus, les équations cubiques ont la forme hache + bx + cx + ré=0. avant JC, et ré peut être 0 sans changer s`il s`agit ou non d`une équation cubique - ce qui signifie essentiellement qu`une équation ne doit pas nécessairement être constituée de tous les termes bx, cx ou ré être une équation cubique. Vous commencez à appliquer cette méthode relativement simple de résolution d`équations cubiques en vérifiant d`abord si votre équation a une constante (un ré-où le). Est-ce pas le cas, alors vous pouvez de formule abc pour trouver les réponses de l`équation avec un peu de maths.

Si l`équation contient une constante, vous devrez utiliser une méthode différente. Voir ci-dessous pour des approches alternatives.

Image intitulée Résoudre une équation cubique Étape 2

2. dissoudre un X hors de l`équation. Puisque votre équation ne contient pas de constante, chaque terme de l`équation a un X-variable. Cela signifie qu`un X peut être pris en compte hors de l`équation pour la simplifier. Faites ceci et réécrivez votre équation sous la forme X(hache + bx + c).

Par exemple, supposons que vous ayez l`équation 3X + -2X + 14X=0. Par un X en dehors des parenthèses, on obtient X(3X + -2X + 14)=0.

Image intitulée Résoudre une équation cubique Étape 3

3. Utilisez la formule abc pour résoudre les termes entre parenthèses. Vous avez peut-être remarqué que les termes de votre nouvelle équation entre parenthèses se présentent sous la forme d`une équation quadratique (hache + bx + c). Cela signifie que nous pouvons trouver les valeurs pour lesquelles l`équation quadratique est égale à zéro par un B et c dans la formule abc ({-b +/-√ (b- 4ca)}/2une). Cela trouvera deux des réponses de votre équation cubique.

Dans notre exemple de déclaration, nous remplissons nos valeurs un B et c (respectivement 3, -2 et 14) dans l`équation quadratique en :

{-b +/-√ (b- 4ca)}/2une

{-(-2) +/-√ ((-2)-4(3)(14))}/2(3)

{2 +/-√ (4 - (12)(14))}/6

{2 +/-√ (4 - (168))}/6

{2 +/-√ (-164)}/6

Réponse 1:

{2 + (-164)}/6

{2 + 12.8je}/6

Réponse 2 :

{2 - 12.8je}/6

Image intitulée Résoudre une équation cubique Étape 4

4. Utilisez zéro et les réponses quadratiques comme réponses à votre équation cubique. Les équations quadrilatérales ont deux solutions, mais les équations cubiques en ont trois. Vous en avez déjà deux - ce sont les réponses que vous avez trouvées en travaillant l`"équation quadratique" entre parenthèses. Dans les cas où une équation est appropriée pour ce "hors parenthèse", la troisième réponse sera toujours 0 sont. Félicitations, vous venez de résoudre une équation cubique.

La raison pour laquelle cela fonctionne a à voir avec le fait fondamental que tout nombre multiplié par zéro est égal à zéro. Lorsque vous convertissez l`équation sous la forme X(hache + bx + c)=0, vous divisez essentiellement les deux en parties : une partie est le X-variable hors parenthèses et l`autre est le carré entre parenthèses. Si l`une de ces parties est égale à zéro, alors toute l`équation l`est aussi. Donc, si les deux réponses au carré à l`intérieur des parenthèses rendent cette partie nulle, alors les réponses à l`équation cubique rendront également la partie à l`extérieur des parenthèses égale à zéro.

Méthode 2 sur 3: Résolution à l`aide de listes de facteurs

Image intitulée Résoudre une équation cubique Étape 5

1. Assurez-vous que votre équation cubique a une constante. Bien que la méthode ci-dessus soit utile car elle ne vous oblige pas à acquérir de nouvelles compétences en mathématiques, elle ne fonctionnera pas toujours pour résoudre des équations cubiques. Si votre équation est sous la forme hache + bx + cx + ré=0 état, et ré est différent de zéro, les parenthèses ne fonctionneront pas et vous aurez besoin de cette méthode ou de celle de la partie suivante.

Par exemple, supposons que vous ayez l`équation donnée 2X + 9X + 13X=-6. Dans ce cas, un 0 à droite du signe égal nécessitera d`ajouter 6 des deux côtés. Notre nouvelle équation est 2X + 9X + 13X + 6=0, ré=6, donc on ne peut pas utiliser les parenthèses de la partie précédente.

Image intitulée Résoudre une équation cubique Étape 6

2. Déterminer les facteurs de une et ré. Pour résoudre l`équation cubique, commencez par déterminer les facteurs de une (le coefficient de la X termes ré (la constante à la fin de l`équation). Pour rappel, les facteurs sont ces nombres qui se sont multipliés pour former un autre nombre. Par exemple, parce que votre 6 résulte de la multiplication 6 &temps; 1 et 2 × 3, sont 1, 2, 3 et 6 facteurs de 6.

Dans notre exemple de déclaration, une=2 et d=6. Les facteurs de 2 sont 1 et 2. Les facteurs de 6 sont 1, 2, 3 et 6.

Image intitulée Résoudre une équation cubique Étape 7

3. Partager les facteurs de une par les facteurs de ré. Maintenant, vous listez toutes les valeurs que vous obtenez en divisant chaque facteur une par n`importe quel facteur ré. Cela se traduit généralement par de nombreuses fractions et quelques nombres entiers. Les solutions entières de votre équation cubique seront soit l`un des entiers de la liste, soit le nombre négatif de l`un de ces nombres.

Dans notre équation, vous calculez les facteurs de une (1, 2) sur les facteurs de ré (1, 2, 3, 6) et vous obtenez la liste suivante : 1, 1/2, 1/3, 1/6, 2 et 2/3. Ajoutons maintenant les nombres négatifs à la liste pour la compléter : 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3 et -2/3. La solution entière de notre équation cubique peut être trouvée quelque part dans cette liste.

Image intitulée Résoudre une équation cubique Étape 8

4. Utilisez le partage synthétique pour vérifier manuellement vos réponses. Une fois que vous avez compilé la liste des valeurs, vous pouvez trouver les solutions entières de votre équation cubique en saisissant rapidement et manuellement chaque entier et en vérifiant lesquelles sont égales à zéro. Si vous ne voulez pas passer du temps là-dessus, il existe une méthode légèrement plus rapide selon une technique appelée partage synthétique. L`essentiel est que vous divisez les nombres entiers par l`original a, b, c et ré coefficients de votre équation cubique. S`il vous reste un reste de 0, votre valeur est l`une des solutions de l`équation cubique.

Le partage synthétique est un sujet complexe — suivez le lien ci-dessus pour plus d`informations. Voici un exemple de recherche d`une des solutions de notre équation cubique en utilisant la division synthétique :

-1 | 2 9 13 6

__| -2-7-6

__| 2 7 6 0

Puisque nous nous retrouvons avec un 0 comme reste, nous savons que l`une des solutions de notre équation cubique est l`entier -1 est.

Méthode 3 sur 3: Utilisation du « discriminant »

Image intitulée Résoudre une équation cubique Étape 9

1. Écrivez les valeurs de a, b, c et ré. Dans cette méthode pour trouver les solutions d`une équation cubique, nous nous appuierons fortement sur les coefficients des termes de notre équation. Pour cette raison, il est sage d`utiliser les termes a, b, c et ré notez-le avant de commencer pour ne pas oublier ce que chacun est.

Par exemple, pour la comparaison X - 3X + 3X - 1, nous écrivons une=1, b=-3, c=3 et ré=-1. N`oubliez pas celui d`un X-variable sans coefficient on suppose que le coefficient est égal à 1.

Image intitulée Résoudre une équation cubique Étape 10

2. Calculer 0=b - 3ca. Lorsque vous utilisez le discriminant pour résoudre des équations cubiques, vous avez besoin d`un peu plus de mathématiques avancées, mais si vous suivez attentivement la procédure, vous constaterez qu`il s`agit d`un outil précieux pour résoudre ces équations cubiques déjà délicates. Commencez par trouver 0, la première de plusieurs valeurs importantes dont nous avons besoin, en substituant les valeurs appropriées dans la formule b - 3ca.

Dans notre exemple de problème, nous le résolvons comme suit :

b - 3ca

(-3) - 3(1)(3)

9 - 3(1)(3)

9 - 9=0=Δ0

Image intitulée Résoudre une équation cubique Étape 11

3. Calculer 1=2b - 9abc + 27uneré. La prochaine quantité importante dont nous avons besoin, 1, nécessite un peu plus de travail, mais peut être trouvée de la même manière que Δ0. Remplacez les valeurs correctes dans la formule 2b - 9abc + 27uneré pour la valeur de 1.

Dans notre exemple de problème, nous le résolvons comme suit :

2(-3) - 9(1)(-3)(3) + 27(1)(-1)

2(-27) - 9(-9) + 27(-1)

-54 + 81 - 27

81 - 81=0=Δ1

Image intitulée Résoudre une équation cubique Étape 12

4. Calculer Δ=Δ1 - 4Δ0) ÷ -27une. Ensuite, nous calculons le discriminant de l`équation cubique à partir des valeurs de Δ0 et Δ1. Un discriminant est simplement un nombre qui nous dit quelque chose sur les réponses d`un polynôme (inconsciemment, vous connaissez peut-être déjà le discriminant quadratique : b - 4ca). Dans le cas de l`équation cubique, si le discriminant est positif, alors l`équation a trois solutions réelles. Si le discriminant est nul, alors l`équation a une ou deux solutions réelles, et certaines de ces solutions sont partagées. Si elle est négative, alors l`équation n`a qu`une seule solution. (Une équation cubique a toujours une solution réelle, car le graphique est toujours au moins une fois avec le X-coupes d`axe.)

Dans notre exemple de problème, déterminer est très simple, car Δ0 et Δ1=0. Nous résolvons cela comme suit :

1 - 4Δ0) ÷ -27une

(0) - 4(0)) -27(1)

0 - 0 27

0=Δ, donc notre équation a 1 ou 2 réponses.

Image intitulée Résoudre une équation cubique Étape 13

5. calculer C=√(√((Δ1 - 4Δ0) + Δ1)/ 2). La dernière valeur importante à calculer est C. Avec cette quantité importante, on peut enfin trouver les trois solutions. Résolvez ceci comme d`habitude, en remplaçant Δ1 et Δ0 si nécessaire.

Dans notre exemple de problème, nous trouvons C comme suit:

(√((Δ1 - 4Δ0) + Δ1)/ 2)

(√((0 - 4(0)) + (0))/ 2)

(√((0 - 0) + (0))/ 2)

0=C

Image intitulée Résoudre une équation cubique Étape 14

6. Calculez les trois réponses avec vos variables. Les réponses à votre équation cubique sont données par la formule (b + uC + (Δ0/uC)) / 3une, par lequel vous=(-1 + (-3))/2 et m est 1, 2 ou 3. Entrez vos valeurs si nécessaire pour résoudre ce problème - cela nécessite beaucoup de mathématiques, mais devrait vous donner trois réponses possibles!

Dans notre exemple de problème, nous pouvons résoudre ce problème en vérifiant la réponse lorsque n est égal à 1, 2 ou 3. Les réponses que nous obtenons de ces tests sont les réponses possibles à notre équation cubique - toute solution qui donne 0 après substitution dans l`équation est correcte. Par exemple, supposons que nous obtenions 1 en réponse à l`un des tests, car entrer 1 dans X - 3X + 3X - 1 donne 0 si réponse, alors 1 une des réponses à notre équation cubique.