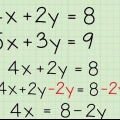2x - 2x = 0 4 ans - 2 ans = 2 ans 8 - 2 = 6 2x + 4y = 8-(2x + 2y = 2)=0 +2y = 6 
2 ans = 6 Divisez 2y et 6 par 2 et obtenez y = 3 
Insérez y = 3 dans l`équation 2x + 2y = 2 et résolvez pour x. 2x + 2(3) = 2 2x + 6 = 2 2x = -4 x = - 2 Vous avez résolu le système d`équations par soustraction. (x, y) = (-2, 3) 
Remplissez (-2, 3) pour (x, y) dans l`équation 2x + 4y = 8. 2(-2) + 4(3) = 8 -4 + 12 = 8 8 = 8 Remplissez (-2, 3) pour (x, y) dans l`équation 2x + 2y = 2. 2(-2) + 2(3) = 2 -4 + 6 = 2 2 = 2 

3x + x = 4x 6a + -6a = 0 8 + 4 = 12 Si vous combinez cela, vous obtenez un nouveau produit : 3x + 6y = 8 +(x - 6y = 4) = 4x + 0 = 12 
4x + 0 = 12 4x = 12 Divisez 4x et 12 par 3 pour obtenir x = 3 
Branchez x = 3 dans l`équation x - 6y = 4 pour trouver y. 3 - 6 ans = 4 -6y = 1 Divisez -6y et 1 par -6 pour obtenir y = -1/6. Vous avez résolu le système d`équations avec l`addition. (x, y) = (3, -1/6) 
Remplissez (3, -1/6) pour (x, y) dans l`équation 3x + 6y = 8. 3(3) + 6(-1/6) = 8 9 - 1 = 8 8 = 8 Remplissez (3, -1/6) pour (x, y) dans l`équation x - 6y = 4. 3 - (6 * -1/6) =4 3 - - 1 = 4 3 + 1 = 4 4 = 4 

2 (2x - y = 2) 4x - 2y = 4 
3x + 2y = 10 + 4x - 2y = 4 7x + 0 = 14 7x = 14 

x = 2 ---> 2x - y = 2 4 - y = 2 -y = -2 y = 2 Vous avez résolu le système d`équations en utilisant la multiplication. (x, y) = (2, 2) 
Remplissez (2, 2) pour (x, y) dans l`équation 3x + 2y = 10. 3(2) + 2(2) = 10 6 + 4 = 10 10 = 10 Remplissez (2, 2) pour (x, y) dans l`équation 2x - y = 2. 2(2) - 2 = 2 4 - 2 = 2 2 = 2 

x = 2 - 4 ans --> 2x + 3y = 9 2(2 - 4 ans) + 3 ans = 9 4 - 8 ans + 3 ans = 9 4 - 5 ans = 9 -5y = 9 - 4 -5 ans = 5 -y = 1 y = - 1 
y = -1 --> x = 2 - 4 ans x = 2 - 4(-1) x = 2 - -4 x = 2 + 4 x = 6 Vous avez résolu le système d`équations en utilisant la substitution. (x, y) = (6, -1) 
Remplissez (6, -1) pour (x, y) dans l`équation 2x + 3y = 9. 2(6) + 3(-1) = 9 12 - 3 = 9 9 = 9 Remplissez (6, -1) pour (x, y) dans l`équation x + 4y = 2. 6 + 4(-1) = 2 6 - 4 = 2 2 = 2
Résoudre un système d'équations
Teneur
Résoudre un système d`équations nécessite de trouver la valeur de plusieurs variables dans plusieurs équations. Vous pouvez résoudre un système d`équations en utilisant l`addition, la soustraction, la multiplication ou la substitution. Si vous souhaitez apprendre à résoudre un système d`équations, il vous suffit de suivre ces étapes.
Pas
Méthode 1 sur 4: Résoudre par soustraction

1. Écrire une équation sur l`autre. Résoudre ces équations par soustraction est une méthode idéale si vous voyez que les deux équations ont la même variable avec le même coefficient et le même signe. Par exemple, si les deux équations ont la variable -2x, vous pouvez utiliser la soustraction pour trouver la valeur des deux variables.
- Écrivez une équation au-dessus de l`autre de sorte que les variables x et y des deux équations et les nombres soient en dessous les uns des autres. Placez le signe moins à côté du chiffre du bas.
- Ex : Si vous avez les deux équations suivantes : 2x + 4y = 8 et 2x + 2y = 2, cela ressemblerait à ceci :
- 2x + 4y = 8
- -(2x + 2y = 2)

2. Soustraire des termes similaires. Maintenant que les deux équations sont alignées, il ne vous reste plus qu`à soustraire les termes similaires. Faites cela avec un terme à la fois :

3. Résoudre pour le terme restant. Supprimez tout zéro de l`équation qui a été créée, cela ne change pas la valeur et résolvez l`équation restante.

4. Entrez la valeur trouvée de la variable dans l`une des équations. Maintenant que vous savez que y = 3, vous pouvez insérer cette valeur dans l`équation d`origine pour résoudre x. Quelle que soit l`équation choisie, la réponse est la même. Alors utilise l`équation la plus simple!

5. Vérifie ta réponse. Pour vous assurer que votre réponse est correcte, entrez les deux réponses dans les deux équations. Voici comment procéder :
Méthode 2 sur 4: Résoudre par addition

1. Écrire une équation sur l`autre. Résoudre un système d`équations par addition est la meilleure méthode, si vous remarquez que les deux équations ont une variable avec le même coefficient, mais avec un signe différent ; par exemple, si une équation contient la variable 3x et l`autre la variable -3x.
- Écrivez une équation au-dessus de l`autre de sorte que les variables x et y des deux équations et les nombres soient en dessous les uns des autres. Placez le signe plus à côté du numéro du bas.
- Ex : Vous avez les deux équations suivantes 3x + 6y = 8 et x - 6y = 4, puis écrivez la première équation au-dessus de la seconde comme indiqué ci-dessous :
- 3x + 6y = 8
- +(x - 6y = 4)

2. Ajouter des termes similaires ensemble. Maintenant que les deux équations sont alignées l`une au-dessus de l`autre, il ne vous reste plus qu`à additionner les termes ayant la même variable :

3. Résoudre pour le terme restant. Supprimez tout zéro de l`équation qui s`est produite, cela ne change pas la valeur. Résoudre l`équation restante.

4. Entrez la valeur trouvée de cette variable dans l`une des équations. Maintenant que vous savez que x = 3, vous pouvez insérer cette valeur dans l`équation d`origine pour résoudre y. Quelle que soit l`équation choisie, la réponse est la même. Alors utilise l`équation la plus simple!

5. Vérifie ta réponse. Pour vous assurer que votre réponse est correcte, entrez les deux réponses dans les deux équations. Voici comment procéder :
Méthode 3 sur 4: Résoudre par multiplication

1. Écrire une équation sur l`autre. Écrivez une équation au-dessus de l`autre de sorte que les variables x et y des deux équations et les nombres soient en dessous les uns des autres. Si vous utilisez la multiplication, vous le faites parce qu`aucune des variables n`a de coefficients égaux - pour le moment.
- 3x + 2y = 10
- 2x - y = 2

2. Assurer des coefficients égaux. Multipliez ensuite une ou les deux équations par un nombre, de sorte que l`une des variables ait le même coefficient. Dans ce cas, vous pouvez multiplier toute la deuxième équation par 2 pour que -y soit égal à -2y et donc au premier coefficient y. Voici comment procéder :

3. Additionner ou soustraire les équations. Il ne vous reste plus qu`à éliminer les termes égaux en ajoutant ou en soustrayant. Puisque vous avez affaire à 2y et -2y ici, il est logique d`utiliser la méthode d`addition car elle est égale à 0. Si vous avez affaire à 2 ans + 2 ans, utilisez la méthode de soustraction. Voici un exemple d`utilisation de la méthode d`addition pour éliminer des variables :

4. Résoudre ceci pour le terme restant. Ceci est facilement résolu en trouvant la valeur du terme que vous n`avez pas encore éliminé. Si 7x = 14, alors x = 2.

5. Entrez la valeur trouvée dans l`une des équations. Entrez le terme dans l`une des équations originales à résoudre pour l`autre terme. Choisissez l`équation la plus simple pour cela, c`est la plus rapide.

6. Vérifie ta réponse. Pour vous assurer que votre réponse est correcte, entrez les deux réponses dans les deux équations. Voici comment procéder :
Méthode 4 sur 4: Résoudre par substitution

1. Isoler une variable. La substitution est idéale lorsque l`un des coefficients dans l`une des équations est égal à 1. Ensuite, tout ce que vous avez à faire est d`isoler cette variable d`un côté de l`équation pour trouver sa valeur.
- Si vous travaillez avec les équations 2x + 3y = 9 et x + 4y = 2, alors vous devez isoler x dans la deuxième équation.
- x + 4y = 2
- x = 2 - 4 ans

2. Remplissez la valeur de la variable que vous avez isolée dans l`autre équation. Prendre la valeur de la variable isolée et la brancher dans l`autre équation. Bien sur pas dans la même équation sinon tu ne résoudra rien. Voici un exemple de comment procéder :

3. Résoudre pour la variable restante. Maintenant que vous savez que y = - 1, branchez cette valeur dans l`équation plus simple pour trouver la valeur de x. Voici un exemple de la façon de procéder :

4. Vérifie ta réponse. Pour vous assurer que votre réponse est correcte, entrez les deux réponses dans les deux équations. Voici comment procéder :
Des astuces
- Vous devriez maintenant être capable de résoudre n`importe quel système d`équations linéaire en utilisant l`addition, la soustraction, la multiplication ou la substitution, mais une méthode est généralement la plus appropriée en fonction des équations.
Articles sur le sujet "Résoudre un système d'équations"
Оцените, пожалуйста статью
Populaire