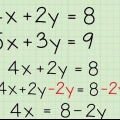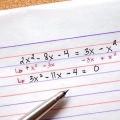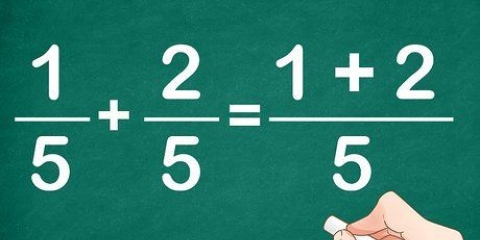La multiplication croisée fonctionne sur des principes algébriques communs. Les expressions rationnelles et autres fractions peuvent être converties en nombres ordinaires en multipliant les dénominateurs. La multiplication croisée est fondamentalement un moyen pratique et abrégé de multiplier les deux côtés de l`équation par les dénominateurs des fractions. Ne le crois-tu pas? Essayez-le - vous verrez les mêmes résultats après avoir simplifié. 
Par exemple, si (x+3)/4 = x/(-2) était votre expression rationnelle d`origine, alors après multiplication croisée, elle devient égale à -2(x+3) = 4x. Cela peut éventuellement être réécrit comme -2x - 6 = 4x. 
Dans notre exemple, il est possible de diviser les deux membres de l`équation par -2, ce qui donne usx+3 = -2x. Soustraire x des deux côtés du signe égal nous donne 3 = -3x. Et enfin, en divisant les deux côtés par -3 on obtient -1 = x, ou encore x = -1. Maintenant, nous avons trouvé x en résolvant notre équation rationnelle. 

Parfois, le plus petit commun multiple - le plus petit nombre qui est divisible par chacun des dénominateurs - est immédiatement apparent. Par exemple, si votre expression ressemble à x/3 + 1/2 = (3x+1)/6, alors il est facile de voir que le lcm doit être divisible par 3, 2 et 6, il est donc égal à 6. Mais le plus souvent, le LCF d`une équation rationnelle n`est pas du tout immédiatement clair. Dans ces cas, essayez les multiples du plus grand dénominateur jusqu`à ce que vous trouviez un nombre qui inclut les multiples des autres plus petits dénominateurs. Souvent, le LCF est le produit de deux dénominateurs. Par exemple, prenons l`équation x/8 + 2/6 = (x - 3)/9, où le lcm est égal à 8*9 = 72. Si un ou plusieurs des dénominateurs contiennent une variable, ce processus est un peu plus difficile, mais il n`est certainement pas impossible. Dans ces cas, le LCF est une expression (avec des variables) dans laquelle tous les dénominateurs s`intègrent complètement, pas seulement un seul nombre. À titre d`exemple, l`équation 5/(x-1) = 1/x + 2/(3x), où le lcm est égal à 3x(x-1), car il est entièrement divisible par n`importe quel dénominateur - en divisant par (x - 1) donne 3x, la division par 3x donne (x-1) et la division par x donne 3(x-1). 
Dans notre exemple, nous pouvons multiplier x/3 par 2/2 pour obtenir 2x/6 et multiplier 1/2 par 3/3 pour obtenir 3/6. 3x +1/6 a déjà un 6 (LCM) comme dénominateur, nous pouvons donc le multiplier par 1/1 ou simplement le laisser tel quel. Dans notre exemple avec des variables dans les dénominateurs, l`ensemble du processus est un peu plus compliqué. Puisque le lcc est égal à 3x(x-1) nous multiplions toute expression rationnelle par une fraction qui donne 3x(x-1) comme dénominateur. On multiplie 5/(x-1) par (3x)/(3x) et cela donne 5(3x)/(3x)(x-1), on multiplie 1/x par 3(x-1)/3(x -1) et cela donne 3(x-1)/3x(x-1) et on multiplie 2/(3x) par (x-1)/(x-1) et cela donne finalement 2(x-1)/ 3x(x-1). 
Dans notre exemple, après multiplication, en misant 1 comme fraction, on obtient 2x/6 + 3/6 = (3x+1)/6. Deux fractions peuvent être additionnées si elles ont le même dénominateur, nous pouvons donc écrire cette équation sous la forme (2x+3)/6 = (3x+1)/6 sans changer sa valeur. Multipliez les deux côtés par 6 pour annuler les dénominateurs, nous laissant avec 2x+3 = 3x+1. Ici, soustrayez 1 des deux côtés pour obtenir 2x+2 = 3x et soustrayez 2x des deux côtés pour obtenir 2 = x, qui peut alors également être écrit sous la forme x = 2. Dans notre exemple avec des variables aux dénominateurs, l`équation après avoir multiplié chaque terme par "1" égal à 5(3x)/(3x)(x-1) = 3(x-1)/3x(x-1) + 2(x-1)/3x(x-1). Multiplier chaque terme par le lcm permet d`éliminer les dénominateurs, ce qui nous donne 5(3x) = 3(x-1) + 2(x-1). Ceci est encore élaboré comme 15x = 3x - 3 + 2x -2, qui peut encore être simplifié comme 15x = x - 5. La soustraction de x des deux côtés donne 14x = -5, ce qui peut simplifier la réponse finale à x = -5/14.
Résoudre des équations avec des fractions
Teneur
Une fonction rationnelle est une fraction avec une ou plusieurs variables au numérateur ou au dénominateur. Une équation rationnelle est une équation qui contient au moins une expression rationnelle. Comme les équations algébriques régulières, les expressions rationnelles peuvent être résolues en appliquant la même opération aux deux côtés de l`équation jusqu`à ce que la variable soit isolée d`un côté du signe égal. Deux méthodes spéciales, la multiplication croisée et la recherche du plus petit commun multiple des dénominateurs, sont particulièrement utiles pour isoler des variables et résoudre des équations rationnelles.
Pas
Méthode 1 sur 2 : Méthode 1 : Multiplication croisée

1. Si nécessaire, réorganisez l`équation pour vous assurer qu`il y a une fraction des deux côtés du signe égal. La multiplication croisée est une méthode rapide pour résoudre des équations rationnelles. Malheureusement, cette méthode ne fonctionne que pour les équations rationnelles qui ont exactement une expression ou fraction rationnelle des deux côtés du signe égal. Si ce n`est pas le cas dans votre équation, alors vous aurez probablement besoin de quelques opérations algébriques pour obtenir les termes au bon endroit. Certaines équations rationnelles ne peuvent pas être si facilement converties sous la forme correcte. Dans ces cas, utilisez les méthodes qui utilisent le plus petit commun multiple des dénominateurs.
- Par exemple, l`équation (x + 3)/4 - x/(-2) = 0 peut facilement être convertie en la forme correcte pour la multiplication croisée en ajoutant x/(-2) aux deux côtés de l`équation, ce qui en fait le résultat ressemble à ceci : (x + 3)/4 = x/(-2).
- N`oubliez pas que les nombres décimaux et entiers peuvent être convertis en fractions en leur donnant comme dénominateur 1. (x + 3)/4 - 2.5 = 5, par exemple peut être réécrit comme (x + 3)/4 = 7.5/1, qui permet d`appliquer la multiplication croisée.

2. Multiplication croisée. La multiplication croisée signifie simplement multiplier le numérateur d`une fraction par le dénominateur de l`autre et vice versa. Multiplier le numérateur de la fraction à gauche du signe égal par la fraction à droite. Répétez avec le numérateur à droite et le dénominateur de la fraction à gauche.

3. Rendre les deux produits égaux. Après la multiplication croisée, il vous reste deux produits. Rendez ces deux termes égaux et simplifiez-les pour laisser les termes les plus simples des deux côtés de l`équation.

4. Résoudre pour la variable. Utiliser des opérations algébriques pour trouver la valeur de la variable dans l`équation. N`oubliez pas que si x apparaît des deux côtés du signe égal, vous devez ajouter ou soustraire un terme x pour vous assurer qu`il n`y a que des termes x d`un côté du signe égal.
Méthode 2 sur 2: Méthode 2: Trouver le plus petit commun multiple (LCM) des dénominateurs

1. Essayez de voir quand trouver le plus petit commun multiple des dénominateurs est évident. Le plus petit commun multiple (LCM) des dénominateurs peut être utilisé pour simplifier des équations rationnelles, permettant de trouver les valeurs de leurs variables. Trouver un LCF est une bonne idée si l`équation rationnelle ne peut pas être facilement réécrite sous une forme où il n`y a qu`une fraction ou une expression rationnelle de chaque côté du signe égal. Pour résoudre des équations rationnelles avec trois termes ou plus, les LCF sont un outil utile. Mais pour résoudre des équations rationnelles avec seulement deux termes, la multiplication croisée est souvent plus rapide.

2. Examiner le dénominateur de chaque fraction. Trouver le plus petit nombre divisible par un dénominateur. C`est le kgv de ton équation.

3. Multipliez chaque fraction de l`équation rationnelle par 1. Multiplier n`importe quel terme par 1 peut sembler inutile, mais il y a une astuce ici. 1 peut être écrit sous forme de fraction – par ex. 2/2 et 3/3. Multipliez chaque fraction de votre équation rationnelle par 1, en écrivant 1 à chaque fois que le nombre ou le terme multiplié par chaque dénominateur pour représenter le lcg sous forme de fraction.

4. Simplifier et résoudre pour x. Maintenant que chaque terme de votre équation rationnelle a le même dénominateur, il est possible de supprimer les dénominateurs de l`équation et de résoudre les numérateurs. Il suffit de multiplier les deux côtés de l`équation par le lcg pour éliminer les dénominateurs de sorte qu`il ne vous reste que les numérateurs. Maintenant, c`est devenu une équation régulière que vous pouvez résoudre pour la variable en l`isolant d`un côté du signe égal.
Des astuces
- Une fois que vous avez trouvé la valeur de la variable, vérifiez votre réponse en insérant cette valeur dans l`équation d`origine. Une fois que vous avez obtenu la bonne valeur de la variable, vous devriez pouvoir simplifier l`équation en un théorème simple et valide, tel que 1 = 1.
- Chaque équation peut être écrite comme une expression rationnelle ; il suffit de le mettre comme numérateur au-dessus du dénominateur 1. Donc l`équation x+3 peut être écrite comme (x+3)/1, les deux ont la même valeur.
Articles sur le sujet "Résoudre des équations avec des fractions"
Оцените, пожалуйста статью
Similaire
Populaire