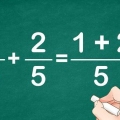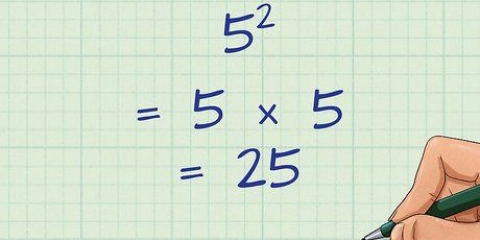Résolution de fractions équivalentes : 8 étapes (avec photos)

Teneur

Pas
- Méthode 1 sur 2: Création de fractions équivalentes
- Méthode 2 sur 2: Résoudre des fractions équivalentes avec des variables
Des astuces
Mises en garde

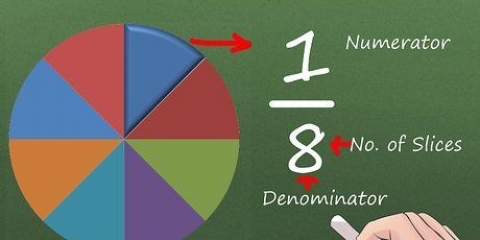
Deux fractions sont "équivalent" s`ils ont la même valeur. Par exemple, les fractions 1/2 et 2/4 sont équivalentes car 1 sur 2 a la même valeur que 2 sur 4 (0,5 sous forme décimale). Savoir convertir une fraction en une autre fraction, mais équivalente, est une valeur mathématique essentielle dont vous avez besoin, de l`algèbre de base aux mathématiques avancées. Regardez l`étape 1 pour commencer!

Pas

Méthode 1 sur 2: Création de fractions équivalentes

$Résoudre des fractions équivalentes$

1. Multipliez le numérateur et le dénominateur d`une fraction par le même nombre pour obtenir une fraction équivalente. Deux fractions différentes mais équivalentes par définition, numérateurs et dénominateurs multiples les uns des autres. En d`autres termes, multiplier le numérateur et le dénominateur d`une fraction par le même nombre produira une fraction équivalente. Même si les nombres de cette nouvelle fraction sont différents, elle a toujours la même valeur.

Par exemple, si nous prenons la fraction 4/8 et multiplions à la fois le numérateur et le dénominateur par 2, nous obtenons (4×2)/(8×2) = 8/16. Ces deux fractions sont équivalentes.

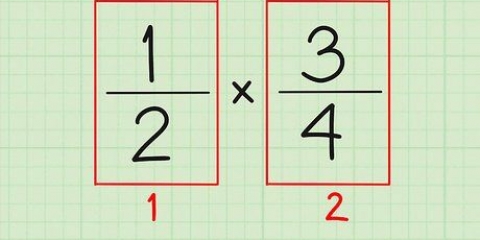
(4×2)/(8×2) est essentiellement la même chose que 4/8 × 2/2 Rappelez-vous que lorsque nous multiplions deux fractions, nous le faisons comme ceci - le numérateur multiplié par le numérateur et le dénominateur multiplié par le dénominateur. Notez que 2/2 est égal à 1. Il est donc facile de comprendre pourquoi 4/8 est égal à 8/16 - la deuxième fraction est la première fraction multipliée par 2!

2. Divisez le numérateur et le dénominateur ou une fraction par le même nombre pour obtenir une fraction équivalente. Comme la multiplication, la division peut également être utilisée pour créer une nouvelle fraction équivalente à la fraction donnée. Divisez simplement le numérateur et le dénominateur d`une fraction par le même nombre pour obtenir une fraction équivalente. Il y a une mise en garde ici - la fraction résultante doit être constituée d`entiers à la fois dans le numérateur et le dénominateur pour être valide.

Par exemple, reprenons 4/8. Si, au lieu de multiplier, on divise à la fois le numérateur et le dénominateur par 2, on obtient (4 2)/(8 2) = 2/4. 2 et 4 sont tous deux des nombres entiers, donc cette fraction équivalente est valide.

$Résoudre des fractions équivalentes$

3. Simplifiez votre fraction en utilisant le plus grand diviseur commun (GGD). Toute fraction donnée a un nombre infini de fractions équivalentes - vous pouvez multiplier le numérateur et le dénominateur par tout entier, grand ou petit pour obtenir une fraction équivalente. Mais la forme la plus simple d`une fraction donnée est généralement celle avec les termes les plus petits. Dans ce cas, le numérateur et le dénominateur sont tous deux aussi petits que possible - ils ne peuvent plus être divisés par un nombre entier pour rendre le terme encore plus petit. Pour simplifier une fraction, nous divisons à la fois le numérateur et le dénominateur par le plus grand diviseur commun.

Le plus grand commun diviseur (GGD) du numérateur et du dénominateur est le plus grand entier par lequel le numérateur et le dénominateur sont divisibles. Donc dans notre exemple 4/8, parce que 4 est le plus grand diviseur de 4 et 8, nous divisons le numérateur et le dénominateur de notre fraction par 4 pour obtenir les termes les plus simples. (4 4)/(8 4) = 1/2.

$Résoudre des fractions équivalentes$

4. Si vous le souhaitez, convertissez les nombres mixtes en fractions impropres pour faciliter la conversion. Bien sûr, toutes les fractions que vous rencontrerez ne seront pas aussi faciles à simplifier que 4/8. Par exemple, les nombres mixtes (par exemple. 1 3/4, 2 5/8, 5 2/3, etc.) peut rendre cette conversion un peu plus difficile. Si vous voulez faire une fraction d`un nombre fractionnaire, vous pouvez le faire de deux manières : faites du nombre fractionnaire une fraction impropre, puis continuez, ou garder le nombre mixte et donner un nombre mixte comme réponse.

Pour convertir une fraction impropre, multipliez l`entier du nombre fractionnaire par le dénominateur de la fraction, puis ajoutez le produit au numérateur. Par exemple, 1 2/3 = ((1 × 3) + 2)/3 = 5/3. Ensuite, vous pouvez le convertir à nouveau si nécessaire. Par exemple, 5/3 × 2/2 = 10/6, toujours le même que 1 2/3.

Cependant, la conversion d`une fraction impropre n`est pas nécessaire. Nous pouvons ignorer l`entier et simplement convertir la fraction, puis y ajouter l`entier. Par exemple, à 3 4/16, nous ne regardons que 4/16. 4/16 4/4 = 1/4. Alors maintenant, nous ajoutons à nouveau l`entier et obtenons un nouveau nombre mixte, 3 1/4.

5. Ne jamais ajouter ou soustraire pour obtenir des fractions équivalentes. Lors de la conversion de fractions en leur forme équivalente, il est important de se rappeler que les seules opérations que vous appliquez sont la multiplication et la division. Ne jamais utiliser d`addition ou de soustraction. La multiplication et la division fonctionnent pour obtenir des fractions équivalentes car ces opérations sont en fait des formes du nombre 1 (2/2, 3/3, etc.) et donnez des réponses qui sont égales à la fraction avec laquelle vous avez commencé. L`addition et la soustraction n`ont pas cette capacité.

Par exemple, ci-dessus, nous avons trouvé que 4/8 ÷ 4/4 = 1/2 . Si nous avions ajouté 4/4 à cela, nous aurions obtenu une réponse complètement différente. 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 ou 3/2, et aucun de ceux-ci n`est égal à 4/8.

Méthode 2 sur 2: Résoudre des fractions équivalentes avec des variables

1. Utiliser la multiplication croisée pour résoudre des problèmes d`équivalence de fraction. Un type délicat de problème d`algèbre traitant des fractions équivalentes implique des équations à deux fractions, où l`une ou les deux contiennent une variable. Dans des cas comme celui-ci, nous savons que ces fractions sont équivalentes car ce sont les seuls termes de chaque côté du signe égal d`une équation, mais il n`est pas toujours évident de résoudre la variable. Heureusement, on peut multiplier par croix, résoudre ce type de problème sans aucun problème.

La multiplication croisée est exactement ce que cela ressemble - vous multipliez de manière croisée sur le signe égal. En d`autres termes, vous multipliez le numérateur d`une fraction par le dénominateur de l`autre fraction et vice versa. Ensuite, vous résolvez l`équation plus loin.
Par exemple, nous avons l`équation 2/x = 10/13. Multipliez maintenant : multipliez 2 par 13 et 10 par x, et approfondissez l`équation :

2×13 = 26
10 × x = 10 x
10x = 26. Maintenant, nous développons l`équation plus loin. x = 26/10 = 2.6

2. Utilisez la multiplication croisée de la même manière que les équations multivariées ou les expressions de variables. L`une des meilleures caractéristiques de la multiplication croisée est qu`elle fonctionne à peu près de la même manière, que vous ayez affaire à deux fractions simples ou complexes. Par exemple, si les deux fractions contiennent des variables, alors rien ne changera - vous n`aurez qu`à vous débarrasser de ces variables. De même, si les numérateurs ou les dénominateurs de votre variable de fraction contiennent des expressions, il suffit "continuer à se multiplier" en utilisant la propriété distributive et en résolvant comme vous le faites habituellement.

Par exemple, supposons que nous ayons l`équation ((x + 3)/2) = ((x + 1)/4). Dans ce cas, nous résolvons cela par multiplication croisée :

(x + 3) × 4 = 4x + 12

(x + 1) × 2 = 2x + 2

2x + 2 = 4x + 12

2 = 2x + 12

-10 = 2x

-5 = x

3. Utiliser des techniques pour résoudre des polynômes. La multiplication croisée ne fonctionne pas toujours un résultat que vous pouvez résoudre avec une algèbre simple. Si vous avez affaire à des termes variables, vous obtiendrez rapidement une équation quadratique ou un autre polynôme en conséquence. Dans de tels cas, vous utilisez, par exemple, la quadrature et/ou la formule carrée.

Par exemple, nous prenons l`équation ((x +1)/3) = (4/(2x - 2)). Première croix multipliez:

(x + 1) × (2x - 2) = 2x + 2x -2x - 2 = 2x - 2

4×3 = 12

2x - 2 = 12. À ce stade, nous voulons convertir cela en une équation quadratique (ax + bx + c = 0) en soustrayant 12 des deux côtés, ce qui donne 2x - 14 = 0. Maintenant, nous utilisons la formule (x = (-b +/- (b - 4ac))/2a) pour trouver la valeur de x :

x = (-b +/- (b - 4ac))/2a. Dans notre équation, 2x - 14 = 0, a = 2, b = 0 et c = -14.

x = (-0 +/- √(0 - 4(2)(-14))))/2(2)

x = (+/- ( 0 - -112))/2(2)

x = (+/- (112))/2(2)

x = (+/- 10.58/4)

x = +/- 2.64 À ce stade, nous vérifions notre réponse en substituant 2,64 et -2,64 dans l`équation quadratique d`origine.

Des astuces

Convertir des fractions en une forme équivalente revient en fait à multiplier par une fraction comme 2/2 ou 5/5. Puisqu`il est finalement égal à 1, la valeur de la fraction reste la même.