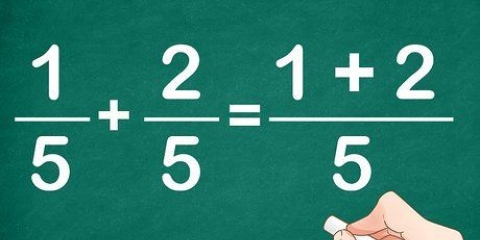Simplifier les fractions mathématiques

Teneur

Pas
Des astuces
Mises en garde

Les fractions mathématiques ou algébriques semblent incroyablement difficiles au début et peuvent sembler intimidantes pour l`étudiant non formé à aborder. Avec un mélange de variables, de nombres et même d`exposants, il est difficile de savoir par où commencer. Mais heureusement, les mêmes règles nécessaires pour simplifier les fractions courantes, telles que 15/25, s`appliquent également aux fractions mathématiques.

Pas

Méthode 1 sur 3: Simplifier les fractions

$Image intitulée Simplifier les fractions algébriques Étape 1$

1. Connaître le vocabulaire des fractions mathématiques. Les termes suivants seront utilisés dans les exemples et sont courants dans les problèmes de fractions :

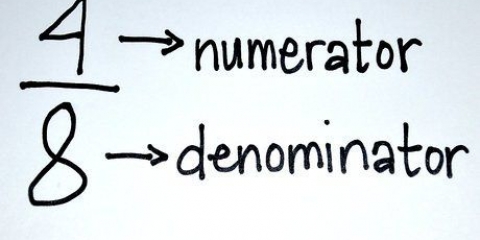
Compteur: La partie supérieure d`une fraction (par exemple. (x+5)/(2x+3)).
Dénominateur: La partie inférieure d`une fraction (par exemple. (x+5)/(2x+3)).
Dénominateur commun: Il s`agit d`un nombre par lequel vous pouvez diviser à la fois le numérateur et le dénominateur d`une fraction. Par exemple, dans la fraction 3/9, le diviseur commun est 3, puisque les deux nombres peuvent être divisés par 3.
Facteur:` Un nombre qui est multiplié pour faire un autre nombre. Par exemple : les facteurs de 15 sont 1, 3, 5 et 15. Les facteurs de 4 sont 1, 2 et 4.
Équation simplifiée : Tous les facteurs communs sont supprimés et les variables égales sont regroupées (5x + x = 6x) jusqu`à ce que vous ayez obtenu la forme la plus simple d`une fraction, d`une équation ou d`un problème. Si tu ne peux plus rien faire avec la fraction, c`est simplifié.

$Image intitulée Simplifier les fractions algébriques, étape 2$

2. Comparez comment résoudre des fractions simples. Ce sont exactement les mêmes étapes que vous suivrez pour résoudre des fractions mathématiques. Prenons l`exemple, 15/35. Pour simplifier une fraction, il faut trouver un dénominateur commun. Dans ce cas, les deux nombres peuvent être divisés par cinq, vous pouvez donc rayer le 5 de la fraction :
15→5 * 3
35→5 *7
Maintenant vous pouvez rayer les mêmes termes. Dans ce cas, vous pouvez rayer les deux cinq en laissant votre réponse simplifiée, 3/7.

$Image intitulée Simplifier les fractions algébriques, étape 3$

3. Supprimer les facteurs des expressions algébriques tout comme les nombres normaux. Dans l`exemple précédent, vous pouvez facilement supprimer le 5 de 15, et le même principe s`applique à des expressions plus complexes telles que 15x - 5. Trouver un facteur que les deux nombres ont en commun. Ici, la réponse est 5, car vous pouvez diviser à la fois 15x et -5 par le nombre cinq. Comme précédemment, vous supprimez le facteur commun et le multipliez par ce qui reste.`
15x - 5 = 5 *(3x - 1) Pour vérifier votre travail, multipliez simplement les cinq dans la nouvelle expression - vous vous retrouverez avec les mêmes nombres que ceux avec lesquels vous avez commencé.

$Image intitulée Simplifier les fractions algébriques Étape 4$

4. Vous pouvez désormais supprimer des termes complexes comme des termes simples. Le même principe que pour les fractions régulières fonctionne également pour les fractions mathématiques. C`est le moyen le plus simple de simplifier les fractions. Prenez la fraction :
(x+2)(x-3)
(x+2)(x+10)
Remarquez comment le terme (x+2) apparaît à la fois au numérateur (en haut) et au dénominateur (en bas). En tant que tel, vous pouvez les supprimer pour simplifier la fraction algébrique, tout comme vous avez supprimé le 5 de 15/35 :
~~(x+2)~~(x-3)→(x-3)
~~(x+2)~~(x+10)→(x+10) Cela donne la réponse finale : (x-3)/(x+10).

Méthode 2 sur 3: Simplifier les fractions

$Image intitulée Simplifier les fractions algébriques, étape 5$

1. Trouver un facteur commun au numérateur (la partie supérieure de la fraction). La première chose à faire lors de la simplification d`une fraction algébrique est de simplifier chaque partie de la fraction. Commencez par la partie supérieure et rayez autant de chiffres que possible. À titre d`exemple, nous utiliserons cet exercice :
9x-3
15x+6
Commencer par le compteur : 9x – 3. Il y a un facteur commun pour 9x et -3, qui est 3. Travaillez les 3 crochets extérieurs comme vous le feriez avec n`importe quel autre nombre, en laissant 3*(3x-1). Voici votre nouveau compteur :
3 (3x-1)
15x+6

$Image intitulée Simplifier les fractions algébriques Étape 6$

2. Trouver un facteur commun au dénominateur.En continuant l`exemple ci-dessus, isolez le dénominateur, 15x+6. Recherchez à nouveau un numéro qui correspond aux deux parties. Ici aussi, vous pouvez omettre un facteur de trois, de sorte qu`il vous reste 3 * (5x +2). Incorporez votre nouveau dénominateur dans l`équation :
3 (3x-1)
3(5x+2)

$Image intitulée Simplifier les fractions algébriques Étape 7$

3. Supprimer les termes similaires. C`est l`étape où vous pouvez vraiment simplifier la fraction. Prenez tous les termes qui sont à la fois au numérateur et au dénominateur et supprimez-les. Dans ce cas, nous pouvons rayer le 3 du haut et du bas.
3(3x-1)→(3x-1)
3(5x+2)→(5x+2)

$Image intitulée Simplifier les fractions algébriques Étape 8$

4. Savoir quand l`équation est complètement simplifiée. Une fraction est simplifiée lorsqu`il n`y a plus de facteurs communs en haut ou en bas. N`oubliez pas que vous ne pouvez pas supprimer les facteurs à l`intérieur des parenthèses - dans l`exemple de problème, vous ne pouvez pas factoriser le x de 3x et 5x, car les termes complets sont en fait (3x -1) et (5x + 2). L`exemple est donc complètement simplifié, avec si la réponse finale :
(3x-1)
(5x+2)

$Image intitulée Simplifier les fractions algébriques Étape 9$

5. Essayez un exercice pratique. La meilleure façon d`apprendre est de continuer à essayer de simplifier les fractions mathématiques. Les réponses sont en dessous des problèmes.
4(x+2)(x-13)
(4x+8)Réponse: (x=13)
2x-x
5xRéponse:(2x-1)/5

Méthode 3 sur 3: Astuces pour résoudre des problèmes plus délicats

$Image intitulée Simplifier les fractions algébriques Étape 10$

1. « Inverser » les fractions pour les factoriser par des nombres négatifs. Disons que nous avons l`équation suivante :
3(x-4)
5(4-x)
Notez comment (x-4) et (4-x) presque sont identiques, mais vous ne pouvez pas les rayer car ils sont inversés. Cependant, (x - 4) peut être écrit comme -1 *(4 - x) de la même manière que vous réécrivez (4 + 2x) comme 2 *(2 + x). C`est ce qu`on appelle "sortir de la parenthèse".
-1 *3 (4-x)
5(4-x)
Maintenant, nous pouvons simplement omettre les deux identiques (4-x):
-1 *3~~(4-x)~~
5~~(4-x)~~
De là découle la réponse finale : -3/5

$Image intitulée Simplifier les fractions algébriques Étape 11$

2. Reconnaître la différence de deux carrés en travaillant. La différence de deux carrés consiste simplement à soustraire un nombre au carré d`un autre, comme l`expression (a - b). La différence des carrés parfaits est toujours simplifiée en deux parties, en ajoutant et en soustrayant les racines carrées. Dans tous les cas, vous pouvez simplifier la différence des carrés parfaits comme ceci :
a - b = (a+b)(a-b) Cela peut être très utile lorsque vous essayez de trouver des termes similaires dans des fractions mathématiques.

Exemple : x - 25 = (x+5)(x-5)

$Simplifier les fractions mathématiques$

3. simplifier les polynômes. Les polynômes ou polynômes sont des expressions algébriques complexes avec plus de deux termes, telles que : x + 4x + 3. Heureusement, de nombreux polynômes peuvent être simplifiés par « factorisation ». L`expression précédente, par exemple, peut être réécrite comme (x+3)(x+1).

$Simplifier les fractions mathématiques$

4. Rappelez-vous que les variables peuvent également être factorisées. Ceci est particulièrement utile pour les expressions avec des exposants, telles que x + x. Vous pouvez omettre le plus grand exposant comme facteur. Dans ce cas : x + x = x(x + 1).

Des astuces

Vérifiez votre travail sur la factorisation en multipliant le facteur dans l`équation - vous obtiendrez le même nombre avec lequel vous avez commencé.
Éliminez toujours les plus grands nombres possibles pour simplifier complètement votre équation.