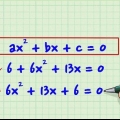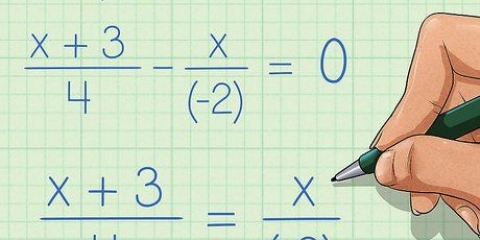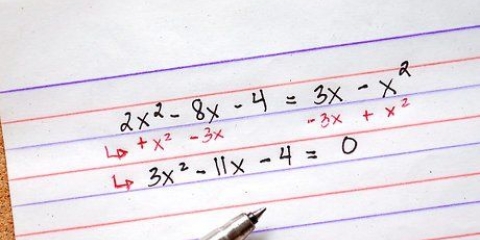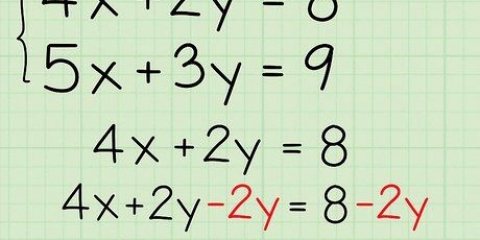Par exemple : si vous voulez diviser 20 en facteurs, vous pouvez écrire que 4×5. Notez que les termes variables peuvent également être écrits comme des facteurs. - Par exemple, 20x peut être écrit comme 4(5x). Les nombres premiers ne peuvent pas être écrits comme des facteurs car ils ne sont divisibles que par eux-mêmes et 1. 
heinchauves-souris mlever huit Wtic Vmultiplier réelen ôcompter unesoustraire 

Par exemple, trouvons les termes similaires dans notre équation 1 + 2x - 3 + 4x. 2x et 4x ont tous deux la même variable élevée à la même puissance (dans ce cas, les variables x n`ont aucun exposant). De plus, 1 et -3 sont des termes égaux, car aucun n`a de variable. Donc dans cette équation sont 2x et 4x et 1 et-3 termes égaux. 
Nous ajoutons les termes égaux dans notre exemple ensemble. 2x + 4x = 6x 1 + -3 = -2 
Dans notre exemple, les termes simplifiés étaient 6x et -2, donc la nouvelle expression devient 6x - 2. Cette expression simplifiée est équivalente à l`originale (1 + 2x - 3 + 4x), mais est plus courte et plus facile à calculer avec. Il est plus facile de factoriser, ce qui, comme nous le verrons ci-dessous, est une compétence importante pour pouvoir simplifier. 
Par exemple, supposons que nous ayons l`équation 5(3x-1) + x((2x)/(2)) + 8 - 3x. Il serait alors incorrect de considérer immédiatement 3x et 2x comme des termes égaux et de les combiner, car les parenthèses dans l`expression dictent que nous devons d`abord effectuer d`autres opérations. Tout d`abord, effectuons les opérations arithmétiques dans l`expression selon l`ordre des opérations, pour obtenir les termes que nous avons bien peut utiliser. Voir ci-dessous: 5(3x-1) + x((2x)/(2)) + 8 - 3x 15x - 5 + x(x) + 8 - 3x 15x - 5 + x + 8 - 3x. passe à présent puisque les seules opérations restantes sont l`addition et la soustraction, pouvons-nous combiner les termes similaires. x + (15x - 3x) + (8 - 5) x + 12x + 3 

Factorisons notre équation en utilisant le plus grand diviseur commun, 3. Pour ce faire, nous divisons chaque terme par 3. 9x/3 = 3x 27x/3 = 9x -3/3 = -1 La nouvelle expression est donc 3x + 9x - 1. 
Pour notre exemple d`expression, 3x + 9x - 1, nous mettons l`expression entre parenthèses et multiplions ce terme par le plus grand diviseur commun de l`équation d`origine à convertir 3 (3x + 9x - 1) pour obtenir. Cette équation est équivalente à l`originale, 9x + 27x - 3. 
Supposons que notre exemple d`expression d`origine, 9x + 27x - 3, soit égal au numérateur d`une fraction plus grande avec 3 comme dénominateur. Cette fraction ressemble à ceci : (9x + 27x - 3)/3. Nous pouvons utiliser la factorisation pour simplifier cette fraction. Ajoutez la forme factorisée de notre expression originale au numérateur : (3(3x + 9x - 1))/3 Notez que le numérateur et le dénominateur ont 3 comme coefficient. Si vous divisez le numérateur et le dénominateur par 3, vous obtenez : (3x + 9x - 1)/1. Parce qu`une fraction avec "1" au dénominateur est égal aux termes du numérateur, nous pouvons dire que notre fraction d`origine peut être simplifiée en 3x + 9x - 1. 

Prenons un exemple simple - √(90). Si nous prenons le nombre 90 comme produit des deux facteurs, 9 et 10, nous pouvons calculer la racine carrée de 9 pour obtenir 3, et le mettre devant le radical. En d`autres termes: (90) (9×10) (√(9) × (10)) 3 × (10) 3√(10) 
Par exemple, supposons que nous ayons l`expression 6x × 8x + (x/x). Dans tous les cas où il est nécessaire de multiplier ou de diviser des exposants, on soustrait ou on additionne respectivement les exposants, pour résoudre rapidement un terme simplifié. Voir ci-dessous: 6x × 8x + (x/x) (6×8)x + (x) 48x + x Pour une explication, voir ci-dessous : Multiplier des termes exponentiels revient essentiellement à multiplier de longues séries de termes sans exposants. Par exemple, parce que x = x × x × x et x= x × x × x × x × x, x × x = (x × x × x) × (x × x × x × x × x) ou x. De même, diviser des termes exponentiels revient à diviser de longues séquences de termes sans exposant. x/x = (x × x × x × x × x)/(x × x × x). Étant donné que tout terme du numérateur peut être annulé par rapport au même terme du dénominateur, il nous reste deux fois un x au numérateur et aucun au dénominateur, ce qui nous laisse x comme réponse.
Simplifier les équations mathématiques
Teneur
Être capable de simplifier les équations algébriques est une partie essentielle de la maîtrise des bases de l`algèbre et un outil extrêmement précieux pour tous les mathématiciens. La simplification permet à un mathématicien de changer une expression complexe, longue et/ou maladroite en une forme plus simple ou plus pratique mais équivalente. Les bases de la simplification sont assez faciles à apprendre - même pour quelqu`un qui déteste les mathématiques. En suivant quelques étapes simples, il est possible de simplifier bon nombre des expressions algébriques les plus courantes sans aucune connaissance mathématique particulière.
Pas
Méthode 1 sur 4: Comprendre les concepts clés

1. Déterminer "termes égaux" selon leurs variables et puissances. Posséder en algèbre "termes égaux" sur les mêmes variables, élevées à la même puissance. En d`autres termes, deux termes sont "similaire", lorsqu`elles ont la(les) même(s) variable(s), ou aucune, et lorsque chaque variable a la même puissance, ou aucune. L`ordre des variables dans un terme n`a pas d`importance.
- Par exemple, 3x et 4x sont des termes égaux car chaque terme a une variable x élevée à la puissance seconde. La variable x et x ne sont pas des termes égaux, car x a une puissance différente dans chaque terme. De même, -3yx et 5xz ne sont pas des termes égaux, car chaque terme est composé de différentes variables.

2. Factoriser en écrivant les nombres comme le produit de deux facteurs. La factorisation est une façon d`écrire un nombre donné comme le produit de deux facteurs. Les nombres peuvent être constitués de plusieurs facteurs - par exemple, le nombre 12, qui peut être formé par 1 × 12, 2 × 6 et 3 × 4, de sorte que nous pouvons dire que 1, 2, 3, 4, 6, et 12 sont tous des facteurs de 12. Une autre façon de voir les choses est que les facteurs d`un nombre sont les nombres par lesquels il est divisible.

3. Utilisez le mnémonique « Comment devrions-nous nous débarrasser des insuffisances » (ou comme acronyme HMWVDOA) pour vous souvenir de l`ordre des opérations. Parfois, simplifier une expression consiste simplement à effectuer les opérations dans l`expression jusqu`à ce que rien de plus ne puisse être fait. Dans ce cas, il est important de connaître l`ordre des opérations, pour éviter les erreurs de calcul. Ce mnémonique peut vous aider à vous souvenir de l`ordre des modifications - les lettres correspondent au type de modifications que vous devez effectuer et dans quel ordre. S`il y a des multiplications et des divisions dans le même problème, vous devrez effectuer ces opérations de gauche à droite lorsque vous arriverez à ce point. Idem pour l`addition et la soustraction. L`image ci-dessus donne une réponse qui n`est pas correcte. La dernière étape n`a pas fonctionné d`addition et de soustraction de gauche à droite. Il a d`abord été ajouté. Il devrait y avoir 25 - 20 = 5 puis 5 + 6 = 11.
Méthode 2 sur 4: Combiner des termes similaires

1. Écris tes équations. Les équations mathématiques les plus simples (celles avec seulement quelques variables et coefficients sous forme d`entiers, sans fractions, racines carrées, etc.) peut souvent être résolu en quelques étapes. Comme pour la plupart des problèmes mathématiques, la première étape pour simplifier une équation est d`écrire l`équation!
- Pour les étapes suivantes, nous prenons l`expression 1 + 2x - 3 + 4x par exemple.

2. Déterminer quels sont les termes similaires. Cherchez maintenant les termes similaires dans votre équation. N`oubliez pas que les termes similaires ont tous les deux la même variable et le même exposant.

3. Combiner des termes similaires. Maintenant que vous avez déterminé les termes similaires, vous pouvez commencer à les combiner pour simplifier votre équation. Additionnez des termes (ou soustrayez-les dans le cas de termes négatifs) pour simplifier chaque ensemble de termes (avec les mêmes variables et exposants) en un seul terme.

4. Faites une expression simplifiée de vos termes simplifiés. Après avoir combiné vos termes similaires, construisez une expression à partir de votre nouvel ensemble de termes plus petit. Vous devriez maintenant avoir une expression plus simple avec un terme pour chaque ensemble de variables et d`exposants dans l`expression d`origine. Cette nouvelle expression est équivalente à la première.

5. Respecter l`ordre des opérations lors de la combinaison de termes similaires. Dans des expressions très simples comme celles que nous avons traitées dans les exercices ci-dessus, il est facile de reconnaître les termes similaires. Dans les expressions plus complexes, telles que celles avec des termes entre parenthèses, des fractions et des racines, la combinaison de termes similaires ne sera pas immédiatement évidente. Dans ces cas, suivez la séquence d`opérations et effectuez les opérations sur les termes de votre expression jusqu`à ce qu`il ne vous reste plus que des additions et des soustractions.
Méthode 3 sur 4: Affacturage

1. Trouver le plus grand diviseur commun dans l`expression. La factorisation est un moyen de simplifier les expressions en supprimant les facteurs qui apparaissent dans tous les termes de l`expression. Pour commencer, trouvez le plus grand diviseur commun de tous les termes de l`expression - en d`autres termes, le plus grand nombre par lequel tous les termes de l`expression sont divisibles par.
- Supposons que nous prenons l`équation 9x + 27x - 3. Notez que chaque terme de cette équation est divisible par 3. Parce que non des termes est entièrement divisible par un autre nombre plus grand, on peut dire que 3 est le plus grand dénominateur commun de notre expression.

2. Diviser les termes de l`expression par le plus grand diviseur commun. Divisez ensuite chaque terme de votre équation par le plus grand diviseur commun que vous venez de trouver. Les termes résultants auront tous des coefficients plus petits que ceux de l`expression originale.

3. Écrivez votre expression comme le produit du plus grand diviseur commun et des termes restants. Votre nouvelle expression n`est pas la même que l`ancienne, il n`est donc pas correct de dire qu`il s`agit de la version simplifiée. Pour rendre la nouvelle expression égale à l`ancienne, nous devrons tenir compte du fait qu`elle est divisée par le plus grand diviseur commun. Mettez votre nouvelle expression entre parenthèses et écrivez le plus grand diviseur commun de l`équation d`origine comme coefficient de l`expression également entre parenthèses.

4. Facteur pour simplifier les fractions. Vous vous demandez peut-être maintenant pourquoi la factorisation est utile si la nouvelle expression doit être multipliée à nouveau après avoir supprimé le plus grand diviseur commun. La factorisation permet à un mathématicien d`utiliser un certain nombre d`astuces pour simplifier une expression. L`une des astuces les plus simples utilise le fait que multiplier le numérateur et le dénominateur d`une fraction par le même nombre produit une fraction dans les mêmes proportions. Voir ci-dessous:
Méthode 4 sur 4: Appliquer simplifier

1. Simplifier les fractions en divisant par des facteurs égaux. Comme mentionné ci-dessus, si le numérateur et le dénominateur d`une expression ont les mêmes facteurs, ces facteurs peuvent être retirés de la fraction. Parfois, cela nécessite que le numérateur, le dénominateur ou les deux soient pris en compte (comme ce fut le cas dans l`exemple ci-dessus), tandis que dans d`autres cas, les facteurs communs sont immédiatement apparents. Notez qu`il est également possible de diviser les termes individuels au numérateur par l`expression au dénominateur, pour obtenir une expression simplifiée.
- Attaquons un exemple qui ne vous oblige pas forcément à les écrire pour simplifier. Supposons que vous ayez la fraction (5x + 10x + 20)/10, vous pouvez diviser chaque terme du numérateur par le 10 du dénominateur, pour simplifier le tout, même si le "5" en 5x pas supérieur à 10 et il n`est pas possible de choisir 10 comme facteur.
- En faisant cela, nous obtenons ((5x)/10) + x + 2. Si nous voulons, nous pouvons réécrire le premier terme sous la forme (1/2)x pour obtenir (1/2)x + x + 2.

2. Utiliser des racines carrées pour simplifier les racines. Les expressions sous le signe d`une racine carrée sont appelées équations de racine carrée. Vous pouvez simplifier cela en déterminant les racines carrées (facteurs qui forment eux-mêmes une seconde puissance d`un entier), après quoi vous soustrayez la racine carrée de ces facteurs pour les supprimer du signe radical.

3. Additionnez les exposants lorsque vous multipliez deux termes exponentiels et soustrayez-les lorsque vous divisez. Certaines équations algébriques nécessitent de multiplier ou de diviser des termes exponentiels. Vous ne calculez pas chaque terme exponentiel et vous ne multipliez ou ne divisez pas manuellement, mais compter vous additionnez les exposants de chaque terme lorsque vous les multipliez ensemble et les tirez-vous lorsque vous les partagez, vous gagnez beaucoup de temps. Vous pouvez également appliquer ce concept pour simplifier les équations à plusieurs variables.
Des astuces
- N`oubliez pas que vous devez considérer ces chiffres comme positifs ou négatifs. Beaucoup de gens sont coincés avec ça et pensent, "Quel signe dois-je mettre ici?"
- Demandez de l`aide si vous en avez besoin!
- Simplifier des équations mathématiques n`est pas facile, mais une fois que vous avez compris, vous pouvez l`utiliser pour le reste de votre vie.
Mises en garde
- Veillez à ne pas ajouter accidentellement des nombres, des exposants ou des opérations supplémentaires qui n`y appartiennent pas.
- Faites toujours attention aux termes égaux et ne vous laissez pas tromper par les exposants.
Articles sur le sujet "Simplifier les équations mathématiques"
Оцените, пожалуйста статью
Populaire