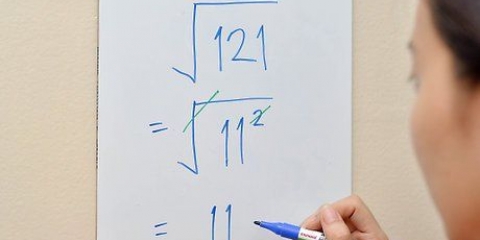Exemple : l`expression suivante 2x + 4(5 + 2) + 3 - (3 + 4/2). Résolvez d`abord les termes entre parenthèses, donc 5 + 2 et 3 + 4/2. 5 + 2 = sept. 3 + 4/2 = 3 + 2 = 5. Le terme entre la deuxième paire de parenthèses devient 5 car nous devons d`abord calculer 4/2 et ensuite seulement faire l`addition. Si nous travaillions simplement de gauche à droite, alors la somme serait 3 + 4 : 2, où d`abord 3 + 4 puis 7/2 seraient calculés, ce qui donnerait une mauvaise réponse 7/2. Remarque - si plusieurs parenthèses sont imbriquées (parenthèses entre parenthèses), dissolvez d`abord celle intérieure et travaillez vers les parenthèses extérieures. 
Après avoir résolu les parenthèses, l`exemple ressemblait à ceci. 2x + 4(7) + 3 - 5. La seule puissance dans notre exemple est 3, et elle est égale à 9. L`expression devient maintenant 2x + 4(7) + 9 - 5. 
Il y a deux multiplications dans le problème : 2x (2x est 2 × x) et 4(7). Nous ne connaissons pas la valeur de x, alors laissons-le comme 2x. 4(7) = 4 × 7 = 28. Nous pouvons écrire cela différemment comme 2x + 28 + 9 - 5. 
Puisque nous avons déjà résolu un problème de division qui était entre parenthèses, il n`y a plus de problèmes de division dans notre problème, nous pouvons donc sauter cette étape. Cela soulève un point important - si une opération ne se produit pas dans une expression, passez à l`opération suivante comme indiqué dans les règles des règles mathématiques. 
Notre expression est maintenant partiellement simplifiée en "2x + 28 + 9 - 5". Maintenant, nous additionnons autant que possible - de gauche à droite. Nous ne pouvons pas ajouter 2x aux autres nombres, car nous ne connaissons pas la valeur de x, nous sautons donc celui-ci. 28 + 9 = 37, nous pouvons donc réécrire l`expression sous la forme "2x + 37 - 5". 
Dans notre expression, "2x + 37 - 5", il n`y a qu`une seule soustraction,37 - 5 = 32 
Notre réponse finale est "2x + 32". Nous ne pouvons pas résoudre l`addition sans connaître la valeur de x, mais une fois que nous le faisons, c`est beaucoup plus facile à résoudre que l`expression d`origine. 

Par exemple, supposons que nous devions résoudre la fraction 36/60. Si nous avons une calculatrice à portée de main, la réponse (6) est calculée comme ceci. Si nous n`avons pas cela, nous pouvons aller loin en éliminant des facteurs similaires. Une autre façon de penser à 36/60 est comme (6 × 6)/(6 × 10). Cela peut à nouveau être réécrit comme 6/6 × 6/10. 6/6 = 1, donc notre expression devient 1 × 6/10 = 6/10. Mais nous n`en sommes pas encore là - les deux 6 et 10 ont le même facteur de 2. En répétant la procédure ci-dessus, on garde3/5 au sujet de. 
Supposons que nous ayons l`expression (3x + 3x)/(-3x + 15x).Cette fraction peut être réécrite sous la forme (x + 1)(3x)/(3x)(5 - x), 3x apparaît à la fois au numérateur et au dénominateur. La suppression de ces facteurs de l`équation donne (x + 1)/(5 - x). De même, c`est le cas de l`équation (2x + 4x + 6)/2. Puisque chaque terme est divisible par 2, nous pouvons le réécrire sous la forme (2(x + 2x + 3))/2 et ainsi simplifier à x + 2x + 3. Attention, vous ne pouvez pas éliminer tous les termes - seulement les facteurs qui sont à la fois dans le numérateur et le dénominateur. Par exemple, l`expression (x(x + 2))/x, où le "X" peut être retiré de la fraction, laissant (x + 2)/1 = (x + 2). Mais (x + 2)/x n`est pas simplifier à 2/1 = 2. 
Par exemple, l`expression 3(x + 8 peut être simplifiée en3x + 24, tandis que 3x(x + 8) peut être simplifié en 3x + 24x. Notez que dans certains cas, comme avec des fractions variables, la constante en dehors des parenthèses peut être utilisée dans la simplification et ne doit donc pas être multipliée. Par exemple, dans la fraction (3(x + 8))/3x, le facteur 3 est à la fois au numérateur et au dénominateur, nous pouvons donc l`annuler et simplifier l`expression en (x + 8)/x. C`est plus simple et plus facile à travailler qu`avec (3x + 24x)/3x, ce qui aurait été la réponse si on avait multiplié. 
Revoyez l`expression x - 5x + 6. Cela peut être résolu en (x - 3)(x - 2). Donc, si x - 5x + 6 est le numérateur d`une équation avec l`un de ces facteurs au dénominateur (comme dans (x - 5x + 6)/(2(x - 2))), alors nous pouvons le factoriser en facteurs tels que que nous pouvons nous débarrasser du dénominateur. En d`autres termes, à (x - 3)(x - 2)/(2(x - 2)), (x - 2) tombe, nous laissant(x - 3)/2 laissé pour compte. Comme indiqué ci-dessus, vous pouvez également résoudre une équation avec factorisation, surtout si elle est mise égale à zéro. Par exemple : prenons l`équation x - 5x + 6 = 0. La factorisation nous donne (x - 3)(x - 2) = 0. Puisqu`un nombre fois zéro est égal à zéro, nous pouvons définir les deux termes égaux à zéro, pour trouver la réponse à ce problème. Donc la réponse à l`équation est x=3 et x= 2.
Simplifier les expressions mathématiques
Teneur
Les problèmes mathématiques demandent souvent une réponse "le plus simple possible" écrire, c`est-à-dire donner une réponse le plus élégamment possible. Alors qu`une expression longue et maladroite et une version plus courte et plus élégante signifient techniquement la même chose, une réponse n`est souvent pas acceptée tant qu`elle n`a pas été simplifiée autant que possible.De plus, les réponses simplifiées sont également plus faciles à utiliser. `C`est pourquoi apprendre à simplifier est une compétence essentielle pour les futurs mathématiciens.
Pas
Méthode 1 sur 2: L`ordre des opérations mathématiques

1. L`ordre des opérations. Lors de la simplification des expressions mathématiques, vous ne pouvez pas simplement évaluer de gauche à droite. Certaines opérations priment sur d`autres et doivent donc être effectuées en premier. Si vous ne le faites pas, vous risquez d`avoir une mauvaise réponse. L`ordre des opérations en mathématiques est le suivant : parenthèses, exponentiation et enracinement, multiplication et division, addition et soustraction. Un mnémonique pour se souvenir de cette séquence est "Comment devrions-nous nous débarrasser de l`inadéquation " ou "HMWVDOA".
- Notez que même si une connaissance de base des opérations est suffisante pour résoudre la plupart des expressions standard, des techniques spéciales sont nécessaires pour résoudre les expressions contenant des variables, y compris la plupart des polynômes. Regardez la deuxième méthode pour plus d`informations.

2. Commencez par résoudre tous les termes entre parenthèses. En mathématiques, les parenthèses signifient que tous les termes qu`elles contiennent doivent être résolus séparément de l`expression environnante. Quelles que soient les opérations, assurez-vous d`abord de résoudre tous les termes entre parenthèses si vous souhaitez simplifier une expression. Gardez à l`esprit que les règles de calcul de l`ordre des opérations s`appliquent également entre parenthèses. Alors là aussi d`abord les parenthèses, puis l`exponentiation, etx.

3. Maintenant dissoudre les pouvoirs. Après avoir travaillé les parenthèses, vous pouvez maintenant passer à l`exponentiation. Résolvez-les un par un.

4. Résolvez maintenant les sommes de multiplication. Rappelez-vous qu`une multiplication peut être écrite de plusieurs manières. Avec un point, sans point ou avec un symbole ×. Mais aussi quelque chose comme 4(x)) indique une multiplication.

5. Continuer avec les problèmes de division. Si vous recherchez des problèmes de division, rappelez-vous que ceux-ci peuvent également être écrits de différentes manières. Le simple symbole , avec deux points ou une barre oblique (comme 3/4) indiquent tous une division.

6. Additionner. Additionnez maintenant les différents termes. Calculez cela de gauche à droite, tel qu`il est dans l`expression et selon ce qui est le plus pratique. Par exemple, dans la somme 49 + 29 + 51 +71, il est plus facile de diviser le problème en blocs suivants : 49 + 51 = 100, 29 + 71 = 100 et 100 + 100 = 200. C`est plus facile que 49 + 29 = 78, 78 + 51 = 129 et 129 + 71 = 200.

sept. soustraire. La dernière étape des opérations consiste à soustraire les termes restants. Travaillez le reste de votre expression, de gauche à droite. Vous pouvez ajouter des nombres négatifs dans cette étape ou dans l`étape précédente - cela n`a pas d`importance pour votre réponse.

8. Voir votre expression. Après avoir parcouru la séquence des opérations, vous vous retrouvez avec un certain nombre de termes sous la forme la plus simplifiée. S`il y a une ou plusieurs variables dans l`expression, elles restent en grande partie inchangées. Simplifier les expressions avec des variables nécessite que nous résolvions davantage ces équations pour les inconnues, ou en utilisant des méthodes spéciales (voir l`étape suivante).
Méthode 2 sur 2: Simplifier des expressions complexes

1. Additionner des puissances variables égales ensemble. Lorsqu`il s`agit d`expressions contenant des variables, il est important de se rappeler que les termes ayant la même variable et le même exposant (ou "termes égaux") peuvent être additionnés (ou soustraits) comme des nombres normaux. Les termes devoir ont non seulement la même variable, mais aussi le même exposant. Par exemple, 7x et 5x peuvent être additionnés, mais 7x et 5x ne peuvent pas.
- Cette règle peut également être étendue aux termes multivariés. Par exemple, 2xy peut être ajouté à -3xy, mais pas à -3xy ou -3y.
- Prenons les expressions suivantes :x + 3x + 6 - 8x. Dans cette expression, nous pouvons additionner les termes 3x et -8x ensemble car ils sont égaux l`un à l`autre. Notre expression se simplifie alors : x - 5x + 6.

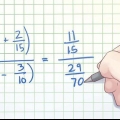
2. Simplifier les fractions en éliminant ou en divisant les facteurs. Les fractions constituées uniquement de nombres (et d`aucune variable) peuvent être simplifiées de plusieurs manières. Une fraction n`est qu`une somme de division et doit être traitée comme telle. De plus, si la même multiplication se produit au numérateur ou au dénominateur, elle peut être éliminée, car ils donnent déjà la réponse 1 lorsqu`ils sont partagés. En d`autres termes, si le numérateur et le dénominateur ont tous deux le même facteur, alors il peut être retiré de la fraction, simplifiant le résultat.

3. Si vous avez affaire à des fractions contenant des variables, essayez d`éliminer les variables. Ces expressions offrent des possibilités uniques pour simplifier. Comme les fractions régulières, les fractions variables vous permettent de supprimer les facteurs qui sont à la fois au numérateur et au dénominateur. Mais dans ce dernier cas, ces facteurs peuvent être aussi bien des nombres que des variables.

4. Multiplier les termes entre parenthèses par leurs constantes. Lorsqu`il s`agit de termes variables entre parenthèses plus une constante, multiplier n`importe quel terme à l`intérieur des parenthèses par la constante à l`extérieur des parenthèses peut donner une expression plus simple.Cela s`applique à la fois aux constantes numériques et aux constantes avec des variables.

5. Simplifiez-vous en factorisant. C`est une technique qui peut simplifier certaines équations. Lors de l`affacturage, pensez à quelque chose qui est à l`opposé de "multiplier les parenthèses" – parfois une équation peut être représentée plus simplement comme deux termes multipliés ensemble que comme une seule équation. Cela est particulièrement vrai si vous pouvez éliminer une partie de l`équation avec. Dans certains cas (comme avec les équations quadratiques), vous pouvez également résoudre l`équation elle-même avec la factorisation.
Articles sur le sujet "Simplifier les expressions mathématiques"
Оцените, пожалуйста статью
Similaire
Populaire