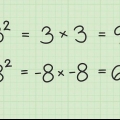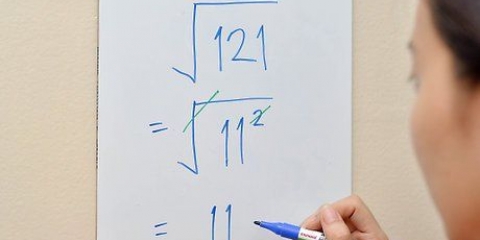Simplifier les racines carrées

Teneur

Pas
Des astuces
Mises en garde

Simplifier une racine carrée n`est pas aussi difficile qu`il y paraît. Pour simplifier une racine carrée, il vous suffit de factoriser le nombre de la racine carrée et d`essayer de prendre la racine carrée d`un ou des deux facteurs. Une fois que vous connaissez certains nombres carrés communs et savez comment diviser un nombre en facteurs, vous êtes sur la bonne voie pour simplifier une racine carrée. Voici comment vous pouvez apprendre cela rapidement.

Pas

Méthode 1 sur 4: Simplifier la racine carrée d`un nombre

Image intitulée Simplifier une racine carrée Étape 1

1. Apprendre quelques nombres carrés et leurs racines. Mettre au carré, multiplier un nombre par lui-même, fait un nombre au carré (parfaitement carré). Par exemple : 25 est un nombre au carré car 5 x 5 ou 5 est égal à 25. Connaître au moins les 10 premiers nombres au carré peut aider à reconnaître et à simplifier les racines carrées. Voici les dix premiers nombres au carré :

1 = 1
2 = 4
3 = 9
4 = 16
5 = 25
6 = 36
7 = 49
8 = 64
9 = 81
10 = 100

2. Trouver la racine carrée d`un nombre carré. Si vous voyez un nombre carré sous un radical, il vous suffit de supprimer le radical (√ ) et d`écrire la racine carrée du nombre carré. Si vous aviez déjà appris cela par cœur, alors vous avez terminé. Si le nombre est trop grand et que vous n`êtes pas sûr qu`il s`agisse d`un nombre carré, essayez de trouver la racine carrée avec votre calculatrice pour vérifier s`il produit un bon nombre rond. Par exemple : à √25 vous savez que la réponse est égale à 5 car 25 est un nombre au carré.

Méthode 2 sur 4: Simplifier une racine carrée en factorisant

Image intitulée Simplifier une racine carrée Étape 4

1. Si le nombre est pair, divisez-le par 2. Trouver les facteurs d`un nombre consiste à trouver tous les nombres qui, multipliés ensemble, produisent ce nombre, ce qui facilite la détermination de sa racine carrée. S`il s`agit d`un nombre pair, la première chose que vous pouvez faire est de diviser le nombre par 2. Dans cet exemple, vous pouvez diviser √98 en √(2x49), car 98 : 2 =49. Si le nombre n`est pas divisible par 2, essayez 3, 4, 5, et ainsi de suite, jusqu`à ce que vous trouviez la bonne combinaison.

Image intitulée Simplifier une racine carrée Étape 5

2. Divisez ces facteurs en facteurs pour trouver d`autres nombres carrés. Voyez si vous pouvez continuer à diviser le nombre en facteurs. 2 est premier et n`a que lui-même et 1 comme diviseur. Mais 49, l`autre facteur, peut encore être divisé en 7 x 7, car c`est un nombre carré. Vous pouvez donc réécrire la racine √(2x49) sous la forme √(2x7x7), ou √[2(7)], ce qui signifie que nous avons déjà trouvé le nombre carré que nous cherchions.

Image intitulée Simplifier une racine carrée Étape 6

3. Simplifier la racine carrée. Puisque √98= √[2(7)], il est possible de placer un 7 en dehors du radical et de simplifier la réponse à 7√2. Donc √49 ou aussi (7 x 7), puis devient 7 dès qu`on le place en dehors du radical. Si vous replacez le 7, il redevient un nombre carré et donc 49. Donc, 98 = 7√2.

Méthode 3 sur 4: Autres méthodes pour simplifier une racine carrée

1. Si vous ne parvenez pas immédiatement à trouver un nombre carré, divisez le nombre plus loin. Par exemple, si le problème est √48, vous continuez à diviser jusqu`à ce que vous ne puissiez pas dépasser 2x2, de sorte que 4 devienne un coefficient du radical et 3 reste à l`intérieur du radical. Voici comment cela fonctionne :

48 = (2 x 24)
(2x24) = (2x12x2)
(2x12x2) = (2x6x2x2)
(2x6x2x2) = (2x3x2x2x2)
(2x3x2x2x2) = (2x3)
(2 x 3)= 4√3
48 = 4√3

2. Rappelez-vous que vous ne pouvez pas simplifier un nombre premier. C`est parce que les facteurs ici sont 1 et le nombre premier lui-même. Par exemple : √17 ne peut pas être simplifié car 17 est premier.

3. Division en facteurs de plus d`un nombre au carré. Si les facteurs du nombre contiennent plus d`un nombre carré, prenez-les tous en dehors du radical. Si vous avez trouvé plusieurs carrés en simplifiant, prenez-les tous en dehors du radical et multipliez-les. Par exemple : supposons que vous vouliez simplifier le nombre √32, puis le diviser en facteurs 4 x 4 x 2, en notant que le nombre carré 4 apparaît deux fois. Faites ce 16√2 qui finira par rapporter 4√2.

4. Ne pas confondre le coefficient avec une racine de puissance plus élevée. 3√125, par exemple, est égal à 3 x √125, mais √125 est la racine cubique de 125. (car 5 x 5 x 5 = 125, 125 = 5.)

Méthode 4 sur 4: Connaître la terminologie

1. Rappelez-vous que le radical (√) est le symbole de la racine carrée. Par exemple, dans le problème √25, "??" le signe radical.

2. Rappelez-vous que le radical est le nombre sous le radical. Trouver la racine carrée de ce nombre. Par exemple : à √25 est "25" le nombre racine.

3. Rappelez-vous que le coefficient est le nombre en dehors du radical. Ce nombre multiplie la racine carrée ; Cela peut être trouvé à gauche du signe radical, le symbole √. Par exemple : à 7√2, "sept" le coefficient.

4. Rappelez-vous qu`un facteur est un nombre qui entre complètement dans un autre nombre. Par exemple : 2 est un facteur 8 car 8 4 = 2, mais 3 n`est pas un facteur 8 car 8÷3 ne répond pas à un entier. Par exemple : 5 est un facteur de 25 car 5 x 5 = 25.

5. Comprendre le sens de la simplification d`une racine carrée. Simplifier une racine carrée consiste simplement à diviser un carré de racine carrée en facteurs, puis à le déplacer vers la gauche du radical, en laissant l`autre facteur à l`intérieur du radical. Si le nombre est un nombre carré alors vous pouvez supprimer le signe radical dès que vous avez écrit sa racine carrée. Par exemple : √98 peut être simplifié en 7√2.

Des astuces

Une façon de trouver des carrés pour diviser vos nombres au carré est de rechercher des carrés dans votre liste en commençant par le plus petit nombre après votre nombre au carré. Par exemple : si vous cherchez le nombre carré de 27, commencez à 25 et arrêtez-vous à 9, car vous avez trouvé le plus grand diviseur qui est un nombre carré.

Mises en garde

N`utilisez pas de calculatrices, sauf à l`étape où vous essayez de déterminer combien de fois le carré entre dans la racine carrée.
Simplifier n`est pas la même chose que mettre des valeurs dans une équation.Nulle part dans l`ensemble du processus un nombre décimal ne peut apparaître n`importe où!