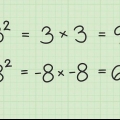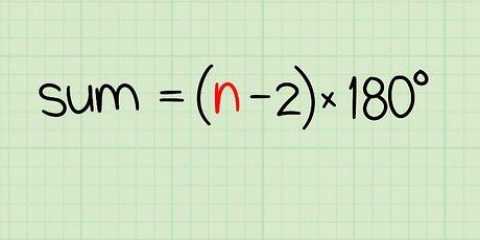Dans cet exemple, le premier ensemble de trois nombres multipliés ensemble est égal à 10. Déterminer le plus grand cube inférieur à 10. C`est 8, et sa racine cubique est 2. Écrivez le chiffre 2 au-dessus du signe radical, au-dessus du chiffre 10. Notez la valeur de  , égal à 8, en dessous du nombre 10; tracer une ligne et soustraire les nombres de la même manière que dans la division longue. Le résultat est 2.
, égal à 8, en dessous du nombre 10; tracer une ligne et soustraire les nombres de la même manière que dans la division longue. Le résultat est 2. Après cette somme négative, vous avez le premier chiffre de votre réponse. Vous devrez vérifier si ce numéro est assez exact. Dans la plupart des cas, ce ne sera pas le cas. Vous pouvez le vérifier en augmentant le nombre au cube et en voyant s`il est assez proche du résultat souhaité. Dans ce cas  est égal à 8, et ce n`est pas vraiment proche de 10, vous devez donc passer à autre chose.
est égal à 8, et ce n`est pas vraiment proche de 10, vous devez donc passer à autre chose. 
À gauche de la ligne verticale, écrivez la solution du prochain diviseur, comme la somme de trois nombres séparés. Indiquez les espaces vides pour ces numéros en soulignant trois espaces vides avec des signes plus en dessous d`eux. 


Calculez maintenant 3 fois 10 fois chacun des deux nombres qui existent dans votre solution au dessus du radical. Pour ce problème simple, cela signifie 3*10*2*1, ce qui équivaut à 60. Ajoutez ceci aux 1200 que vous aviez déjà et vous obtenez 1260. Enfin, ajoutez le carré du dernier chiffre. Dans cet exemple, c`est 1 ; et 1^2 est toujours 1. Le diviseur total est donc 1200+60+1, soit 1261. Notez ceci à gauche de la ligne verticale. 

Vous pouvez vérifier la précision de ce résultat à l`aide du cube : 2.1*2.1*2.1. Le résultat est 9 261. Si vous pensez que le résultat est assez précis, vous pouvez arrêter. Si vous voulez une réponse plus précise, vous devez passer par un autre tour. 
Prendre le prochain groupe de trois nombres vers le bas. Dans ce cas ce sont trois zéros, qui viennent après le reste 739 et donc 739.000 formes. Commencer le diviseur à 300 fois le carré du nombre actuellement au-dessus du radical. C`est  , et donc 132.300.
, et donc 132.300. Sélectionnez le chiffre suivant de votre solution afin de pouvoir le multiplier par 132.300 et moins du 739.000 de votre reste. Un bon choix serait 5, car 5*132.300=661.500. Écrivez le nombre 5 dans l`espace suivant au-dessus de la ligne radicale. Trouvez 3 fois le nombre précédent au-dessus de la ligne radicale, 21, fois le dernier chiffre que vous venez d`écrire, 5, fois 10. Cela donne  .
. Enfin, tu carré le dernier chiffre. C`est 
Additionnez les termes de votre diviseur et vous obtenez 132.300+3150+25=135.475. 
Multipliez le diviseur par le dernier chiffre de votre solution. 135.475*5=677.375. soustraire. 739.000-677.375=61.625. Considérez si la solution 2.15 est assez exacte. Calculez son cube et vous obtenez  .
. 


Dans l`exemple de problème, 600 (votre nombre cible) se situe à peu près à mi-chemin entre les nombres limites 512 et 729. Alors choisis ton 5 comme prochain numéro. 
Dans cet exemple, vous multipliez 

Par exemple, dans ce problème,  plus grand que la cible (600). Donc vous réduisez l`estimation à 8,4. Prenez le cube de ce nombre et comparez-le à votre cible. tu verras ça
plus grand que la cible (600). Donc vous réduisez l`estimation à 8,4. Prenez le cube de ce nombre et comparez-le à votre cible. tu verras ça  . C`est maintenant inférieur à votre objectif. Cela vous indique que la racine cubique de 600 doit être d`au moins 8,4, mais inférieure à 8,5.
. C`est maintenant inférieur à votre objectif. Cela vous indique que la racine cubique de 600 doit être d`au moins 8,4, mais inférieure à 8,5. 
Dans cet exemple de problème, votre dernière série de calculs montre que  , tandis que
, tandis que  . La cible (600) est légèrement plus proche de 592 que de 614. Estimez-vous donc le prochain nombre un peu moins qu`à mi-chemin entre 0 et 9. Un bon choix est 4, ce qui vous donnera une estimation de la racine cubique de 8,44.
. La cible (600) est légèrement plus proche de 592 que de 614. Estimez-vous donc le prochain nombre un peu moins qu`à mi-chemin entre 0 et 9. Un bon choix est 4, ce qui vous donnera une estimation de la racine cubique de 8,44. 
Pour cet exemple de problème, commencez par noter que  . C`est juste au-dessus de la cible, alors lâchez-en et testez 8.43. Cela donne
. C`est juste au-dessus de la cible, alors lâchez-en et testez 8.43. Cela donne  à la suite. Vous savez donc que la racine cubique de 600 est un peu plus de 8,43 et un peu moins de 8,44.
à la suite. Vous savez donc que la racine cubique de 600 est un peu plus de 8,43 et un peu moins de 8,44. 
Pour l`exemple de la racine cubique de 600, en supposant deux nombres décimaux, 8,43 est à moins de 1 du nombre cible. Si vous continuez jusqu`à trois chiffres après la virgule, vous verrez que  si le résultat est inférieur de 0,1 à la réponse réelle.
si le résultat est inférieur de 0,1 à la réponse réelle. 

Pour en savoir plus sur le binôme de Newton et obtenir ce résultat, en savoir plus sur la multiplication de binômes sur wikiHow. Si vous voulez une version plus détaillée et rapide, lisez plus sur le Triangle de Pascal. 

Le premier terme contient un pluriel de 1000. Vous choisissez d`abord un nombre qui pourrait être élevé au cube tout en restant dans la plage de division longue en tant que premier chiffre. Cela donne le terme 1000A^3 dans le binôme. Le deuxième terme du binôme de Newton a un coefficient de 300. (C`est de la part de  .) N`oubliez pas que lors du calcul de la racine cubique, le premier chiffre de chaque étape a été multiplié par 0300.
.) N`oubliez pas que lors du calcul de la racine cubique, le premier chiffre de chaque étape a été multiplié par 0300. Le deuxième chiffre de chaque étape du calcul de la racine cubique provient du troisième terme du binôme de Newton. Dans le binôme de Newton, vous voyez le terme 30AB^2. Le dernier chiffre de chaque étape est le terme B^3. 
Calculer les racines cubiques à la main
Teneur
À l`aide d`une calculatrice, calculer la racine cubique d`un nombre en appuyant simplement sur quelques touches. Mais peut-être que vous n`avez pas de calculatrice ou que vous voulez impressionner vos amis avec votre capacité à calculer une racine cubique à la main. Il existe une méthode qui a l`air un peu dure à première vue, mais qui fonctionne très facilement avec un peu de pratique. Il est utile d`avoir des connaissances préalables dans le domaine de l`arithmétique et du calcul des nombres cubiques.
Pas
Partie 1 sur 3: Élaboration d`un exemple de devoir

1. Préparer le devoir. Résoudre la racine cubique d`un nombre ressemblera à résoudre une division longue, avec quelques différences ici et là. La première étape consiste à écrire correctement le problème.
- Écrivez le nombre que vous voulez trouver la racine cubique de. Écrivez les nombres en groupes de trois, où la virgule est le point de départ. Dans cet exemple, vous allez trouver la racine cubique de 10. Écrivez-le comme 10 000 000. Les zéros sont nécessaires pour l`exactitude de la réponse.
- Tracer un radical du cube sur le nombre. Cela sert le même but que la longue ligne de division. La seule différence est la forme du symbole.
- Placez une virgule au-dessus de la ligne, directement au-dessus de la virgule dans le nombre d`origine.

2. Connaître les cubes des unités. Vous l`utiliserez dans vos calculs. Il s`agit des troisièmes pouvoirs suivants :











3. Trouvez le premier chiffre de votre réponse. Sélectionnez un nombre qui, au cube, donne le plus grand résultat possible qui est inférieur au premier ensemble de trois nombres.
 , égal à 8, en dessous du nombre 10; tracer une ligne et soustraire les nombres de la même manière que dans la division longue. Le résultat est 2.
, égal à 8, en dessous du nombre 10; tracer une ligne et soustraire les nombres de la même manière que dans la division longue. Le résultat est 2. est égal à 8, et ce n`est pas vraiment proche de 10, vous devez donc passer à autre chose.
est égal à 8, et ce n`est pas vraiment proche de 10, vous devez donc passer à autre chose.
4. Faire la queue pour le chiffre suivant. Écrivez le prochain groupe de trois nombres dans le reste et tracez une courte ligne verticale à gauche du nombre résultant. Ce sera le nombre que nous utiliserons pour déterminer le chiffre suivant dans votre solution de racine cubique. Dans cet exemple, ce sera 2000, qui est créé à partir du reste 2 de la somme négative précédente, avec le groupe de trois zéros que vous avez retiré.

5. Trouver le début du prochain diviseur. Pour la première partie du diviseur, écris trois cents fois le carré de tout ce qui est au-dessus du radical. Dans ce cas, c`est 2 ; 2^2 vaut 4 et 4*300=1200. Alors écris 1200 dans le premier espace vide. Le diviseur pour cette étape de la solution va être 1200, plus quelque chose d`autre que vous calculerez dans une minute.

6. Trouvez le prochain nombre dans votre racine cubique. Trouvez le chiffre suivant de votre solution en sélectionnant ce que vous pouvez multiplier par le diviseur (1200 et quelque chose), puis soustrayez du reste de 2000. Cela ne peut être que 1, car 2 fois 1200 égale 2400, ce qui est supérieur à 2000. Écrivez le nombre 1 dans l`espace suivant au-dessus du radical.

sept. Trouver le reste du diviseur. Le diviseur dans cette étape de la solution se compose de trois parties. La première partie est le 1200 que vous avez déjà. Vous devrez maintenant ajouter deux termes supplémentaires pour compléter le diviseur.

8. Multiplier et soustraire. Arrondissez cette partie de la solution en multipliant le dernier chiffre de votre solution - dans ce cas le nombre 1 - par le diviseur que vous venez de calculer (1261). 1*1261 = 1261. Ecrivez ceci en dessous de 2000 et soustrayez 1261 pour obtenir 739.

9. Décidez que vous devriez aller plus loin pour une réponse plus précise. Après avoir terminé la somme négative de chaque étape, vous devez vérifier si votre réponse est suffisamment exacte. Pour la racine cubique de 10 : après la première somme moins, la racine cubique n`était que de 2, et ce n`est pas vraiment exact. Maintenant, après le deuxième tour, la solution est 2.1.

dix. Déterminer le croupier pour le prochain tour. Dans ce cas, pour plus de pratique et une réponse plus précise, répétez les étapes pour un autre tour, comme suit :
 , et donc 132.300.
, et donc 132.300. .
.

11. Multiplier le diviseur par le résultat. Après avoir calculé le diviseur au tour suivant et étendu votre solution d`un chiffre supplémentaire, procédez comme suit :
 .
.
12. Écrivez votre réponse finale. Le résultat au-dessus du radical est la racine cubique, avec une précision de trois chiffres significatifs. Dans cet exemple, la racine cubique de 10 est égale à 2,15. Vérifiez cela en calculant 2,15^3=9,94 qui peut être arrondi à 10. Si vous avez besoin d`une réponse plus précise, continuez jusqu`à ce que vous soyez satisfait.
Partie 2 sur 3: Trouver la racine cubique par estimation répétée

1. Utilisez des nombres cubiques pour définir les limites supérieure et inférieure. Lorsqu`on vous demande une racine cubique d`un certain nombre, commencez par choisir un cube qui s`en rapproche le plus possible sans être plus grand que votre nombre cible.
- Par exemple, si vous voulez trouver la racine cubique de 600, souvenez-vous (ou utilisez une table de cubes) que
et
. Par conséquent, la solution de la racine cubique de 600 sera quelque chose entre 8 et 9. Utilisez les nombres 512 et 729 comme limites supérieure et inférieure pour votre solution.

2. Devinez le prochain numéro. Vous connaissiez le premier chiffre grâce à votre connaissance de certains nombres cubiques. Pour le chiffre suivant, estimez un nombre entre 0 et 9 en fonction de l`endroit où votre nombre cible se situe entre les deux nombres limites.

3. Testez votre estimation en déterminant son cube. Essayez de multiplier l`estimation avec laquelle vous travaillez maintenant pour voir à quel point vous êtes proche du nombre cible.


4. Ajustez votre devis si nécessaire. Après avoir augmenté au cube de votre dernière estimation, vérifiez le résultat par rapport à votre nombre cible. Si le résultat est supérieur à la cible, votre estimation devrait être inférieure. Si le résultat est inférieur à l`objectif, vous devez l`ajuster vers le haut jusqu`à ce que vous atteigniez l`objectif.
 plus grand que la cible (600). Donc vous réduisez l`estimation à 8,4. Prenez le cube de ce nombre et comparez-le à votre cible. tu verras ça
plus grand que la cible (600). Donc vous réduisez l`estimation à 8,4. Prenez le cube de ce nombre et comparez-le à votre cible. tu verras ça  . C`est maintenant inférieur à votre objectif. Cela vous indique que la racine cubique de 600 doit être d`au moins 8,4, mais inférieure à 8,5.
. C`est maintenant inférieur à votre objectif. Cela vous indique que la racine cubique de 600 doit être d`au moins 8,4, mais inférieure à 8,5.
5. Estimez le nombre suivant pour une réponse plus précise. Continuez cette procédure d`estimation des nombres de 0 à 9, jusqu`à ce que votre réponse soit aussi précise que vous le souhaitez. Pour chaque tour d`estimation, commencez par vérifier la position de votre dernier calcul entre les nombres limites.
 , tandis que
, tandis que  . La cible (600) est légèrement plus proche de 592 que de 614. Estimez-vous donc le prochain nombre un peu moins qu`à mi-chemin entre 0 et 9. Un bon choix est 4, ce qui vous donnera une estimation de la racine cubique de 8,44.
. La cible (600) est légèrement plus proche de 592 que de 614. Estimez-vous donc le prochain nombre un peu moins qu`à mi-chemin entre 0 et 9. Un bon choix est 4, ce qui vous donnera une estimation de la racine cubique de 8,44.
6. Continuez à estimer et à ajuster Faites cela autant de fois que nécessaire, augmentez votre estimation au cube et voyez comment elle se compare au nombre cible. Recherchez les nombres qui sont juste en dessous ou juste au-dessus du nombre cible.
 . C`est juste au-dessus de la cible, alors lâchez-en et testez 8.43. Cela donne
. C`est juste au-dessus de la cible, alors lâchez-en et testez 8.43. Cela donne  à la suite. Vous savez donc que la racine cubique de 600 est un peu plus de 8,43 et un peu moins de 8,44.
à la suite. Vous savez donc que la racine cubique de 600 est un peu plus de 8,43 et un peu moins de 8,44.
sept. Continuez jusqu`à atteindre la précision souhaitée. Continuez à estimer, comparer et ré-estimer, aussi longtemps que nécessaire, jusqu`à ce que votre solution soit aussi précise que vous le souhaitez. Notez qu`avec chaque décimale, vos nombres cibles se rapprochent de plus en plus du nombre réel.
 si le résultat est inférieur de 0,1 à la réponse réelle.
si le résultat est inférieur de 0,1 à la réponse réelle.Partie3 sur 3: Comprendre comment fonctionne ce calcul

1. Revoir le binôme de Newton. Pour comprendre pourquoi cet algorithme fonctionne pour déterminer les racines cubiques, vous devez d`abord penser à quoi ressemble le cube en tant que binôme. Vous avez probablement appris cela au lycée (et comme la plupart des gens, vous l`avez probablement oublié assez rapidement). Sélectionnez deux variables  et
et  pour représenter les unités. Ensuite, vous calculez le binôme de
pour représenter les unités. Ensuite, vous calculez le binôme de  pour les dizaines.
pour les dizaines.
 et
et  pour représenter les unités. Ensuite, vous calculez le binôme de
pour représenter les unités. Ensuite, vous calculez le binôme de  pour les dizaines.
pour les dizaines. - Utiliser le terme
pour créer une douzaine. Quelle que soit la note que vous choisissez
,
formera une douzaine. Par exemple, si
est 2 et
est 6, alors . devient
égal à 26.

2. Écrire le binôme dans un cube. Nous travaillons maintenant à rebours, en déterminant d`abord le cube, puis en voyant pourquoi la solution des racines cubiques fonctionne. Nous avons besoin des valeurs de  trouver. Vous le faites en vous entraînant
trouver. Vous le faites en vous entraînant  . C`est un calcul trop long à montrer ici, mais le résultat final est
. C`est un calcul trop long à montrer ici, mais le résultat final est  .
.
 trouver. Vous le faites en vous entraînant
trouver. Vous le faites en vous entraînant  . C`est un calcul trop long à montrer ici, mais le résultat final est
. C`est un calcul trop long à montrer ici, mais le résultat final est  .
.
3. Connaître le sens de la division longue. Notez que la méthode de calcul de la racine cubique fonctionne comme une division longue. Dans la division longue, vous voyez que deux facteurs se sont multipliés ensemble, donnez le nombre avec lequel vous avez commencé. Dans ce calcul, le nombre que vous recherchez (le nombre qui se termine au-dessus du radical) est la racine cubique. Cela signifie qu`il est égal au terme (10A+B). Les véritables A et B ne sont plus pertinents maintenant, tant que vous comprenez la relation avec la réponse.

4. Voir la version étendue. Quand vous regardez le binôme de Newton, vous voyez pourquoi l`algorithme de racine cubique est correct. Voyez comment le diviseur à chaque étape de l`algorithme est égal à la somme des quatre termes que vous devez calculer et additionner. Ces termes se présentent comme suit :
 .) N`oubliez pas que lors du calcul de la racine cubique, le premier chiffre de chaque étape a été multiplié par 0300.
.) N`oubliez pas que lors du calcul de la racine cubique, le premier chiffre de chaque étape a été multiplié par 0300.
5. Regardez la précision grandir. En travaillant sur une longue division, chaque étape que vous effectuez donne une grande précision à votre réponse. Par exemple, l`exemple de problème élaboré dans cet article consiste à déterminer la racine cubique de 10. Dans la première étape, la solution est 2, car  se rapproche, mais est inférieur à 10. En réalité,
se rapproche, mais est inférieur à 10. En réalité,  . Après le deuxième tour, votre solution est 2.1. Une fois que vous aurez réglé cela, vous obtiendrez
. Après le deuxième tour, votre solution est 2.1. Une fois que vous aurez réglé cela, vous obtiendrez , et c`est beaucoup plus proche du résultat souhaité (10). Après le troisième tour, vous avez 2,15, et cela vous donne
, et c`est beaucoup plus proche du résultat souhaité (10). Après le troisième tour, vous avez 2,15, et cela vous donne  . Continuez à travailler en groupes de trois nombres et vous obtiendrez une réponse aussi précise que vous le souhaitez.
. Continuez à travailler en groupes de trois nombres et vous obtiendrez une réponse aussi précise que vous le souhaitez.
 se rapproche, mais est inférieur à 10. En réalité,
se rapproche, mais est inférieur à 10. En réalité,  . Après le deuxième tour, votre solution est 2.1. Une fois que vous aurez réglé cela, vous obtiendrez
. Après le deuxième tour, votre solution est 2.1. Une fois que vous aurez réglé cela, vous obtiendrez , et c`est beaucoup plus proche du résultat souhaité (10). Après le troisième tour, vous avez 2,15, et cela vous donne
, et c`est beaucoup plus proche du résultat souhaité (10). Après le troisième tour, vous avez 2,15, et cela vous donne  . Continuez à travailler en groupes de trois nombres et vous obtiendrez une réponse aussi précise que vous le souhaitez.
. Continuez à travailler en groupes de trois nombres et vous obtiendrez une réponse aussi précise que vous le souhaitez.Des astuces
- Comme tout, vos compétences en mathématiques s`amélioreront avec la pratique. Plus vous pratiquez, mieux vous serez capable de faire ce genre de calculs.
Mises en garde
- C`est facile de se tromper ici. Vérifiez soigneusement votre travail et recommencez l`élaboration.
Nécessités
- Stylo ou crayon
- Papier
- Règle
- La gomme
Articles sur le sujet "Calculer les racines cubiques à la main"
Оцените, пожалуйста статью
Populaire