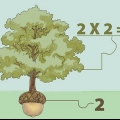
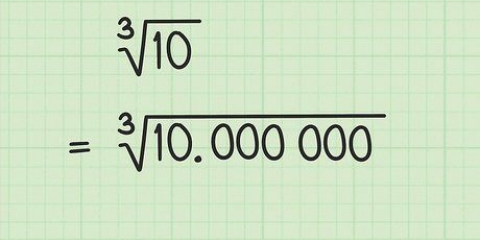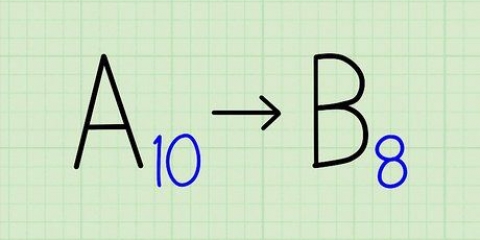Dans notre exemple on prend les racines carrées de 25 et 16. Voir ci-dessous: Carré (25×16) Carré (25) × Carré (16) 5 × 4 = 20 
Prenons la racine carrée de 147 comme exemple. 147 n`est pas le produit de deux carrés parfaits, nous ne pouvons donc pas obtenir une belle valeur entière. Mais c`est le produit d`un carré parfait et d`un autre nombre - 49 et 3. Nous pouvons utiliser ces informations pour écrire notre réponse dans les termes les plus simples : carré (147) = Sqrt (49 × 3) = Sqrt(49) × Sqrt(3) = 7 × carré(3) 
Revenons à notre exemple. Puisque 2 = 4 et 1 = 1, nous savons que Sqrt(3) est compris entre 1 et 2 – probablement plus proche de 2 que de 1. Nous estimons que 1,7. 7 × 1,7 = 11.9. En vérifiant cela avec la calculatrice, nous voyons que nous sommes assez proches de la réponse : 12.13. Cela fonctionne également pour les plus grands nombres. Par exemple, Sqrt(35) est à peu près entre 5 et 6 (probablement plus proche de 6). 5 = 25 et 6 = 36. 35 est entre 25 et 36, donc la racine carrée sera entre 5 et 6. Puisque 35 est juste en dessous de 36, nous pouvons dire avec une certaine confiance que sa racine carrée juste est inférieur à 6. Vérifier avec une calculatrice nous donne une réponse d`environ 5,92 - nous avions raison. 
Un exemple : nous déterminons la racine carrée de 45 en utilisant cette méthode. On sait que 45 = 9 × 5 et que 9 = 3 × 3. On peut donc écrire la racine carrée comme ceci : Sqrt(3 × 3 × 5). Supprimez simplement les 3 et placez un 3 à l`extérieur du radical pour obtenir une racine carrée simplifiée : (3)Sqrt(5). Maintenant, vous pouvez facilement estimer. Un dernier exemple ; on détermine la racine carrée de 88 : carré(88) = Carré (2 × 44) = Sqrt (2 × 4 × 11) = Sqrt (2 × 2 × 2 × 11). Nous avons plusieurs 2 dans notre racine carrée. Puisque 2 est premier, nous pouvons supprimer une paire et placer un 2 en dehors de la racine carrée. = Notre racine carrée en termes les plus simples est (2) Sqrt(2 × 11) ou (2) Carré(2) Carré(11). Maintenant, nous pouvons approcher Sqrt(2) et Sqrt(11) et trouver une réponse estimée, si nous voulions. 

Dans notre exemple, le chiffre le plus à gauche est le chiffre 7. Parce que nous savons que 2 = 4 7 < 3 = 9, on peut dire que n = 2 car c`est le plus grand entier dont le carré est inférieur ou égal à 7. Écrivez 2 dans le quadrant supérieur droit. C`est le premier chiffre de la réponse. Écrivez 4 (le carré de 2) dans le quadrant inférieur droit. Ce numéro est important pour la prochaine étape. 
Dans notre exemple, nous écrivons un 4 sous 7 et le soustrayons. Cela donne 3 comme réponse. 
Dans notre exemple, le nombre suivant est "80". Remarque "80" à côté du 3 dans le quadrant gauche. Multipliez ensuite le nombre en haut à droite par 2. Ce nombre est 2, donc 2 × 2 = 4. Remarque "`4"` en bas à droite, suivi de _×_=. 
Dans notre exemple, nous remplissons 8, ce qui donne 4(8) × 8 = 48 × 8 = 384. C`est supérieur à 380. Donc 8 est trop gros, mais 7 ne l`est probablement pas. Complétez 7 et résolvez : 4(7) × 7 = 329. 7 est bon car 329 est plus petit que 380. Remarque 7 en haut à droite. C`est le deuxième chiffre de la racine carrée de 780,14. 
Dans notre exemple, nous soustrayons 329 de 380, et cela donne 51 à la suite. 
Dans notre réponse, nous écrivons maintenant une virgule car nous la rencontrons également dans 780.14. Déplacez la paire suivante (14) vers le bas dans le quadrant gauche. 27 x 2 = 54, donc on écrit "54 _×_=" dans le quadrant inférieur droit. 
Dans notre exemple, 549 × 9 = 4941, ce qui est inférieur ou égal au nombre de gauche (5114). 549 × 10 = 5490, ce qui est trop élevé, donc 9 est notre réponse. Écrivez 9 comme nombre suivant en haut à droite et soustrayez le résultat de la multiplication du nombre de gauche : 5114 -4941 = 173. 
Calculer la racine carrée d'un nombre sans calculatrice
Teneur
Avant l`avènement des calculatrices, les étudiants et les professeurs devaient calculer les racines carrées avec un stylo et du papier. Diverses techniques ont été développées à l`époque pour s`attaquer à cette tâche parfois lourde, certaines donnant une estimation approximative et d`autres calculant la valeur exacte. Lisez la suite pour apprendre à trouver la racine carrée d`un nombre en quelques étapes faciles.
Pas
Méthode 1 sur 2: Enracinement avec des facteurs premiers

1. Divisez votre nombre en carrés. Cette méthode utilise les facteurs d`un nombre pour trouver la racine carrée d`un nombre (selon le nombre, cela peut être une réponse exacte ou une estimation). le les facteurs d`un nombre donné sont une séquence aléatoire de nombres multipliés ensemble pour former ce nombre particulier. Par exemple, vous pouvez dire que les facteurs de 8 sont égaux à 2 et 4 car 2 × 4 = 8. Les carrés parfaits, en revanche, sont des nombres entiers qui sont le produit d`autres nombres entiers. Par exemple : 25, 36 et 49 sont des carrés parfaits car ils sont égaux à 5, 6 et 7 . respectivement. Les seconds facteurs de puissance sont, vous l`aurez compris, des facteurs qui sont aussi des carrés parfaits. Pour trouver une racine carrée en utilisant des facteurs premiers, essayez d`abord de diviser le nombre en ses facteurs cubiques.
- Prenons l`exemple suivant. On va trouver la racine carrée de 400. Pour commencer, nous divisons le nombre en carrés. Puisque 400 est un multiple de 100, nous savons qu`il est divisible par 25 - un carré parfait. La mémorisation rapide nous dit que 400 / 25 = 16. 16 se trouve aussi être un carré parfait. Donc les facteurs quadratiques de 400 sont 25 et 16 car 25 × 16 = 400.
- Nous écrivons ceci comme : Sqrt(400) = Sqrt (25 × 16)

2. Prenez les racines carrées de vos racines carrées. La règle du produit des racines carrées stipule que pour un nombre donné une et b, Sqrt(a × b) = Sqrt(a) × Sqrt(b). En raison de cette propriété, nous pouvons maintenant prendre les racines carrées des facteurs cubiques et les multiplier ensemble pour la réponse.

3. Si votre nombre ne peut pas être factorisé tout à fait parfaitement, simplifiez-le. En réalité, les nombres dont vous voulez trouver les racines carrées ne seront pas de beaux nombres arrondis avec de belles racines carrées comme 400. Dans ces cas, il peut ne pas être possible d`obtenir un nombre entier comme réponse. Au lieu de cela, en utilisant tous les cubes que vous pouvez trouver, vous pouvez déterminer la réponse sous la forme d`une racine carrée plus petite et plus facile à utiliser. Pour ce faire, réduisez le nombre à une combinaison de facteurs de cube et d`autres facteurs, puis en le simplifiant.

4. Simplifier, si nécessaire. En utilisant la racine carrée dans les termes les plus simples, il est généralement assez facile d`obtenir une estimation approximative de la réponse en estimant les racines carrées restantes et en les multipliant. Une façon d`améliorer vos suppositions est de trouver les carrés parfaits de chaque côté du nombre dans votre racine carrée. Vous savez que la valeur décimale du nombre dans votre racine carrée se situe quelque part entre ces deux nombres, donc votre estimation devrait également se situer entre ces nombres.

5. Alternativement, dans un premier temps, vous pouvez simplifier le nombre aumultiple moins commun. La recherche de facteurs carrés n`est pas nécessaire si vous pouvez facilement trouver les facteurs premiers d`un nombre (facteurs qui sont également premiers en même temps). Écrivez le nombre en termes de plus petits multiples communs. Recherchez ensuite parmi vos facteurs les paires correspondantes de nombres premiers. Si vous trouvez deux facteurs premiers qui correspondent, supprimez-les de la racine carrée et mettez une de ces nombres en dehors du radical.
Méthode 2 sur 2: Trouver des racines carrées sans calculatrice
Avec une longue division

1. Divisez les chiffres de votre numéro en paires. Cette méthode est similaire à la division longue, qui vous permet de exact trouver la racine carrée d`un nombre chiffre par chiffre. Bien que cela ne soit pas essentiel, diviser un nombre en morceaux exploitables peut le rendre plus facile à résoudre, surtout s`il est long. Tracez d`abord une ligne verticale divisant la zone de travail en 2 zones, puis une ligne plus courte près du haut de la zone de droite, en la divisant en une partie supérieure plus petite et une partie plus grande en dessous. Divisez ensuite le nombre en paires de nombres, en commençant par la virgule décimale. Selon cette règle, 79520789182.47897 devient égal à "7 95 20 78 91 82,47 89 70". Écrivez ce numéro dans la zone en haut à gauche.
- A titre d`exemple, calculons la racine carrée de 780,14. Divisez votre espace de travail comme indiqué ci-dessus et notez "7 80, 14" dans le coin supérieur gauche. Ce n`est pas grave s`il n`y a qu`un seul chiffre à l`extrême gauche, au lieu de deux. Vous écrivez ensuite la réponse (la racine carrée de 780,14) en haut de la zone de droite.

2. Trouver le plus grand entier m dont le carré est inférieur ou égal au chiffre ou au nombre le plus à gauche. Trouvez le plus grand carré inférieur ou égal à ce nombre, puis trouvez la racine carrée de ce carré. Ce numéro est m. Notez que dans la zone en haut à droite et écrivez le carré de n dans le quadrant inférieur de cette zone.

3. Soustraire le nombre que vous avez calculé du chiffre ou du nombre le plus à gauche. Comme pour la division longue, l`étape suivante consiste à soustraire le carré du nombre que nous venons d`utiliser pour calculer. Écrivez ce nombre sous le nombre le plus à gauche et soustrayez-les les uns des autres. Écrivez la réponse ci-dessous.

4. Déplacer le numéro suivant vers le bas. Placez-le à côté de la valeur que vous avez trouvée dans l`édition précédente. Multipliez le nombre en haut à droite par deux et notez-le en bas à droite. Économisez de l`espace à côté du nombre que vous venez d`écrire pour la somme de multiplication que vous ferez à l`étape suivante. Ecrire ici `"_×_="`.

5. Entrez les chiffres à droite. Dans l`espace vide de la somme (à droite), entrez le plus grand entier qui rendra le résultat de la somme de multiplication à droite inférieur ou égal au nombre actuel à gauche.

6. Soustrayez le nombre que vous venez de calculer du nombre actuel sur la gauche. Donc, vous soustrayez le résultat de la multiplication à droite de la réponse actuelle à gauche. Écrivez votre réponse directement ci-dessous.

sept. Répétez l`étape 4. Déplacez la prochaine paire de nombres de 780,14 vers le bas. Si vous arrivez à une virgule, écrivez cette virgule dans la réponse à droite. Multipliez ensuite le nombre en haut à droite par 2 et écrivez la réponse à côté de ("_ × _") comme ci-dessus.

8. Répétez les étapes 5 et 6. Trouvez le plus grand nombre qui donne une réponse inférieure ou égale au nombre actuel sur la gauche. Résoudre.

9. Pour rendre le résultat précis, répétez la procédure précédente jusqu`à ce que vous trouviez la réponse avec le nombre de décimales (centièmes, millièmes) dont vous avez besoin.
Comprendre la procédure
- Notez que si vous divisez 88962 par 7 en utilisant la division longue, la première étape est la même : vous avez affaire au premier chiffre de 88962 (8) et vous voulez que le plus grand chiffre multiplié par 7 soit inférieur ou égal à 8. Essentiellement, vous décidez ré de sorte que 7×d 8 < 7×(j+1). Dans ce cas d est égal à 1.
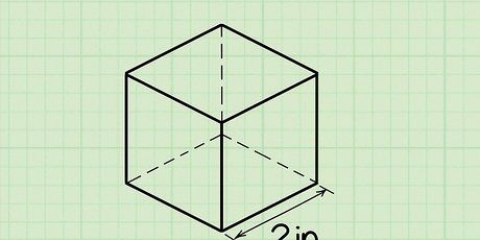
- Dans notre exemple (10A+B)² = L = S = 100A² + 2×10A×B + B². Rappelez-vous que 10A+B représente notre réponse L avec B dans la position des unités et A dans la position des dizaines. Par exemple, si A=1 et B=2, alors 10A+B est le nombre 12. (10A+B)² est l`aire de tout le carré, tandis que 100A² est l`aire du plus grand carré intérieur, B² est l`aire des moindres carrés et 10A × B est l`aire de chacun des rectangles restants. Grâce à cette procédure longue et compliquée, nous pouvons trouver l`aire de tout le carré en ajoutant les aires des carrés et des rectangles qui le composent.

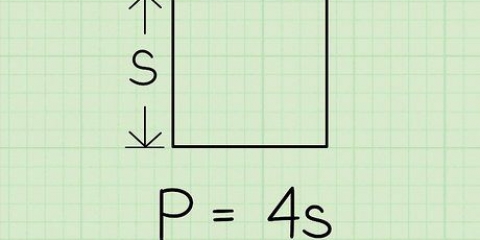
1. Considérez le nombre dont vous voulez calculer la racine carrée comme l`aire S d`un carré. Puisque l`aire d`un carré est L, où L est la longueur d`un de ses côtés, donc en prenant la racine carrée de votre nombre, vous essayez de calculer la longueur L du côté de ce carré.

2. Donnez à chaque chiffre de votre réponse une lettre. Donnez la variable A comme premier chiffre de L (la racine carrée que nous essayons de calculer). B est le deuxième chiffre, C est le troisième, et ainsi de suite.

3. Donnez une lettre à chacun "paire de nombres" du nombre avec lequel vous commencez. Donner la variable Sune à la première paire de chiffres de S (la valeur initiale), Sb à la deuxième paire de chiffres, etc.

4. Comprendre la relation entre cette méthode et la division longue. Cette méthode pour trouver une racine carrée est essentiellement une division longue, divisant la valeur initiale par sa racine carrée et prenant la racine carrée comme réponse "données". Comme pour la division longue, où vous ne vous intéressez qu`au chiffre suivant à la fois, vous ne vous intéressez qu`aux deux chiffres suivants à la fois (qui correspondent au chiffre suivant de la racine carrée).

5. Trouver le plus grand nombre dont le carré est inférieur ou égal à Sune est. Le premier chiffre A de notre réponse est alors le plus grand entier dont le carré n`est pas supérieur à Sune (A tel que A² Sa < (A+1)²). Dans notre exemple, S. estune = 7 et 2² 7 < 3², donc A = 2.

6. Visualisez le carré dont vous voulez trouver l`aire. Votre réponse, la racine carrée de la valeur initiale, est L, décrivant la longueur d`un carré d`aire S (la valeur initiale). Les valeurs pour A, B et C représentent les nombres dans la valeur L. Une autre façon de dire cela est que pour une réponse à 2 chiffres, 10A + B = L, et pour une réponse à 3 chiffres, 100A + 10B + C = L, et ainsi de suite.

sept. Soustraire A² de Sune. Apportez une paire de nombres (Sb) à partir du nombre S. sune sb est presque l`aire totale du carré, dont vous venez de soustraire l`aire du plus grand carré intérieur. Le reste est disons le nombre N1, que nous avons obtenu à l`étape 4 (N1 =380 dans notre exemple). N1 est égal à 2×10A×B + B² (l`aire des 2 rectangles plus l`aire du petit carré).

8. Regardez N1 = 2×10A×B + B², également écrit N1 = (2×10A + B) × B. Dans notre exemple, vous connaissez déjà N1 (380) et A (2), vous devez donc maintenant trouver B. B n`est probablement pas un entier, vous avez donc besoin réellement trouver le plus grand entier B, tel que (2×10A + B) × B ≤ N1. Donc maintenant vous avez : N1 < (2×10A + (B+1)) × (B+1).)

9. Résous l`équation. Pour résoudre cette équation, multipliez A par 2, décalez-le aux dizaines (multipliez par 10), placez B dans les unités et multipliez le résultat par B. En d`autres termes, (2×10A + B) × B. C`est exactement ce que tu fais quand tu écris "N_×_=" (avec N=2×A) dans le quadrant inférieur droit à l`étape 4. À l`étape 5, vous déterminez le plus grand nombre entier B qui passe sous la ligne, tel que (2×10A + B) × B ≤ N1.

dix. Soustraire l`aire (2×10A + B) × B de l`aire totale. Cela donne l`aire S-(10A+B)² que vous n`avez pas encore prise en compte (et que vous utilisez pour calculer les nombres suivants de la même manière).

11. Pour calculer le chiffre suivant C, répétez la procédure. Déplacez la prochaine paire de nombres de S vers le bas (Sc) pour obtenir N2 sur la gauche, et recherchez le plus grand C. Vous avez maintenant : (2×10×(10A+B)+C) × C ≤ N2 (égal à deux fois le nombre à deux chiffres "UN B" suivie par "_×_=" . Déterminez maintenant le plus grand nombre que vous pouvez entrer ici, ce qui vous donnera une réponse inférieure ou égale à N2.
Des astuces
- Déplacer la virgule décimale de deux places (un facteur 100) déplace la virgule décimale dans la racine carrée correspondante d`une place (un facteur 10).
- Dans l`exemple, 1,73 peut être considéré comme "du repos": 780,14 = 27,9² + 1,73.
- Cette méthode fonctionne pour n`importe quel système numérique, pas seulement le système décimal (dix décimales).
- N`hésitez pas à mettre les calculs où vous voulez. Certaines personnes l`écrivent au-dessus du nombre dont elles veulent calculer la racine carrée de.
- Une méthode alternative est la suivante : √z = √(x^2+y) = x + y/(2x + y/(2x + y/(2x + ...))). Par exemple, pour calculer la racine carrée de 780,14, vous prendriez l`entier au carré le plus proche de 780,14 (28), donc =780,14, x=28 et y=-3,86. Remplir et estimer nous donne x + y/(2x) et cela donne (termes simplifiés) 78207/2800 soit environ 27 931(1) ; le prochain terme, 4374188/156607 ou environ 27.930986(5). Chaque terme ajoute environ 3 décimales de précision au précédent.
Mises en garde
- Assurez-vous de diviser le nombre en paires à partir de la virgule décimale. Diviser 79520789182.47897 comme "79 52 07 89 18 2.4 78 97" donne un résultat qui n`est pas correct.
Articles sur le sujet "Calculer la racine carrée d'un nombre sans calculatrice"
Оцените, пожалуйста статью
Populaire