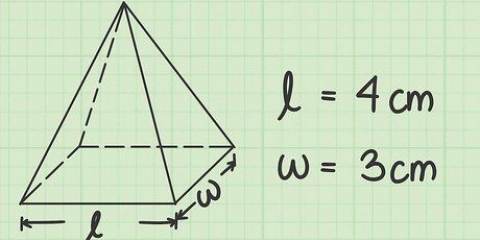Ce processus est fondamentalement le même que de calculer d`abord l`aire de la base, puis de multiplier cette aire par la hauteur du cube (ou en d`autres termes longueur × largeur × hauteur), car la surface de la base est déterminée en multipliant la longueur par la largeur. Puisque la longueur, la largeur et la hauteur d`un cube sont égales, nous pouvons simplifier le processus en élevant l`une de ces valeurs à la troisième puissance. Continuons avec notre exemple. La longueur du bord était de 2 cm, donc le volume du cube est de 2 x 2 x 2 (ou 2)= 8. 
Dans notre exemple, la longueur de la côte a été donnée en centimètres, la réponse doit donc être indiquée en centimètres cubes. Alors la réponse est 8cm. 

Donc dans notre exemple on divise cinquante par six : 50/6 = 8,33 cm. Rappelez-vous que les unités des réponses bidimensionnelles sont écrites au carré (cm, m et ainsi de suite). 
Dans notre exemple, √8.33 = 2,89 cm. 
Donc dans notre exemple : 2,89 × 2,89 × 2,89 = 24,14 cm. N`oubliez pas d`écrire la réponse en unités cubes. 

Cela peut aussi être déduit du théorème de Pythagore. ré, ré et je forment un triangle équilatéral avec D comme hypoténuse, donc ré = ré + je. Auparavant, nous avions déjà déterminé : ré = 2je, donc on peut aussi dire ce qui suit : ré = 2je + je = 3je. Supposons que nous sachions que la longueur de la diagonale allant d`un coin de la base du cube au coin opposé de la face supérieure du cube est de 10 mètres. Donc, si nous voulons calculer le volume, nous entrons 10 dans la formule ci-dessus pour ré. ré = 3je. 10 = 3je. 100 = 3je 33.33 = je 5.77 mètres = je. A partir de ce point, nous pouvons calculer le volume en augmentant la longueur de la nervure au cube. 5.77 = 192.45 mètres
Calculer le volume d'un cube
Teneur
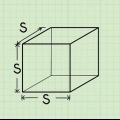
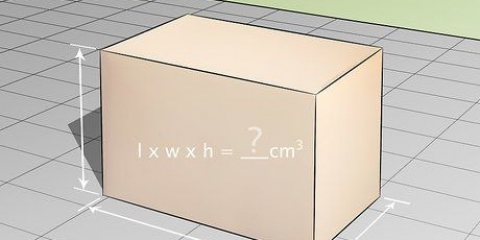
Un cube est une figure en trois dimensions dont la longueur, la largeur et la hauteur sont égales. Un cube a six faces carrées dont les côtés sont de même longueur et perpendiculaires les uns aux autres. Le calcul du volume d`un cube est très simple - il suffit généralement de multiplier les éléments suivants : longueur × largeur × hauteur. Étant donné que les arêtes d`un cube ont toutes la même longueur, vous pouvez également voir le volume d`un cube comme suit : je, par lequel je est la longueur de l`une des arêtes du cube. Allez à l`étape 1 pour une explication détaillée.
Pas
Méthode 1 sur 3: Élever le bord du cube au cube

1. Trouver la longueur d`une des arêtes du cube. Souvent vous verrez une somme où la longueur d`une des côtes est déjà donnée. Une fois que vous avez ces informations, vous avez tout ce qu`il faut pour déterminer le volume du cube. Utilisez une règle ou un ruban à mesurer si vous ne résolvez pas un problème mathématique, mais souhaitez simplement connaître le volume d`un objet existant en forme de cube.
- Pour mieux comprendre le processus de détermination du volume d`un cube, commençons par un exemple de somme en parcourant les étapes de cette section. Supposons que l`arête du cube 2 cm c`est long. Nous allons utiliser ces informations dans l`étape suivante pour déterminer le volume du cube.

2. Augmenter la longueur de la côte à la troisième puissance. Une fois que vous avez la longueur d`une des côtes, augmentez ce nombre à la troisième puissance. En d`autres termes, multipliez le nombre deux fois par lui-même. si je est la longueur de la côte, alors vous multipliez je × je × je (ou sous une forme plus simple je). Le résultat est le volume du cube.

3. Donnez votre réponse en unités cubes. Le volume est la mesure d`un espace tridimensionnel, donc la solution doit être écrite en unités cubiques. Sur un test, cela peut vous coûter des points si vous n`indiquez pas correctement la réponse en unités cubes, alors n`oubliez pas!
Méthode 2 sur 3: Détermination du volume par surface

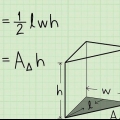
1. Trouvez l`aire des faces de votre cube. le le plus simple moyen de déterminer le volume est d`élever la nervure au cube, mais ce n`est pas le quelconque chemin. La longueur de l`arête d`un cube ou l`aire de l`une de ses faces peut être dérivée de plusieurs autres propriétés du cube, ce qui signifie que si vous commencez avec cette information, vous pouvez déterminer le volume du cube de manière dérivée. Par exemple, si vous ne connaissez que l`aire totale de tous les côtés du cube, vous pouvez trouver le volume en divisant cette aire par six, puis en prenant la racine carrée de ce nombre pour trouver la longueur de l`arête. À partir de ce point, vous pouvez à nouveau augmenter à la troisième puissance. Dans cette section, nous parcourons ce processus étape par étape.
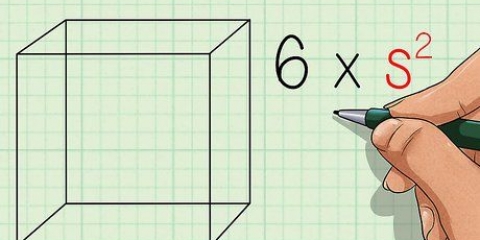
- L`aire d`un cube est donnée par la formule 6je, par lequel je est la longueur de l`une des arêtes du cube. Cette formule revient en fait à déterminer l`aire bidimensionnelle de l`un des côtés du cube, puis à additionner les six aires (égales). Nous utiliserons cette formule pour déterminer le volume du cube à partir de l`aire du cube.
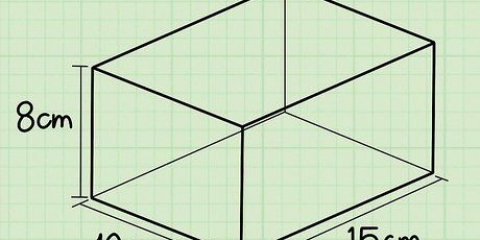
- Supposons que nous ayons un cube dont nous savons que l`aire 50cm est, mais nous ne savons pas quelle est la longueur des côtes. Dans les prochaines étapes, nous utiliserons ces informations pour trouver le volume du cube.

2. Divisez l`aire du cube par six. Puisque le cube a six faces d`aire égale, on peut déterminer l`aire d`une face en divisant l`aire du cube par six. L`aire d`un plan est la même que la multiplication de deux arêtes (l × b, b × h ou h × l).

3. Trouver la racine carrée de cette valeur. Puisque l`aire de l`une des faces d`un cube est égale à je (je × je), nous pouvons maintenant prendre la racine carrée de la valeur trouvée pour déterminer la longueur d`une des nervures. Une fois que vous savez cela, vous avez suffisamment d`informations pour calculer le volume du cube comme d`habitude.

4. Augmentez ce nombre à la troisième puissance pour trouver le volume du cube. Maintenant que vous avez déterminé une valeur pour la longueur des nervures, vous pouvez augmenter ce nombre au cube pour déterminer le volume comme décrit dans la première section de cet article.
Méthode 3 sur 3: Détermination du volume à l`aide de diagonales

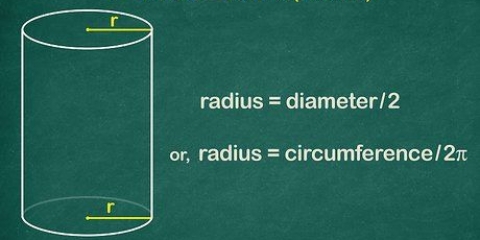
1. Divisez la diagonale de l`une des faces du cube par 2 pour trouver la longueur des arêtes du cube. La diagonale d`un carré est √2 × la longueur de l`une de ses arêtes. Autrement dit, si vous ne connaissez que la valeur d`une des diagonales d`une face du cube, vous pouvez calculer la longueur des arêtes du cube en divisant cette valeur par √2. À partir de ce point, vous pouvez à nouveau monter à la troisième puissance et déterminer le volume comme décrit ci-dessus.
- Supposons que l`une des faces du cube a une diagonale de7 mètres long. Ensuite, nous pouvons calculer la longueur d`une des côtes en divisant 7 par √2. 7/√2 = 4,96 mètres. Maintenant que nous connaissons la longueur des arêtes du cube, nous pouvons calculer le volume du cube en élevant 4,96 au cube : 4,96 = 122,36 mètres.
- Faites attention: ré = 2je, vrai ré est la longueur de la diagonale de l`une des faces du cube et je est la longueur de l`une des arêtes du cube. Cela peut être dérivé du théorème de Pythagore, où le carré de l`hypoténuse d`un triangle équilatéral est égal à la somme du carré des deux autres côtés. Puisque la diagonale d`une face d`un cube forme un triangle équilatéral avec deux des arêtes de cette face, nous pouvons dire ce qui suit : ré = je + je = 2je.

2. Trouvez le carré de la diagonale entre deux coins opposés du cube, divisez par trois et prenez la racine carrée pour trouver la longueur d`un des bords. Si la longueur de la ligne tridimensionnelle entre deux coins opposés du cube est la seule donnée, vous pouvez toujours déterminer le volume du cube. ré forme l`un des côtés d`un triangle équilatéral dont l`hypoténuse est la ligne entre deux coins opposés du cube, on peut donc dire : ré = 3je, où D est la ligne tridimensionnelle entre deux coins opposés du cube.
Articles sur le sujet "Calculer le volume d'un cube"
Оцените, пожалуйста статью
Populaire