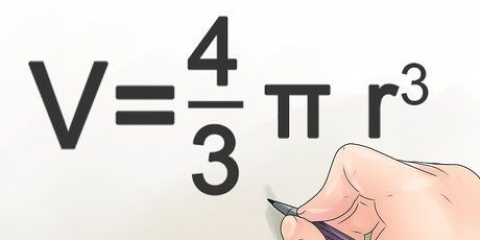Pour trouver s³, multipliez s trois fois par lui-même : s³ = s x s x s 
Si vous n`êtes pas sûr à 100% si votre forme est un cube, mesurez tous les côtés pour voir s`ils sont identiques. Si ce n`est pas le cas, vous devrez utiliser la méthode ci-dessous pour calculer le volume d`un faisceau. Remarque : Dans les exemples d`images, les mesures sont données en pouces (pouces), mais nous utilisons des centimètres (cm). 




Exemple : La longueur de cette poutre est de 4 cm, donc l = 4 cm. Ne vous inquiétez pas trop de quel côté est la longueur, etc. Tant que vous ne mesurez que trois côtés différents, le résultat sera le même. 
Exemple : La largeur de cette poutre est de 3 cm, donc b = 3 cm. Si vous mesurez le faisceau avec une règle ou un ruban à mesurer, n`oubliez pas de tout noter dans la même unité de mesure. 
Exemple : La hauteur de cette barre est de 6 cm, donc h = 6 cm. 
Dans cet exemple, l = 4, b = 3 et h = 6. Par conséquent, le résultat est V = 4 x 3 x 6 = 72. 
Par exemple, si les dimensions de la poutre étaient en mètres, vous obtiendriez l = 2 m, l = 4 m et h = 8 m. Le volume serait alors de 2 m x 4 m x 8 m = 64 m³. 

Dans la plupart des cas, il suffit d`arrondir pi à 3,14. Demandez à votre professeur ce qu`il veut. La formule pour trouver le volume d`un cylindre est en fait très similaire à celle du volume d`une poutre : vous multipliez la hauteur de la forme par l`aire de la base. Pour une poutre, l`aire de la base est l x b, pour un cylindre c`est π x r², l`aire d`un cercle de rayon r. 

Une autre option consiste à mesurer la circonférence du cercle (la distance qui l`entoure) avec un morceau de ficelle ou un ruban à mesurer. Mettez ensuite le résultat dans cette formule : C (circonférence) est 2 x π x r. Divisez la circonférence par 2 x (6,28) et vous avez le rayon. Par exemple, si la circonférence que vous avez mesurée est de 8 cm, alors le rayon est de 1,27 cm. Si vous avez vraiment besoin d`une mesure exacte, vous pouvez utiliser l`une ou l`autre méthode pour voir si les résultats sont les mêmes. Si non, vérifiez à nouveau. La méthode de la circonférence donne généralement un résultat plus précis. 
Si le rayon est de 4 cm, alors l`aire du cercle est A = π x 4². 4² = 4 x 4, ou 16. 16 xπ = 16 x 3,14 = 50,24 cm². Si le diamètre de la base est connu, plutôt que le rayon, rappelez-vous que d = 2 x r. Ensuite, vous devez diviser le diamètre par deux pour trouver le rayon. 

V = x 4² x 10 x 4²= 50,24 50,24 x 10 = 502,4 V = 502,4 


La formule pour les pyramides droites, où le sommet est directement au-dessus du centre de la base, est la même que pour les pyramides inclinées, où le sommet n`est pas au centre. 
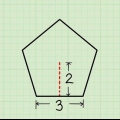
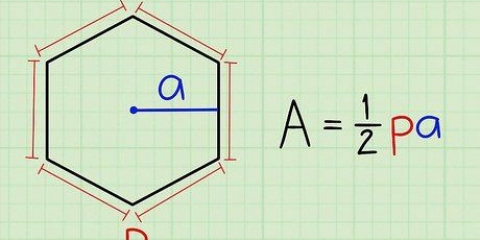
La formule pour l`aire d`un triangle est A = 1/2 x b x h, où b est la base et h est la hauteur. Il est possible de calculer l`aire de n`importe quel polygone régulier avec la formule A = 1/2 xpxa, où A est l`aire, p est le périmètre et a est l`apothème, qui est la distance du centre de la forme à le centre d`un des côtés. Vous pouvez également vous faciliter la tâche et utiliser un calculateur de polygones réguliers en ligne. 

Si on avait eu une autre pyramide avec une base d`une aire de 26 et une hauteur de 8, le résultat aurait été : 1/3 x 26 x 8 = 69,33. 


La partie π x r² fait référence à l`aire du cercle qui forme la base du cône. Ainsi, la formule du volume du cône est 1/3 x l x h, tout comme la formule de la pyramide de la méthode ci-dessus! 
Dans cet exemple le rayon est de 3 cm. Si nous mettons cela dans la formule, nous obtenons : A = π x 3². 3² = 3 x3, ou 9, donc A = π x 9. A = 28,27 cm². 


Dans notre exemple qui est 141,35 x 1/3 = 47,12, le volume du cône. Encore une fois : 1/3 x π x 3² x 5 = 47,12. 




Par exemple, si vous mesurez la balle et voyez que la circonférence est de 18 cm, divisez cela par 6,28, vous savez que le rayon est de 2,87 cm. Il peut être difficile de mesurer une sphère, il est donc préférable de la mesurer trois fois et de la moyenner (additionner les trois mesures ensemble et diviser par trois) pour obtenir la mesure aussi précise que possible. Par exemple, si vous avez mesuré trois fois et que les résultats étaient 18 cm, 17,75 cm et 18,2 cm, additionnez cela (18 + 17,5 + 18,2 = 53,95) et divisez par 3 (53,95/3 = 17,98). Vous utilisez cette moyenne pour calculer le volume. 


Donc, dans notre exemple, cela devient 36 x 3,14 = 113,09. 
Calculer le volume
Teneur
Le volume d`une figure est l`espace tridimensionnel qu`elle occupe. Vous pouvez représenter le volume comme la quantité d`eau (ou d`air, de sable, etc.).) qui rentrerait dans le moule s`il était complètement plein. Les unités de mesure de volume couramment utilisées sont les centimètres cubes et les mètres cubes.Cet article vous apprendra à calculer le volume de six formes tridimensionnelles différentes couramment rencontrées dans les tests de mathématiques, notamment le cube, la sphère et le cône. Vous verrez qu`il existe de nombreuses similitudes qui vous permettront de vous souvenir facilement. Voyez si vous pouvez trouver ces correspondances!
Pas
Méthode 1 sur 6:Calculer le volume d`un cube

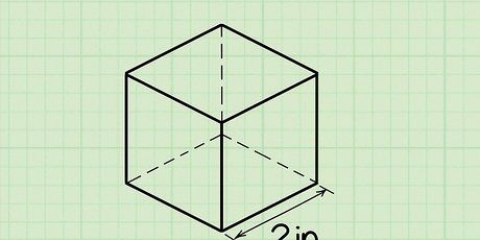
1. Reconnaître un cube. Un cube est une forme tridimensionnelle avec six faces carrées identiques.En d`autres termes, c`est une boîte avec des côtés égaux partout.
- Un dé est un bon exemple de cube que vous pourriez avoir à la maison. Les cubes de sucre ou les blocs pour enfants sont souvent aussi des cubes.

2. Apprenez la formule pour calculer le volume du cube. Puisque toutes les longueurs des côtés du cube sont de même longueur, la formule de calcul du volume du cube est très simple. L`endroit où les deux côtés se rencontrent s`appelle la côte. Nous abrégeons le volume en "V". Les côtes, ou la longueur du côté, on appelle ici "s". La formule devient alors V = s³

3. Trouver la longueur d`un côté du cube. Selon le devoir, cette information peut déjà être là, mais vous devrez peut-être aussi la mesurer vous-même avec une règle. Rappelez-vous, puisque c`est un cube, toutes les longueurs des côtés doivent être égales, donc peu importe celui que vous mesurez.

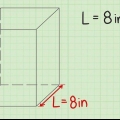
4. Mettez la longueur du côté dans la formule V = s³ et calculez-la. Par exemple, si vous mesuriez que la longueur du côté de votre cube est de 5 cm, vous écririez la formule comme suit : V = (5)³. 5 x 5 x 5 = 125 cm³, c`est donc le volume de votre cube!

5. Assurez-vous d`écrire votre réponse en centimètres cubes. Dans l`exemple ci-dessus, le cube a été mesuré en centimètres, donc la réponse doit être donnée en centimètres cubes. Si la longueur du côté du cube avait été de 3 mètres, alors le volume aurait été V = (3 m)³ = 27 m³.
Méthode 2 sur 6:Calculer le volume d`un faisceau.

1. Reconnaître un faisceau. Une poutre est une figure composée de six surfaces rectangulaires. C`est donc en fait un rectangle en trois dimensions, une sorte de boîte.
- En fait, un cube n`est qu`un faisceau spécial, où tous les côtés sont égaux.

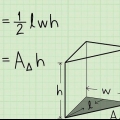
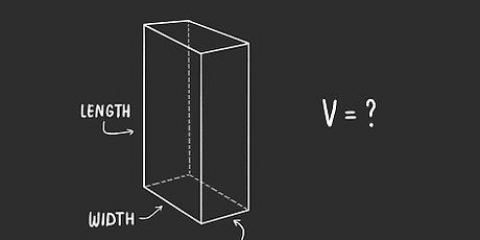
2. Apprendre la formule pour calculer le volume d`une poutre. La formule pour le volume d`une poutre est V = longueur (l) x largeur (l) x hauteur (h), ou V = l x l x h. Remarque : les images accompagnant ces exemples montrent "w" pour la largeur.

3. Trouver la longueur de la poutre. La longueur est le côté le plus long de la poutre qui est parallèle au sol ou à la surface sur laquelle elle repose. La longueur peut déjà être indiquée sur l`image, ou vous devrez peut-être la mesurer avec une règle.

4. Trouver la largeur du faisceau. La largeur du faisceau peut être trouvée en mesurant le petit côté qui est parallèle au sol ou à la surface sur laquelle il repose. Encore une fois, vérifiez d`abord si c`est déjà indiqué sur la photo, et mesurez-le sinon avec votre règle.

5. Trouver la hauteur de la poutre. La hauteur est la distance du sol ou de la surface sur laquelle repose la poutre jusqu`au sommet de la poutre. Voyez si c`est déjà indiqué sur la photo et mesurez-le différemment avec votre règle ou votre mètre ruban.

6. Entrez les dimensions dans la formule et calculez-la. Rappelez-vous que V = l x l x h.

sept. Assurez-vous d`écrire votre réponse en centimètres cubes. Le résultat est donc de 72 centimètres cubes, soit 72 cm³.
Méthode 3 sur 6: Calcul du volume d`un cylindre

1. Apprenez à identifier un cylindre. Un cylindre est une forme tridimensionnelle avec deux extrémités rondes identiques reliées par un seul côté incurvé. C`est en fait une tige droite et ronde.
- Une canette est un bon exemple de cylindre ou de pile AA.

2. Mémoriser la formule du volume d`un cylindre. Pour calculer le volume d`un cylindre, il faut connaître sa hauteur et le rayon de sa base circulaire.Le rayon est la distance entre le centre du cercle et le bord. La formule est V =π x r² x h, où V est le volume, r est le rayon, h est la hauteur et est la constante pi.

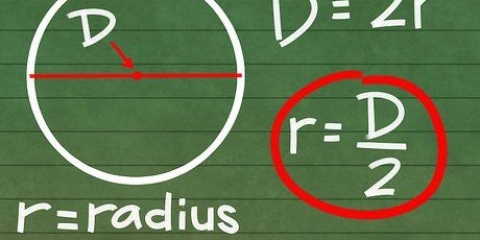
3. Trouver le rayon de la base. Si c`est déjà indiqué sur la photo, il suffit de le remplir. Si vous avez le diamètre au lieu du rayon, il suffit de le diviser par 2 pour trouver le rayon (d = 2 x r).

4. Mesurer la forme si le rayon n`est pas donné. Notez qu`il peut être difficile de mesurer le rayon exact d`un cercle. Une option consiste à mesurer le cercle à son point le plus large avec votre règle de haut en bas, en le divisant par deux.

5. Calculer l`aire du cercle à la base. Mettez le rayon dans la formule π x r². Multipliez le rayon par lui-même et multipliez ce résultat par. Par exemple:

6. Trouver la hauteur du cylindre. C`est simplement la distance entre les deux bases circulaires, ou la distance de la surface sur laquelle repose le cylindre jusqu`au sommet du cylindre. Voyez si la longueur est déjà indiquée dans l`image, ou mesurez-la différemment avec votre règle ou votre ruban à mesurer.

sept. Multipliez l`aire de la base par la hauteur du cylindre pour trouver le volume. Mettez les valeurs dans la formule V =π x r² x h. Dans notre exemple avec un rayon de 4 cm et une hauteur de 10 cm :

8. N`oubliez pas d`écrire votre réponse en centimètres cubes. Dans cet exemple, le cylindre a été mesuré en centimètres, la réponse doit donc être écrite en centimètres cubes : V = 502,4 cm³. Si le cylindre était mesuré en mètres, le volume devrait être écrit en mètres carrés (m³).
Méthode 4 sur 6: Calcul du volume d`une pyramide régulière

1. Savoir ce qu`est une pyramide régulière. Une pyramide est une forme tridimensionnelle avec un polygone à la base et des côtés effilés vers le haut (la pointe de la pyramide).Une pyramide régulière est une pyramide dont la base est un polygone régulier, ce qui signifie que tous les côtés et angles de ce polygone sont égaux.
- Habituellement, une pyramide est représentée avec une base carrée et des côtés effilés en pointe, mais la base d`une pyramide peut en fait avoir 5, 6 ou 100 côtés!
- Une pyramide avec un cercle comme base s`appelle un cône, dont nous discuterons dans la méthode suivante.

2. Apprenez la formule pour calculer le volume de la pyramide régulière. La formule pour le volume d`une pyramide régulière est V = 1/3 x b x h, où b est l`aire de la base et h est la hauteur de la pyramide, ou la distance verticale de la base au sommet.

3. Calculer l`aire de la base. La formule pour cela dépend du nombre de côtés de la base. Dans notre exemple, la base est un carré de 6 cm de côté. Rappelez-vous que la formule pour calculer l`aire d`un carré est A = s². Donc avec notre pyramide qui fait 6 x 6 = 36 cm².

4. Trouver la hauteur de la pyramide. Dans la plupart des cas, il sera indiqué sur l`image. Dans notre exemple, la hauteur de la pyramide est de 10 cm.

5. Multipliez l`aire de la base de la pyramide par la hauteur, et divisez par 3 pour trouver le volume. Rappelez-vous que la formule est V = 1/3 x b x h. Dans notre exemple, la pyramide a une base avec une aire de 36 et une hauteur de 10, donc le volume est de 36 x 10 x 1/3 = 120.

6. N`oubliez pas d`écrire le résultat en unités cubiques. Les mesures de la pyramide dans l`exemple ont été données en centimètres, le résultat doit donc être écrit en centimètres cubes, 120 cm³. Si les mesures ont été données en mètres, écrivez la réponse en mètres cubes (m³).
Méthode 5 sur 6: Calcul du volume d`un cône

1. Connaître les propriétés d`un cône. Un cône est une forme tridimensionnelle avec une base circulaire et un seul point sur la face opposée. Une autre façon de voir un cône est qu`il s`agit d`un type spécial de pyramide avec une base circulaire.
- Si la pointe du cône est directement au-dessus du centre de la base, cela s`appelle un cône droit. S`il n`est pas directement au-dessus du centre, on l`appelle un cône oblique. Heureusement, la formule pour calculer le volume est la même pour les deux types de cônes.

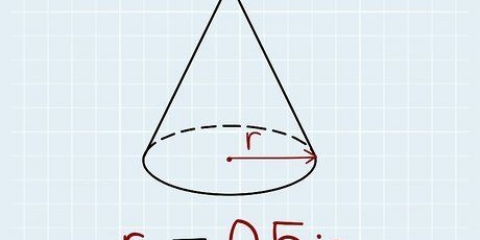
2. Connaître la formule pour calculer le volume du cône. Cette formule est V = 1/3 x π x r² x h, où r est le rayon du cercle à la base, h est la hauteur du cône et est la constante pi, qui peut être arrondie à 3,14.

3. Calculer l`aire de la base circulaire du cône. Pour ce faire, vous devez connaître le rayon de la base, qui doit être indiqué sur votre photo. Si vous avez le diamètre au lieu du rayon, divisez simplement ce nombre par 2, car le diamètre est 2 fois le rayon (d = 2 x r). Mettez ensuite le rayon dans la formule A = π x r² pour calculer l`aire.

4. Trouver la hauteur du cône. C`est la distance verticale de la base du cône au sommet. Dans notre exemple, la hauteur du cône est de 5 cm.

5. Multiplier la hauteur du cône par la surface de la base. Dans notre exemple, la surface de la base est de 28,27 cm² et la hauteur est de 5 cm, donc l x h = 28,27 x 5 = 141,35.

6. Multipliez maintenant ce résultat par 1/3 (ou divisez par 3) pour obtenir le volume du cône. Dans l`étape ci-dessus, nous avons en fait calculé le volume d`un cylindre, c`est-à-dire un cône où les parois seraient droites et se termineraient dans un autre cercle. Le diviser par 3 vous donne le volume du cône.

sept. N`oubliez pas d`écrire le résultat en unités cubiques. Notre cône a été mesuré en centimètres, donc le volume doit être exprimé en centimètres cubes : 47,12 cm³.
Méthode 6 sur 6: Calcul du volume d`une sphère

1. Reconnaître une sphère. Une sphère est une forme tridimensionnelle parfaitement ronde, dans laquelle chaque point de sa surface est à égale distance du centre. En d`autres termes, c`est une balle.

2. Apprendre la formule pour calculer le volume d`une sphère. La formule est V = 4/3 x π x r³ (c`est-à-dire : "quatre tiers pi fois r cube"), où r est le rayon de la sphère, et est la constante pi (3.14).

3. Trouver le rayon de la sphère. Si le rayon est déjà donné sur la photo, c`est facile. Étant donné le diamètre, divisez ce nombre par 2 pour obtenir le rayon. Le rayon de la sphère dans cet exemple est de 3 centimètres.

4. Mesurer la sphère si le rayon n`est pas donné. Si vous devez mesurer une sphère (comme une balle de tennis) pour trouver le rayon, trouvez une ficelle suffisamment longue pour l`enrouler tout autour. Ensuite, enroulez-le autour de l`objet au point le plus large et marquez le point où la ficelle rejoint. Mesurez ensuite cette partie de la ficelle avec une règle pour connaître la circonférence de la sphère. Divisez cela par 2 x , ou 6,28, alors vous connaissez le rayon.

5. Augmenter le rayon à la puissance 3 pour trouver r³. Élever à la troisième puissance signifie simplement multiplier le nombre trois fois par lui-même, donc r³ = r x r x r. Dans notre exemple r=3 qui devient 3 x 3 x 3 = 27.

6. Multipliez votre réponse par 4/3. Vous pouvez le faire avec une calculatrice, ou tout simplement le faire vous-même et simplifier la fraction. Dans notre exemple c`est 27 x 4/3 = 180/3, soit 36.

sept. Multipliez le résultat par pour trouver le volume de la sphère. La dernière étape du calcul du volume consiste à multiplier le résultat obtenu par π. Arrondissez π à deux décimales, c`est suffisant pour la plupart des problèmes de mathématiques (sauf si votre professeur dit le contraire), alors multipliez-le par 3,14 et vous avez votre réponse.

8. Écrivez votre réponse en unités cubes. Dans notre exemple, nous avons mesuré en centimètres, donc la réponse est V = 113,09 cm³.
Articles sur le sujet "Calculer le volume"
Оцените, пожалуйста статью
Populaire