Voir l`apothème comme le "x√3"-côté d`un triangle 30-60-90. Vous pouvez le voir comme ça parce que l`hexagone se compose de six triangles équilatéraux. L`apothème coupe l`un de ces triangles en deux, créant un triangle avec des angles de 30, 60 et 90 degrés. Vous savez que le côté opposé à l`angle de 60 degrés a une longueur de x√3, le côté opposé à l`angle de 30 degrés a une longueur de x, et le côté opposé à l`angle de 90 degrés a une longueur de 2x. Si 10√3 signifie "x√3," alors tu sais que x = 10. Vous savez que x est la moitié de la longueur du bas du triangle. Doublez ceci pour déterminer la longueur totale. Donc le bas du triangle est 20. Il y a six de ces côtés dans l`hexagone, donc pour trouver le périmètre de l`hexagone nous multiplions 20 par 6 = 120. 
Superficie = 1/2 x 120 x 10√3 Aire = 60 x 10√3 Superficie = 600√3 


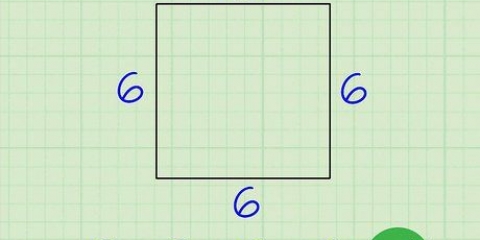
Si vous avez un carré avec des côtés de longueur 6, alors l`aire est 6 x 6 = 36. 
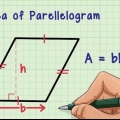
Si la base d`un rectangle est 4 et la hauteur est 3, alors l`aire est 4 x 3 = 12. 
Supposons que vous ayez un trapèze dont les bases ont des longueurs 6 et 8 et dont la hauteur est de 10. Alors l`aire est [(6 + 8) x 10]/2, qui peut être simplifiée en (14 x 10)/2 ou 140/2, qui est une aire de 70. 





Calculer l'aire d'un polygone
Teneur
Le calcul de l`aire d`un polygone peut être très simple lorsqu`il s`agit d`un triangle régulier. Mais cela devient beaucoup plus difficile lorsqu`il s`agit d`une forme irrégulière avec onze côtés. Si vous voulez savoir comment calculer l`aire de différents polygones, suivez ces étapes.
Pas
Partie 1 sur 3: Calcul de l`aire des polygones à l`aide de l`apothème

1. Écrivez la formule pour trouver l`aire d`un polygone régulier. Pour trouver l`aire d`un polygone régulier, il suffit de suivre la formule : aire = 1/2 x périmètre x apothème. Cela signifie ce qui suit :
- Circonférence = somme des longueurs de tous les côtés
- Apothème = le segment et aussi la distance du centre du polygone au centre d`un côté

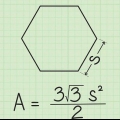
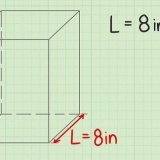
2. Déterminer l`apothème du polygone. Si vous utilisez la méthode de l`apothème, l`apothème sera toujours une donnée. Supposons que vous travaillez avec un hexagone dont l`apothème a une longueur de 10√3.

3. Déterminer le périmètre du polygone. Si la circonférence est une donnée, vous avez presque terminé. Mais probablement que l`apothème est une donnée. Si vous savez que c`est un polygone régulier, vous pouvez utiliser l`apothème pour déterminer son périmètre. C`est comme ça que tu fais ça :

4. Maintenant, nous pouvons mettre l`apothème et le périmètre dans la formule. Encore une fois: aire = 1/2 x périmètre x apothème, le périmètre est 120 et l`apothème est 10√3. Ensuite, la formule ressemble à ceci:

5. Simplifiez votre réponse. Peut-être devriez-vous écrire le résultat en décimales au lieu d`un radical. Utilisez votre calculatrice pour trouver la racine carrée approximative de trois et multipliez-la par 600. 3 x 600 = 1,039.2. C`est le résultat en décimales.
Partie 2 sur 3: Trouver l`aire d`un polygone régulier à l`aide d`autres formules

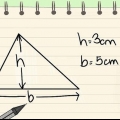
1. Calculer l`aire d`un triangle pair. Si vous voulez trouver l`aire d`un triangle régulier, vous pouvez utiliser cette formule : surface = 1/2 x base x hauteur.
- Si vous avez un triangle avec une base de 10 et une hauteur de 8, alors l`aire = 1/2 x 8 x 10 = 40.

2. Calculer l`aire d`un carré. Pour trouver l`aire d`un carré il suffit de multiplier un de ses côtés par lui-même, car la base et la hauteur sont égales pour un carré.

3. Calculer l`aire d`un rectangle. Pour trouver l`aire d`un rectangle il suffit de multiplier sa base par sa hauteur.

4.Calculer l`aire d`un trapèze. Pour trouver l`aire d`un trapèze, vous pouvez utiliser la formule suivante : aire = [(base 1 + base 2) x hauteur]/2.
Partie 3 sur 3: Trouver l`aire d`un polygone irrégulier

1. Utiliser les coordonnées des nœuds pour calculer l`aire. Si vous connaissez les coordonnées, vous pouvez calculer l`aire d`un polygone irrégulier.

2. Créer une séquence. Lister les coordonnées x et y de chaque sommet du polygone, dans le sens inverse des aiguilles d`une montre. Répétez les coordonnées du premier point en bas de la liste.

3. Multipliez la coordonnée x de chaque sommet par la coordonnée y du sommet suivant. Additionner les résultats. La somme de ces produits est 82.

4. Multipliez la coordonnée y de chaque sommet par la coordonnée x du sommet suivant. Additionner les résultats. La somme de ces produits est de -38.

5. Soustraire la somme des produits calculés à l`étape 4 de la somme des produits calculés à l`étape 3. (82) - (-38) = 120.

6. Divisez ce résultat par 2 pour trouver l`aire du polygone. Superficie = 120/2 = 60.
Des astuces
- Si vous listez les points dans le sens des aiguilles d`une montre au lieu de dans le sens inverse, vous obtenez également la zone, mais négative. Par exemple, vous pouvez l`utiliser comme un outil pour déterminer la séquence cyclique d`un ensemble de points qui forment un polygone.
- Cette formule calcule la surface avec l`orientation. Si vous l`utilisez sur une forme où deux des lignes se croisent comme dans un 8, vous obtenez la zone dans le sens inverse des aiguilles d`une montre moins la zone dans le sens des aiguilles d`une montre.
Articles sur le sujet "Calculer l'aire d'un polygone"
Оцените, пожалуйста статью
Populaire