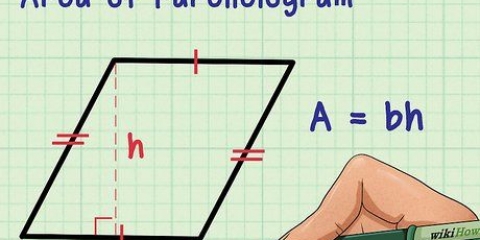Comment calculer l'aire d'un quadrilatère

Teneur

Donc pour tes devoirs tu dois calculer l`aire d`un quadrilatère...mais tu n`as même pas la moindre idée de ce qu`est un quadrilatère. Pas de panique, le sauvetage est proche! Un quadrilatère est une figure composée de 4 côtés/angles. Il suffit de déterminer le type de quadrilatère du problème et d`utiliser la formule correspondante pour calculer l`aire.

Pas

Méthode 1 sur 4: Carrés, rectangles et autres parallélogrammes

1. Apprenez à déterminer ce qu`est un parallélogramme. Un parallélogramme est un quadrilatère avec 2 paires de côtés parallèles, où les côtés parallèles sont de longueur égale. Carrés, rectangles et losanges sont tous des parallélogrammes.

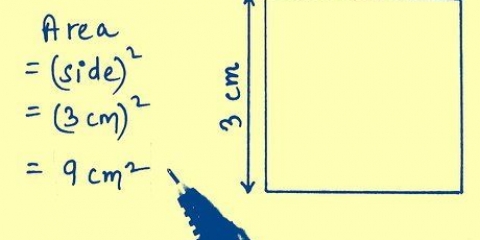
2. Trouver l`aire d`un carré. Étant donné que chaque côté d`un carré est de longueur égale, tout ce que vous avez à faire est de mesurer la longueur d`un côté (appelez-le "t"), pour trouver l`aire d`un carré. Cela revient à multiplier la base du carré par sa hauteur ; la base et la hauteur sont toujours les mêmes. Utilisez la formule suivante :

K = t

C`est la même chose que K = t * t

Si un côté d`un carré a une longueur de 4, (t = 4), alors l`aire est t, ou 4 x 4 = 16.

3. Trouver l`aire d`un rectangle. Pour trouver l`aire d`un rectangle il faut connaître la longueur et la largeur du rectangle. La formule est la suivante :

K = b*h

Si la longueur est de longueur 10 et la largeur de 5, alors l`aire du rectangle est de 10 x 5 (l * w) = 50.

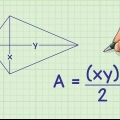
4. Trouver l`aire d`un carré. Cela peut être délicat - vous ne pouvez pas simplement multiplier un côté par l`autre ici. Vous devrez maintenant tracer des lignes à partir de chaque point et mesurer les diagonales de la forme, si elles ne sont pas données. Multipliez ensuite les diagonales comme ceci :

K = (b*h)/2, pour laquelle b = diagonale 1 et h = diagonale 2

Si un carré a des diagonales de longueur 6 puis 8, alors l`aire est (6 x 8)/2 = 48/2 = 24

Méthode 2 sur 4: L`aire d`un trapèze

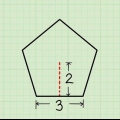
1. Déterminer s`il s`agit d`un trapèze. Un trapèze est un quadrilatère dont au moins 2 côtés sont parallèles. Chacun des quatre côtés d`un trapèze peut avoir une longueur différente. Il existe deux manières différentes de trouver l`aire d`un trapèze, en fonction des informations données.

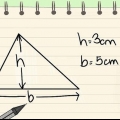
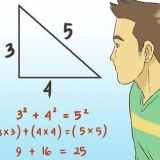
2. Déterminer la hauteur du trapèze. La hauteur d`un trapèze est la ligne perpendiculaire reliant la ligne de base supérieure et la ligne de base inférieure, et vous avez besoin des deux pour calculer l`aire. C`est ne pas de la même longueur que l`un des côtés, car chaque côté est diagonal. Voici comment trouver la hauteur :

Déterminer quelle est la base la plus courte. Placez votre crayon dans le coin entre la ligne de base et tracez une ligne droite vers le haut ou vers le bas jusqu`à l`autre ligne de base. Vous devriez maintenant avoir dessiné un triangle avec un angle de 90 degrés.

Utiliser la trigonométrie pour déterminer la hauteur. Par exemple, si vous connaissez la longueur d`un côté et que l`angle adjacent est connu, et qu`il y a un angle de 90 degrés dans le triangle, alors la hauteur est la longueur du côté multipliée par le sinus de l`angle.

Supposons que la hauteur du trapèze est de 10.

3. Déterminer l`aire du trapèze en utilisant la hauteur et la longueur de la base. Si vous connaissez la hauteur du trapèze et la longueur des deux côtés de la base, utilisez la formule suivante :

K = (a+b)/2 * h

Si la hauteur est de 10 et que la base a une longueur de 7 et 9, alors vous pouvez trouver l`aire en calculant : (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80

4. Trouver l`aire d`un trapèze en utilisant le segment médian. Ce segment médian est une ligne parallèle aux lignes inférieure et supérieure du trapèze, et a une longueur exactement entre les deux. Voici comment vous travaillez :

Déterminer le segment médian. Pour déterminer la longueur du segment médian m, on prend la moyenne des longueurs des côtés une et b (ou la ligne inférieure et supérieure du trapèze).Utilisez la formule : m = (a+b)/2.Maintenant que vous connaissez la longueur du segment médian, vous pouvez la multiplier par la hauteur pour trouver la zone. Utilisez la formule suivante :

K = m*h

C`est essentiellement la même formule que l`original, mais remplace maintenant "m" le terme (a + b)/2.

Supposons que vous connaissiez le segment médian de ce trapèze. Supposons que ce soit 8, alors l`aire du trapèze est de 8 x 10 = 80, tout comme avec la méthode précédente.

Méthode 3 sur 4: Détermination de la surface d`un cerf-volant

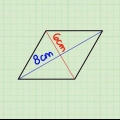
1. Qu`est-ce qu`un cerf-volant. Un cerf-volant est défini comme une forme géométrique où 2 paires de côtés de longueur égale sont connectés ensemble, ce qui ressemble à un cerf-volant régulier. Il existe deux manières différentes de trouver l`aire de cette figure, en fonction des informations données.

2. Trouver l`aire d`un cerf-volant en utilisant la longueur de ses côtés. Si vous connaissez la longueur de deux côtés différents d`un cerf-volant et que vous connaissez l`angle entre ces côtés, utilisez la formule suivante où l`angle est égal à thêta (θ) :

K =(a*b) * sin

3. Trouver l`aire d`un cerf-volant à l`aide des diagonales. Une diagonale est la ligne droite entre deux coins opposés du cerf-volant. Chaque cerf-volant a 2 diagonales.

Déterminer la longueur de chaque diagonale. Tracez une ligne d`un coin d`un cerf-volant à l`opposé. Vous devriez maintenant avoir 2 triangles. Déterminer en utilisant Cet article, quelle est la longueur de la diagonale (les trois angles d`un triangle font 180 degrés).

Une fois que vous avez déterminé la première diagonale, utilisez les mêmes principes pour déterminer la longueur de l`autre. Ensuite, utilisez cette formule pour déterminer la zone, où p et q représentent la longueur des diagonales :

K = (p*q)/2

Si les diagonales ont des longueurs 4 et 6, alors vous pouvez trouver l`aire du cerf-volant comme suit : (4 x 6)/2 = 24/2 = 12

Notez que cette formule fonctionne également pour la zone d`un losange, car il s`agit d`un type spécial de cerf-volant, où tous les côtés ont la même longueur.

Méthode 4 sur 4: Une formule générale

1. La formule générale pour déterminer l`aire d`un quadrilatère. Il existe des formules pour déterminer l`aire de n`importe quel quadrilatère, quelle que soit sa forme. Voici la forme la plus générale, utilisant les principes trigonométriques :

si k est l`aire totale du quadrilatère, une, b, c et ré représentent les longueurs des 4 côtés, une est l`angle (en degrés) entre les côtés une et ré et C est l`angle (en degrés) entre les côtés b et c, puis:
K = 0.5*a*d * sin A + 0.5*b*c * péché C
Si vous essayez de trouver l`aire d`un parallélogramme où les angles opposés sont égaux, la formule devient plus simple : K = 0.5*(ad + bc) * sin A.