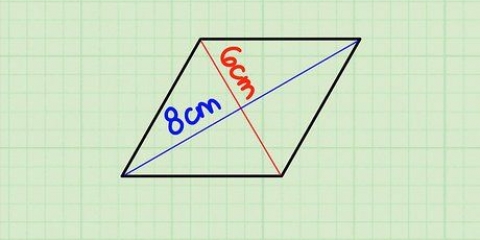
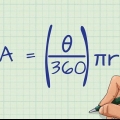Par exemple, si un cerf-volant a deux diagonales de 7 cm et 10 cm, votre formule ressemblerait à ceci : .
. 
Par exemple:



Par exemple:


L`aire d`un cerf-volant avec des diagonales de 10 cm et 7 cm est donc de 35 cm carré. 

Par exemple, si votre cerf-volant a un côté de 20 cm et un côté de 15 cm, votre formule ressemblera à ceci :  .
. 
Par exemple:



Par exemple : si l`angle  alors votre formule ressemblera à ceci:
alors votre formule ressemblera à ceci:  .
. 
Par exemple, le sinus d`un angle de 150 degrés est de 0,5, donc votre formule ressemblera à ceci :  .
. 
Par exemple:


Ainsi la surface d`un cerf-volant, avec deux côtés de 20 cm et 15 cm, et l`angle entre eux de 150 degrés, est de 150 cm carré. 

Par exemple, si votre cerf-volant a une superficie de 35 cm carrés, votre formule ressemblera à ceci :  .
. 
Par exemple, si vous savez qu`une des diagonales mesure 7 cm de long, votre formule ressemblera à ceci :  .
. 
Par exemple:




Par exemple:



La longueur de la diagonale manquante d`un cerf-volant, étant donné une aire de 35 cm carrés et une diagonale de 7 cm, est donc de 10 cm.
Calculer l'aire d'un cerf-volant
Teneur
Un cerf-volant est un type de quadrilatère avec deux paires de côtés égaux et adjacents. Les cerfs-volants peuvent avoir l`apparence traditionnelle d`un cerf-volant, mais un cerf-volant peut aussi être un losange ou un carré. Peu importe à quoi ressemble un cerf-volant, les méthodes pour trouver la surface seront les mêmes. Si vous connaissez la longueur des diagonales, vous pouvez trouver l`aire grâce à des calculs simples. Vous pouvez également utiliser la trigonométrie pour trouver la zone, si vous connaissez les côtés et les angles de la figure.
Pas
Méthode 1 sur 3 : Utiliser les diagonales pour déterminer l`aire

1. Écrivez la formule de l`aire d`un cerf-volant, étant donné deux diagonales. La formule est  , par lequel
, par lequel  est égal à la surface du cerf-volant, et
est égal à la surface du cerf-volant, et  et
et  est égal à la longueur des diagonales du cerf-volant.
est égal à la longueur des diagonales du cerf-volant.
 , par lequel
, par lequel  est égal à la surface du cerf-volant, et
est égal à la surface du cerf-volant, et  et
et  est égal à la longueur des diagonales du cerf-volant.
est égal à la longueur des diagonales du cerf-volant.
2. Appliquer les longueurs des diagonales à la formule. Une diagonale est une ligne droite qui va d`un sommet au sommet de l`autre côté. Vous devez soit obtenir la longueur des diagonales, soit être capable de les mesurer. Si vous ne connaissez pas la longueur des diagonales, vous ne pouvez pas utiliser cette méthode.
 .
.
3. Multiplier les longueurs des diagonales. Le produit devient le nouveau compteur dans la comparaison de zone.



4. Divisez le produit des diagonales par 2. Cela vous donnera la surface du cerf-volant, en unités carrées.


L`aire d`un cerf-volant avec des diagonales de 10 cm et 7 cm est donc de 35 cm carré.
Méthode 2 sur 3: Utiliser un angle et deux côtés pour déterminer la zone

1. Écris la formule de la surface du cerf-volant. Cette formule fonctionne si vous connaissez deux côtés non conformes et la taille de l`angle entre ces deux côtés. La formule est  , par lequel
, par lequel  est égal à la surface du cerf-volant,
est égal à la surface du cerf-volant,  et
et  est égal aux côtés inégaux du cerf-volant, et
est égal aux côtés inégaux du cerf-volant, et  est égal à l`angle entre les côtés
est égal à l`angle entre les côtés et
et  .
.
 , par lequel
, par lequel  est égal à la surface du cerf-volant,
est égal à la surface du cerf-volant,  et
et  est égal aux côtés inégaux du cerf-volant, et
est égal aux côtés inégaux du cerf-volant, et  est égal à l`angle entre les côtés
est égal à l`angle entre les côtés et
et  .
. - Vérifiez si vous avez deux côtés inégaux. Un cerf-volant a deux paires de côtés congrus. Vous devez utiliser un côté de chaque paire. Assurez-vous de commencer à partir de l`angle entre ces deux côtés. Si vous n`avez pas toutes ces informations, vous ne pouvez pas utiliser cette méthode.

2. Appliquer la longueur des côtés à la formule. Cette information doit être donnée, sinon vous devez pouvoir la mesurer. N`oubliez pas que vous utilisez des côtés non congrus, donc chaque côté a une longueur différente.
 .
.
3. Multipliez les côtés entre eux. Appliquer ce produit à la formule.



4. Appliquer l`angle à la formule. Assurez-vous d`utiliser l`angle entre les deux côtés non congruents.
 alors votre formule ressemblera à ceci:
alors votre formule ressemblera à ceci:  .
.
5. Déterminer le sinus de l`angle. Pour cela, vous pouvez utiliser une calculatrice, ou une table trigonométrique.
 .
.
6. Multiplier le produit des côtés par le sinus de l`angle. Ce résultat est l`aire du cerf-volant, en unités carrées.


Ainsi la surface d`un cerf-volant, avec deux côtés de 20 cm et 15 cm, et l`angle entre eux de 150 degrés, est de 150 cm carré.
Méthode 3 sur 3: Utiliser la zone pour trouver une diagonale manquante

1. Écrivez la formule de l`aire d`un cerf-volant, étant donné deux diagonales. La formule est  , par lequel
, par lequel  est égal à la surface du cerf-volant, et
est égal à la surface du cerf-volant, et  et
et  est égal à la longueur des diagonales du cerf-volant.
est égal à la longueur des diagonales du cerf-volant.
 , par lequel
, par lequel  est égal à la surface du cerf-volant, et
est égal à la surface du cerf-volant, et  et
et  est égal à la longueur des diagonales du cerf-volant.
est égal à la longueur des diagonales du cerf-volant.
2. Appliquer la zone du cerf-volant à la formule. Cette information doit être donnée. Assurez-vous  remplace.
remplace.
 remplace.
remplace. .
.
3. appliquer la longueur de la diagonale connue à la formule. remplacer  .
.
 .
. .
.
4. Multiplier chaque côté de l`équation par 2. Cela supprimera la fraction dans la formule.




5. Divisez chaque côté de l`équation par la longueur de la diagonale. Cela vous donnera la longueur de la diagonale manquante.



La longueur de la diagonale manquante d`un cerf-volant, étant donné une aire de 35 cm carrés et une diagonale de 7 cm, est donc de 10 cm.
Nécessités
- Calculatrice (facultatif)
- Règle (facultatif)
- Crayon (facultatif)
- Papier (facultatif)
Articles sur le sujet "Calculer l'aire d'un cerf-volant"
Оцените, пожалуйста статью
Similaire
Populaire