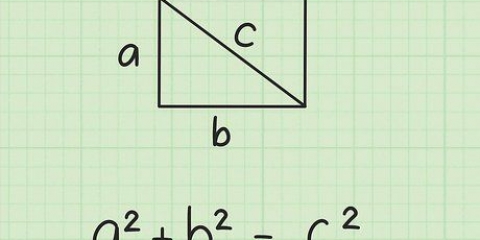
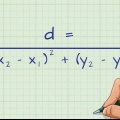Les deux côtés les plus courts du triangle sont les côtés du carré : chacun a une longueur s. L`hypoténuse est la diagonale du carré, ré. 


Simplifier: 
Divisez les deux côtés par deux : 
Superficie = 
Superficie = 

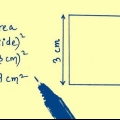
Par exemple, supposons qu`un carré a une diagonale de 10 cm. Superficie = 
=
= 50cm. Par exemple, un carré avec une diagonale de 10 cm a des côtés de longueur  cm.
cm. Si vous voulez trouver à la fois la longueur d`un côté et l`aire de la diagonale, vous pouvez d`abord utiliser cette formule puis carré la réponse pour l`aire : Aire  cm. C`est un peu moins précis, car
cm. C`est un peu moins précis, car  est un nombre irrationnel qui peut avoir des erreurs d`arrondi.
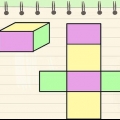
est un nombre irrationnel qui peut avoir des erreurs d`arrondi. Dessiner un carré sur papier. Assurez-vous que tous les côtés sont égaux. Mesurer la diagonale. Dessinez un deuxième carré avec cette longueur comme côtés du carré. Trace une copie de ton premier carré pour en avoir deux. Découpez les trois carrés. Coupez les deux petits carrés en formes qui s`adaptent à l`intérieur du grand carré. Ils doivent remplir parfaitement l`espace, pour montrer que l`aire du grand carré est exactement le double de l`aire du plus petit carré.
Calcul de l'aire d'un carré à l'aide de la diagonale
Teneur
La formule la plus courante pour l`aire d`un carré est simple : c`est la longueur d`un de ses côtés au carré, ou s. Mais parfois, vous ne connaissez que la longueur de la diagonale d`un carré, la ligne entre deux sommets opposés. Si vous êtes familier avec les triangles rectangles, vous pouvez dériver une nouvelle formule avec la diagonale comme seule variable.
Pas
Partie 1 sur 2: Calculer l`aire d`un carré

1. Dessine ton carré. Un carré a quatre côtés égaux. Disons que chaque côté a une longueur de `s`.

2. Utiliser la formule standard pour l`aire d`un carré. L`aire d`un carré est égale à sa longueur multipliée par sa largeur. Parce que chaque côté s est devient formule Aire = s x s = s. Cela s`avérera utile bientôt.

3. Reliez deux coins opposés pour faire une diagonale. La mesure de cette diagonale devient ré unités. Cette diagonale divise le carré en deux triangles rectangles.

4.Utiliser le théorème de Pythagore pour l`un des triangles. Le théorème de Pythagore est une formule pour trouver l`hypoténuse (côté le plus long) d`un triangle rectangle : (côté A) + (côté B) = (hypoténuse) ou  . Maintenant que le carré a été divisé en deux, vous pouvez utiliser cette formule sur l`un des triangles rectangles :
. Maintenant que le carré a été divisé en deux, vous pouvez utiliser cette formule sur l`un des triangles rectangles :
 . Maintenant que le carré a été divisé en deux, vous pouvez utiliser cette formule sur l`un des triangles rectangles :
. Maintenant que le carré a été divisé en deux, vous pouvez utiliser cette formule sur l`un des triangles rectangles :

5. Arranger l`équation de sorte que s soit d`un côté. N`oubliez pas que nous savons que l`aire du carré est s. Si vous pouvez isoler s d`un côté, vous avez une nouvelle équation pour l`aire :






6. Utilisez cette formule avec un exemple de carré. Ces étapes ont prouvé que la formule Aire =  s`applique à tous les carrés. Entrez la longueur de la diagonale pour ré et résoudre.
s`applique à tous les carrés. Entrez la longueur de la diagonale pour ré et résoudre.
 s`applique à tous les carrés. Entrez la longueur de la diagonale pour ré et résoudre.
s`applique à tous les carrés. Entrez la longueur de la diagonale pour ré et résoudre.
=

= 50cm.
Partie 2 sur 2: Informations supplémentaires
1. Trouver la diagonale de la longueur d`un côté. Le théorème de Pythagore pour un carré de côté s et diagonale ré donne la formule  au. Résolvez pour « d » si vous connaissez les longueurs des côtés et souhaitez déterminer la longueur de la diagonale :
au. Résolvez pour « d » si vous connaissez les longueurs des côtés et souhaitez déterminer la longueur de la diagonale :
 au. Résolvez pour « d » si vous connaissez les longueurs des côtés et souhaitez déterminer la longueur de la diagonale :
au. Résolvez pour « d » si vous connaissez les longueurs des côtés et souhaitez déterminer la longueur de la diagonale : - Par exemple, si un carré a 7 cm de côté, alors la diagonale est d = 7√2 cm, soit environ 9,9 cm.
- Si vous n`avez pas de calculatrice, vous pouvez utiliser 1,4 comme estimation de √2.
2. Déterminer la longueur d`un côté à l`aide de la diagonale. La diagonale est-elle donnée et vous savez que la diagonale d`un carré  alors vous pouvez diviser les deux côtés par
alors vous pouvez diviser les deux côtés par  à
à  pour obtenir.
pour obtenir.
 alors vous pouvez diviser les deux côtés par
alors vous pouvez diviser les deux côtés par  à
à  pour obtenir.
pour obtenir. cm.
cm. cm. C`est un peu moins précis, car
cm. C`est un peu moins précis, car  est un nombre irrationnel qui peut avoir des erreurs d`arrondi.
est un nombre irrationnel qui peut avoir des erreurs d`arrondi.3. Interpréter la formule de surface. La formule Aire =  semble être mathématiquement correct, mais existe-t-il un moyen de tester cela directement? Bien,
semble être mathématiquement correct, mais existe-t-il un moyen de tester cela directement? Bien,  est l`aire d`un deuxième carré avec la diagonale comme côté. Parce que la formule complète
est l`aire d`un deuxième carré avec la diagonale comme côté. Parce que la formule complète  vous pouvez raisonner que ce deuxième carré a exactement le double de l`aire du carré d`origine. Vous pouvez tester cela vous-même :
vous pouvez raisonner que ce deuxième carré a exactement le double de l`aire du carré d`origine. Vous pouvez tester cela vous-même :
 semble être mathématiquement correct, mais existe-t-il un moyen de tester cela directement? Bien,
semble être mathématiquement correct, mais existe-t-il un moyen de tester cela directement? Bien,  est l`aire d`un deuxième carré avec la diagonale comme côté. Parce que la formule complète
est l`aire d`un deuxième carré avec la diagonale comme côté. Parce que la formule complète  vous pouvez raisonner que ce deuxième carré a exactement le double de l`aire du carré d`origine. Vous pouvez tester cela vous-même :
vous pouvez raisonner que ce deuxième carré a exactement le double de l`aire du carré d`origine. Vous pouvez tester cela vous-même :Des astuces
- Cette équation simple est utilisée dans de nombreux domaines, notamment la cristallographie, la chimie et l`art. Par exemple, vous pouvez l`utiliser pour calculer la superficie d`un paysage que vous voyez lors d`un arpentage, ou lorsque vous utilisez la perspective en photographie ou en peinture, en mesurant la distance que vous avez parcourue et en imaginant une grille de cette distance comme la diagonale.
- Si vous souhaitez adopter une approche plus visuelle des mathématiques, ou apprendre à utiliser des graphiques et des tableaux dans l`art, ou explorer le chemin en spirale d`une particule, consultez quelques articles sur Microsoft Excel, les mathématiques, les feuilles de calcul et les graphiques.
- Si vous n`avez pas de calculatrice mais que vous avez besoin d`une estimation plus précise de la racine carrée de deux, il existe des moyens de faire ça à la main. Un exemple de ceci est la méthode de Newton-Raphson.
Articles sur le sujet "Calcul de l'aire d'un carré à l'aide de la diagonale"
Оцените, пожалуйста статью
Similaire
Populaire