Comment calculer la longueur de la diagonale dans un rectangle

Teneur

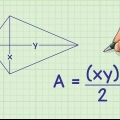
Une diagonale est une ligne droite reliant un coin d`un rectangle au coin opposé. Un rectangle a deux diagonales de même longueur. Si vous connaissez les longueurs des côtés d`un rectangle, il est facile de trouver la longueur de la diagonale en utilisant le théorème de Pythagore, car une diagonale divise un rectangle en deux triangles rectangles. Si vous ne connaissez pas les longueurs des côtés, mais que vous disposez d`autres données (telles que l`aire et le périmètre, ou le rapport entre les longueurs des côtés), vous pouvez mesurer la longueur et la largeur des côtés avec un quelques étapes supplémentaires. Trouvez le rectangle, puis en utilisant le théorème de Pythagore, trouvez la longueur et la largeur de la diagonale.

Pas

Méthode 1 sur 3: Utilisation de la longueur et de la largeur

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 1

1. Écrire la formule du théorème de Pythagore. La formule est

une 2 + b^{2} = c^{2}

$a^{{2}}+b^{{2}}=c^{{2}}$ , par lequel

une

$une$ et

b

$b$ sont égales aux longueurs des côtés d`un triangle rectangle, et

c

$c$ est égal à la longueur de l`hypoténuse d`un triangle rectangle.

Vous utilisez le théorème de Pythagore car la diagonale d`un rectangle le divise en deux triangles rectangles congrus. La longueur et la largeur du rectangle sont les longueurs des côtés du triangle ; la diagonale est l`hypoténuse du triangle.

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 2

2. Appliquer la longueur et la largeur à la formule. Ce sont s`il est donné correctement, ou vous pouvez les mesurer. Assurez-vous de remplacer

une

$une$ et

b

$b$ .

Par exemple, si la largeur d`un rectangle est de 3 cm et sa longueur de 4 cm, votre formule ressemblera à ceci :

32 + 4^{2} = c^{2}

$3^{{2}}+4^{{2}}=c^{{2}}$ .

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 3

3. Carré la longueur et la largeur, puis additionner ces nombres ensemble. La quadrature multiplie le nombre par lui-même.

Par exemple:

32 + 4^{2} = c^{2}

$3^{{2}}+4^{{2}}=c^{{2}}$

9 + 16 = c 2

$9+16=c^{{2}}$

25 = c 2

$25=c^{{2}}$

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 4

4. Soustraire la racine carrée de chaque côté de l`équation. La façon la plus simple de trouver une racine carrée est d`utiliser une calculatrice. Vous pouvez utiliser une calculatrice en ligne si vous n`avez pas de calculatrice scientifique. Cela vous donne la valeur

c

$c$ , ou l`hypoténuse du triangle et la diagonale du rectangle.

Par exemple:

25 = c 2

$25=c^{{2}}$

\sqrt{25} = \sqrt{c} 2

${sqrt{25}}={sqrt{c^{{2}}}}$

5 = c

$5=c$
Ainsi, la diagonale ou le rectangle d`une largeur de 3 cm et d`une longueur de 4 cm vaut 5 cm.

Méthode 2 sur 3: Utilisation de la zone et du périmètre

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 5

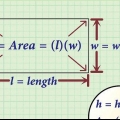
1. Ecrire la formule de l`aire d`un rectangle. La formule est

une = je w

$A=lw$ , par lequel

une

$une$ est égal à l`aire du rectangle,

je

$je$ est égal à la longueur du rectangle, et

w

$w$ est égal à la largeur du rectangle.

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 6

2. Utiliser l`aire du rectangle dans la formule. Assurez-vous de remplacer la bonne variable

une

$une$ .

Par exemple, si l`aire du rectangle est de 35 centimètres carrés, votre formule ressemblerait à ceci :

35 = je w

$35=lw$ .

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 7

3. Réorganisez la formule et vous obtenez une valeur pour w{style d`affichage w} $w$ . Pour ce faire, divisez les deux côtés de l`équation par

je

$je$ . Mettez cette valeur de côté. Vous l`utiliserez plus tard dans la formule du périmètre.

Par exemple:

35 = je w

$35=lw$

\frac{35}{je} = w

${frac{35}{l}}=w$ .

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 8

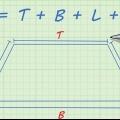
4. Écrire la formule du périmètre d`un rectangle. La formule est

p = 2 (w + je)

$P=2(w+1)$ , par lequel

w

$w$ est égal à la largeur du rectangle, et

je

$je$ est égal à la longueur du rectangle.

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 9

5. Utiliser la valeur du périmètre dans la formule. Assurez-vous de remplacer la variable

p

$p$ .

Par exemple, si le périmètre d`un rectangle est de 24 centimètres, votre formule ressemblera à ceci :

24 = 2 (w + je)

$24=2(w+l)$ .

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 10

6. Divisez les deux côtés de l`équation par 2. Cela vous donne la valeur

w + je

$w+l$ .

Par exemple:

24 = 2 (w + je)

$24=2(w+l)$

\frac{24}{2} = 2 (w + je) 2

${frac{24}{2}}={frac{2(w+l)}{2}}$

12 = w + je

$12=w+l$ .

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 11

sept. Utiliser la valeur w{style d`affichage w} $w$ dans l`équation. Utilisez la valeur que vous avez trouvée en réorganisant la formule de la zone.

Par exemple, si vous trouvez avec la formule de surface que

\frac{35}{je} = w

${frac{35}{l}}=w$ , alors tu remplaces la valeur

w

$w$ dans la formule circonférentielle :

12 = w + je

$12=w+l$

12 = \frac{35}{je} + je

$12={frac{35}{l}}+l$

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 12

8. Éliminer la fraction dans l`équation. Pour ce faire, multipliez les deux côtés de l`équation par

je

$je$ .

Par exemple:

12 = \frac{35}{je} + je

$12={frac{35}{l}}+l$

12 \times je = (\frac{35}{je} \times je) + (je \times je)

$12fois l=({frac{35}{l}}fois l)+(lfois l)$

12 je = 35 + je 2

$ch12=35+ch^{{2}}$

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 13

9. Mettre l`équation égale à 0. Pour ce faire, soustrayez le terme du premier degré des deux côtés de l`équation.

Par exemple:

12 je = 35 + je 2

$ch12=35+ch^{{2}}$

12 je - 12 je = 35 + je 2 - 12 je

$ch12-12ch=35+ch^{{2}}-12ch$

0 = 35 + je 2 - 12 je

$0=35+ch^{{2}}-12ch$

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 14

dix. Réorganiser l`ordre des termes dans l`équation. Cela signifie que le terme avec l`exposant vient en premier, suivi du terme avec la variable, et enfin de la constante. Lors de la réorganisation, faites attention aux bons signes positifs et négatifs. L`équation est maintenant ordonnée comme une équation quadratique.

Par exemple,

0 = 35 + je 2 - 12 je

$0=35+ch^{{2}}-12ch$ devient

0 = je 2 - 12 je + 35

$0=ch^{{2}}-12ch+35$ .

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 15

11. Factoriser l`équation quadratique. Pour obtenir des instructions détaillées sur la façon de procéder, lisez l`article Résoudre des équations quadratiques.

Par exemple, l`équation

0 = je 2 - 12 je + 35

$0=ch^{{2}}-12ch+35$ peut être dissous dans

0 = (je - sept) (je - 5)

$0=(l-7)(l-5)$ .

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 16

12. Déterminer les valeurs de je{style d`affichage l} $je$ . Pour ce faire, définissez chaque terme sur zéro et résolvez la variable. Vous obtenez deux solutions à cette équation. Puisque vous avez affaire à un rectangle, les deux solutions seront la largeur et la longueur de votre rectangle.

Par exemple:

0 = (je - sept)

$0=(l-7)$

sept = je

$7=l$
ET

0 = (je - 5)

$0=(l-5)$

5 = je

$5=l$ .
Ainsi, la longueur et la largeur du rectangle sont de 7 cm et 5 cm.

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 17

13. Écrire la formule du théorème de Pythagore. La formule est

une 2 + b^{2} = c^{2}

$a^{{2}}+b^{{2}}=c^{{2}}$ , par lequel

une

$une$ et

b

$b$ sont égales aux longueurs des côtés d`un triangle rectangle, et

c

$c$ est égal à la longueur de l`hypoténuse d`un triangle rectangle.

Vous utilisez le théorème de Pythagore car la diagonale d`un rectangle le divise en deux triangles rectangles congrus. La largeur et la longueur du rectangle sont les longueurs des côtés du triangle ; la diagonale est l`hypoténuse du triangle.

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 18

14. Utilisez la latitude et la longitude dans la formule. Peu importe la valeur que vous utilisez pour quelle variable.

Par exemple, si vous savez que la largeur et la longueur du rectangle sont de 5 cm et 7 cm, votre formule ressemblera à ceci :

52 + {sept}^{2} = c^{2}

$5^{{2}}+7^{{2}}=c^{{2}}$ .

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 19

15. Mettez la latitude et la longitude au carré, puis additionnez ces nombres. Carré signifie multiplier un nombre par lui-même.

Par exemple:

52 + {sept}^{2} = c^{2}

$5^{{2}}+7^{{2}}=c^{{2}}$

25 + 49 = c 2

$25+49=c^{{2}}$

74 = c 2

$74=c^{{2}}$

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 20

16. Prendre la racine carrée de chaque côté de l`équation. La façon la plus simple de trouver une racine carrée est d`utiliser une calculatrice. Vous pouvez utiliser une calculatrice en ligne si vous n`avez pas de calculatrice scientifique. Cela vous donne la valeur

c

$c$ , et c`est l`hypoténuse du triangle, et la diagonale du rectangle.

Par exemple:

74 = c 2

$74=c^{{2}}$

\sqrt{74} = \sqrt{c} 2

${sqrt{74}}={sqrt{c^{{2}}}}$

8.6024 = c

$8.6024=c$
Donc la diagonale d`un rectangle d`une aire de 35 cm et d`un périmètre de 24 cm est d`environ 8,6 cm.

Méthode 3 sur 3: Utilisation de l`aire et des longueurs relationnelles des côtés

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 21

1. Écrivez une formule qui explique la relation entre les longueurs des côtés. Vous pouvez modifier la longueur (

je

$je$ ) ou la largeur (

w

$w$ ) isoler. Mettez cette formule de côté un instant. Vous l`utiliserez bientôt dans la formule de surface.

Par exemple, si vous savez que la largeur d`un rectangle est supérieure de 2 cm à sa longueur, vous pouvez écrire une formule comme $w$ $w$ : $w = je + 2$ $w=l+2$ .

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 22

2. Ecrire la formule de l`aire d`un rectangle. La formule est

une = je w

$A=lw$ , par lequel

une

$une$ est égal à l`aire du rectangle,

je

$je$ est égal à la longueur du rectangle, et

w

$w$ est égal à la largeur du rectangle.

Vous pouvez utiliser cette méthode si vous connaissez le périmètre du rectangle, sauf que vous utilisez maintenant la formule du périmètre au lieu de la formule de l`aire. La formule du périmètre d`un rectangle est

p = 2 (w + je)

$P=2(w+1)$ , par lequel

w

$w$ est égal à la largeur du rectangle, et

je

$je$ est égal à la longueur du rectangle.

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 23

3. Utiliser l`aire du rectangle dans la formule. Assurez-vous de remplacer la variable

une

$une$ .

Par exemple, si l`aire du rectangle est de 35 centimètres carrés, votre formule ressemblerait à des volts :

35 = je w

$35=lw$ .

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 24

4. Utilisez la formule relationnelle pour la longueur (ou la largeur) dans la formule. Puisque vous avez affaire à un rectangle, peu importe si vous travaillez avec une variable

je

$je$ ou

w

$w$ .

Par exemple, si vous avez trouvé que

w = je + 2

$w=l+2$ , alors vous substituez cette relation à

w

$w$ dans la formule de surface :

35 = je w

$35=lw$

35 = je (je + 2)

$35=l(l+2)$

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 25

5. Faites-en une équation quadratique. Pour ce faire, utilisez la propriété distributive et multipliez les termes entre parenthèses ensemble, après quoi vous définissez l`équation égale à 0.

Par exemple:

35 = je (je + 2)

$35=l(l+2)$

35 = je 2 + 2 je

$35=ch^{{2}}+ch2$

0 = je 2 + 2 je - 35

$0=ch^{{2}}+ch2-35$

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 26

6. Factoriser l`équation quadratique. Pour obtenir des instructions détaillées sur la façon de procéder, lisez l`article Résoudre des équations quadratiques.

Par exemple, l`équation

0 = je 2 + 2 je - 35

$0=ch^{{2}}+ch2-35$ peut être dissous comme

0 = (je + sept) (je - 5)

$0=(l+7)(l-5)$ .

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 27

sept. Déterminer les valeurs de je{style d`affichage l} $je$ . Pour ce faire, rendez chaque terme égal à zéro et résolvez la variable. Tu trouves deux solutions à l`équation.

Par exemple:

0 = (je + sept)

$0=(l+7)$

- sept = je

$-7=ch$
ET

0 = (je - 5)

$0=(l-5)$

5 = je

$5=l$ .
Dans ce cas, il y a une réponse négative. Puisque la longueur d`un rectangle ne peut pas être négative, vous savez que la longueur doit être de 5 cm.

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 28

8. Utilisez la valeur de la longueur (ou largeur) dans votre formule de relation. Cela vous donnera la longueur de l`autre côté du rectangle.

Par exemple, si vous savez que la longueur du rectangle est de 5 cm, et que le rapport entre les longueurs des côtés est

w = je + 2

$w=l+2$ , alors vous entrez 5 comme longueur dans la formule :

w = je + 2

$w=l+2$

w = 5 + 2

$w=5+2$

w = sept

$w=7$

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 29

9. Écrire la formule du théorème de Pythagore. La formule est

une 2 + b^{2} = c^{2}

$a^{{2}}+b^{{2}}=c^{{2}}$ , par lequel

une

$une$ et

b

$b$ sont égales aux longueurs des côtés d`un triangle rectangle, et

c

$c$ est égal à la longueur de l`hypoténuse d`un triangle rectangle.

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 30

dix. Utilisez la latitude et la longitude dans la formule. Peu importe la valeur que vous utilisez pour quelle variable.

Par exemple, si vous savez que la largeur et la longueur du rectangle sont égales à 5 cm et 7 cm, votre formule ressemble maintenant à ceci :

52 + {sept}^{2} = c^{2}

$5^{{2}}+7^{{2}}=c^{{2}}$ .

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 31

11. Mettez la latitude et la longitude au carré, puis additionnez ces nombres. Carré signifie multiplier un nombre par lui-même.

Par exemple:

52 + {sept}^{2} = c^{2}

$5^{{2}}+7^{{2}}=c^{{2}}$

25 + 49 = c 2

$25+49=c^{{2}}$

74 = c 2

$74=c^{{2}}$

Image intitulée Trouver la mesure de la diagonale à l`intérieur d`un rectangle Étape 32

12. Soustraire la racine carrée de chaque côté de l`équation. La façon la plus simple de trouver une racine carrée est d`utiliser une calculatrice. Vous pouvez utiliser une calculatrice en ligne si vous n`avez pas de calculatrice scientifique. Cela vous donne la valeur