Comment déterminer la largeur d'un rectangle

Teneur

Il existe de nombreuses façons de trouver les dimensions manquantes d`un rectangle, et la méthode que vous utiliserez dépendra des données dont vous disposez. Tant que l`aire ou le périmètre est connu, ainsi que la longueur d`un côté du rectangle (ou le rapport entre sa longueur et sa largeur), la dimension manquante peut être déterminée. Les propriétés d`un rectangle sont telles que ces méthodes peuvent être utilisées pour déterminer sa latitude ou sa longitude.

Pas

Méthode 1 sur 4: Utilisation de la zone et de la longueur

Image intitulée Trouver la largeur d`un rectangle Étape 1

1. Écris la formule de l`aire d`un rectangle. La formule est

une = (je) (w)

$A=(l)(w)$ , par lequel

une

$une$ est égal à l`aire du rectangle,

je

$je$ est égal à la longueur du rectangle, et

w

$w$ est égal à la largeur du rectangle.

La méthode ne fonctionne que pour une surface et une longueur données du rectangle.
Cette formule est également disponible sous la forme $une = (h) (w)$ $A=(h)(w)$ , par lequel $h$ $h$ égale la hauteur du rectangle (plutôt que la longueur). Ces deux termes renvoient aux mêmes dimensions.

Image intitulée Trouver la largeur d`un rectangle Étape 2

2. Utilisez les valeurs de surface et de longueur dans la formule. Assurez-vous de substituer les bonnes variables.

Par exemple, si vous voulez trouver la largeur d`un rectangle d`une aire de 24 cm et d`une longueur de 8 cm, votre formule ressemblerait à ceci :

24 = 8 w

$24=8w$

Image intitulée Trouver la largeur d`un rectangle Étape 3

3. Résoudre pour w{style d`affichage w} $w$ . Pour ce faire, divisant chaque côté de l`équation par sa longueur.

Par exemple, dans l`équation

24 = 8 w

$24=8w$ , diviser chaque côté par 8.

24 = 8 w

$24=8w$

\frac{24}{8} = 8 w 8

${frac{24}{8}}={frac{8w}{8}}$

3 = w

$3=w$

Image intitulée Trouver la largeur d`un rectangle Étape 4

4. Écrivez votre réponse finale. N`oubliez pas de mentionner l`unité des lectures.

Par exemple, pour un rectangle d`aire

24 c m 2

$24 cm^{{2}}$ et une longueur de

8 c m

$8cm$ , devient la largeur

3 c m

$3cm$ .

Méthode 2 sur 4: Utilisation de la circonférence et de la longueur

1. Écrire la formule du périmètre d`un rectangle. La formule est

p = 2 je + 2 w

$P=2l+2w$ , par lequel

p

$p$ est égal au périmètre du rectangle,

je

$je$ est égal à la longueur du rectangle, et

w

$w$ est égal à la largeur du rectangle.

Cette méthode ne fonctionne que pour un périmètre et une longueur de rectangle donnés.
Cette formule s`écrit aussi $p = 2 (w + h)$ $P=2(l+h)$ , par lequel $h$ $h$ est égal à la hauteur du rectangle et est utilisé à la place de la longueur. Les variables $je$ $je$ et $h$ $h$ se réfèrent aux mêmes dimensions, et la propriété distributive dicte que ces deux formules, bien qu`ordonnées différemment, produisent le même résultat.

Image intitulée Trouver la largeur d`un rectangle Étape 6

2. Utilisez la circonférence et la longueur dans la formule. Assurez-vous de substituer les bonnes variables.

Par exemple, si vous vouliez trouver la largeur d`un rectangle avec une circonférence de 22 cm et une longueur de 8 cm, la formule ressemblerait à ceci :

22 = 2 (8) + 2 w

$22=2(8)+2w$

22 = 16 + 2 w

$22=16+2w$

Image intitulée Trouver la largeur d`un rectangle Étape 7

3. Résoudre w{style d`affichage w} $w$ . Pour ce faire, vous devez soustraire la longueur de chaque côté de l`équation et la diviser par 2.

Par exemple, dans l`équation

22 = 16 + 2 w

$22=16+2w$ , soustraire 16 de chaque côté et diviser par 2.

22 = 16 + 2 w

$22=16+2w$

6 = 2 w

$6=2w$

\frac{6}{2} = 2 w 2

${frac{6}{2}}={frac{2w}{2}}$

3 = w

$3=w$

Image intitulée Trouver la largeur d`un rectangle Étape 8

4. Écrivez la réponse finale. N`oubliez pas de mentionner l`unité des lectures.

Par exemple, pour un rectangle de périmètre de

22 c m

$22cm$ et une longueur de

8 c m

$8cm$ , devient la largeur

3 c m

$3cm$ .

Méthode 3 sur 4: Utilisation de la diagonale et de la longueur

Image intitulée Trouver la largeur d`un rectangle Étape 9

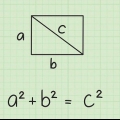
1. Écris la formule de la diagonale d`un rectangle. La formule est

ré = \sqrt{w} 2 + {je}^{2}

$D={sqrt{w^{{2}}+l^{{2}}}}$ , par lequel

ré

$ré$ est égal à la longueur de la diagonale,

je

$je$ est égal à la longueur, et

w

$w$ est égal à la largeur du rectangle.

Cette méthode ne fonctionne que pour une longueur donnée de la diagonale et la longueur d`un côté du rectangle.
Cette formule s`écrit aussi $ré = \sqrt{w} 2 + h^{2}$ $D={sqrt{w^{{2}}+h^{{2}}}}$ , par lequel $h$ $h$ est égal à la hauteur du rectangle et est utilisé à la place de la longueur. Les variables $je$ $je$ et $h$ $h$ se référer aux mêmes lectures.

Image intitulée Trouver la largeur d`un rectangle Étape 10

2. Substituer les valeurs de la diagonale et du côté dans la formule. Assurez-vous de substituer les bonnes variables.

Par exemple, lors de la détermination de la largeur d`un rectangle avec une diagonale de 5 cm et un côté de 4 cm, la formule ressemblerait à ceci :

5 = \sqrt{w} 2 + 4^{2}

$5={sqrt{w^{{2}}+4^{{2}}}}$

Image intitulée Trouver la largeur d`un rectangle Étape 11

3. Carré des deux côtés de la formule. Vous devez faire cela pour vous débarrasser du signe radical afin que l`isolement de la variable de largeur devienne plus facile.

Par exemple:

5 = \sqrt{w} 2 + 4^{2}

$5={sqrt{w^{{2}}+4^{{2}}}}$

52 = w^{2} + 4^{2}

$5^{{2}}=w^{{2}}+4^{{2}}$

25 = w 2 + 16

$25=w^{{2}}+16$

Image intitulée Trouver la largeur d`un rectangle Étape 12

4. Isoler la variable w{style d`affichage w} $w$ . Pour ce faire, en soustrayant la longueur au carré, de chaque côté de l`équation.

Par exemple, dans l`équation

25 = 16 + w 2

$25=16+w^{{2}}$ , soustraire 16 de chaque côté.

25 = 16 + w 2

$25=16+w^{{2}}$

9 = w 2

$9=w^{{2}}$

Image intitulée Trouver la largeur d`un rectangle Étape 13

5. Résoudre pour w{style d`affichage w} $w$ . Pour ce faire, déterminez la racine carrée de chaque côté de l`équation.

Par exemple:

\sqrt{9} = \sqrt{w} 2

${sqrt{9}}={sqrt{w^{{2}}}}$

3 = w

$3=w$

Image intitulée Trouver la largeur d`un rectangle Étape 14

6. Écrivez la réponse finale. N`oubliez pas de mentionner l`unité des lectures.

Par exemple, pour un rectangle de diagonale de

5 c m

$5cm$ et un côté de

4 c m

$4cm$ , devient la largeur

3 c m

$3cm$ .

Méthode 4 sur 4: Utilisation de la zone ou du périmètre et de la longueur relative

Image intitulée Trouver la largeur d`un rectangle Étape 15

1. Écrivez la formule pour l`aire ou le périmètre d`un rectangle. La formule que vous utilisez dépend des valeurs mesurées données. Si l`aire est donnée, utilisez la formule de l`aire. Si la circonférence est donnée, utilisez la formule de la circonférence.

Si la superficie ou le périmètre est inconnu, ou la relation entre la longueur et la largeur, vous ne pouvez pas utiliser cette méthode.
La formule de la zone est $une = (je) (w)$ $A=(l)(w)$ .
La formule de la circonférence est $p = 2 je + 2 w$ $P=2l+2w$ .
Par exemple, peut-être étant donné que l`aire d`un rectangle est de 24 cm, alors vous utilisez la formule de l`aire d`un rectangle.

Image intitulée Trouver la largeur d`un rectangle Étape 16

2. Écrivez l`expression qui décrit la relation entre la longueur et la largeur. Écrivez votre expression dans une comparaison avec

je

$je$ .

La relation peut être donnée en indiquant combien de fois un côté est plus grand que l`autre, ou combien d`unités plus ou moins.

Par exemple, on peut savoir que la longueur est cinq centimètres plus longue que la largeur. L`expression de la longueur devient alors

je = w + 5

$l=l+5$ .

Image intitulée Trouver la largeur d`un rectangle Étape 17

3. Remplacer la variable je{style d`affichage l} $je$ dans la formule de l`aire ou du périmètre par l`expression de la longueur. La formule n`entend plus que la variable

w

$w$ ce qui signifie que vous pouvez calculer la largeur.

Par exemple, si vous savez que l`aire est de 24 cm, et que

je = w + 5

$l=l+5$ , alors la formule ressemble à ceci:

une = (je) (w)

$A=(l)(w)$

24 = (w + 5) (w)

$24=(w+5)(w)$

Image intitulée Trouver la largeur d`un rectangle Étape 18

4. Simplifier l`équation. L`équation simplifiée peut prendre différentes formes, selon le rapport entre la longueur et la largeur, et selon que l`on opte pour la surface ou le périmètre. Essayez de faire une comparaison avec laquelle vous