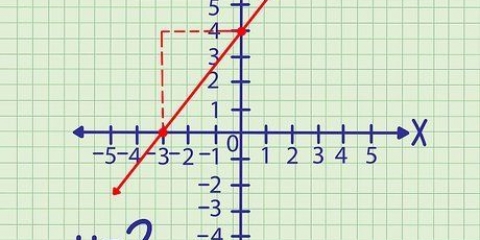
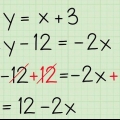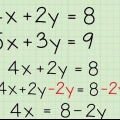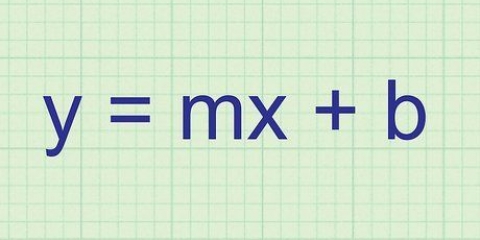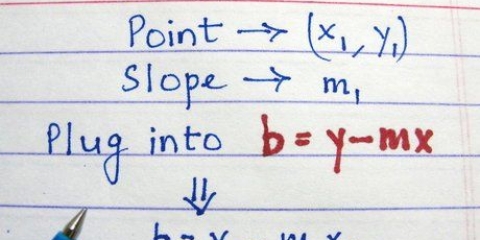Les points sont faciles à déterminer si vous avez tracé une ligne sur du papier quadrillé. Pour déterminer un point, tracez une ligne pointillée à partir de l`axe horizontal jusqu`à ce qu`elle coupe la ligne. La position où vous avez commencé la ligne sur l`axe horizontal est la coordonnée x, tandis que la coordonnée y est l`endroit où la ligne en pointillé coupe la ligne sur l`axe vertical. Par exemple : ligne je a les points (1, 5) et (-2, 4) tandis que la ligne r a les points (3, 3) et (1, -4). 
Vers la pente de la ligne je à calculer : pente = (5 - (-4))/(1 - (-2)) Soustraire : pente = 9/3 Diviser : pente = 3 La pente de la ligne r = (3 - (-4))/(3 - 1) = 7/2 
Dans cet exemple, 3 n`est pas égal à 7/2, donc ces deux droites ne sont pas parallèles. 

Par exemple : Réécrivez la ligne 4y-12x=20 comme formule de pente. Ajouter 12x aux deux côtés de l`équation : 4y - 12x + 12x = 20 + 12x Divisez chaque côté par 4 pour isoler y : 4y/4 = 12x/4 +20/4 Formule de pente : y = 3x + 5 
Dans notre exemple, la première ligne a une équation de y = 3x + 5, donc la pente est de 3. L`autre droite a une équation de y = 3x - 1 qui a également une pente de 3. Les pentes étant identiques, ces deux droites sont parallèles. Notez que si ces équations ont la même intersection avec l`axe des y, elles seraient la même ligne au lieu d`être parallèles. 

La droite que nous voulons rendre parallèle est y = -4x + 3. Dans cette équation -4 représente la variable m et donc la pente de la droite. 
Dans notre exemple, nous utilisons la coordonnée (1, -2). 
En utilisant notre exemple avec la pente (m) -4 et la coordonnée (x, y) (1, -2) cela devient : y – (-2) = -4(x – 1) 
Par exemple : y - (-2) = -4(x - 1) Deux négatifs font un positif : y + 2 = -4(x -1) Utiliser la propriété distributive pour calculer -4(x -1): y + 2 = -4x + 4. Soustraire -2 des deux côtés : y + 2 - 2 = -4x + 4 - 2 L`équation simplifiée : y = -4x + 2
Déterminer si deux droites sont parallèles
Teneur
Les lignes parallèles sont deux lignes dans un plan qui ne se couperont jamais (ce qui signifie qu`elles continueront éternellement sans jamais se toucher). Une caractéristique importante des droites parallèles est qu`elles ont des pentes identiques. La pente d`une ligne est définie comme la montée (changement des coordonnées y) sur la descente (changement des coordonnées x) d`une ligne, en d`autres termes la pente de la ligne. Les lignes parallèles sont souvent représentées par deux lignes verticales (ll). Par exemple, AB11CD indique que la ligne AB est parallèle à CD.
Pas
Méthode 1 sur 3: Comparer la pente de chaque ligne

1. Trouver la formule de la pente. La pente (pente) d`une ligne est définie par (Y2 - Oui1)/(X2 - X1) où X et Y sont les coordonnées horizontales et verticales des points sur la ligne. Vous devez déterminer deux points sur la ligne pour calculer cette formule. Le point le plus proche du bas de la ligne est (X1, Oui1) et le point le plus haut sur la ligne, au-dessus du premier point, est (X2, Oui2).
- Cette formule peut être reformulée comme l`augmentation sur la distance. C`est le changement vertical par rapport au changement horizontal, ou la pente de la ligne.
- Si une ligne pointe vers la droite et vers le haut, elle aura une pente positive.
- Si la ligne pointe vers la droite et vers le bas, elle aura une pente négative.

2. Identifiez les coordonnées X et Y de deux points sur chaque ligne. Un point sur une ligne est donné par sa coordonnée (X, Y) où X est l`emplacement sur l`axe horizontal et Y est l`emplacement sur l`axe vertical. Pour calculer la pente, vous devez déterminer deux points sur chacune des lignes en question.

3. Traiter les points pour chaque ligne dans la formule de pente. Pour calculer la pente, entrez les nombres, soustrayez et divisez. Assurez-vous d`insérer les coordonnées dans la bonne valeur x et y dans la formule.

4. Comparez les pentes de chaque ligne. Rappelez-vous que deux droites ne sont parallèles que si elles ont les mêmes pentes. Les lignes peuvent apparaître parallèles sur le papier et même être très proches du parallèle, mais si leurs pentes ne sont pas exactement égales, elles ne sont pas parallèles.
Méthode 2 sur 3: Utilisation de la formule de pente et d`intersection

1. Trouver la formule pour la pente et l`intersection d`une ligne. La formule de la pente, l`équation d`une droite. est y = mx + b, où m est la pente, b est l`intersection avec l`axe des y, et x et y sont des variables qui représentent les coordonnées sur la ligne -- généralement vous les voyez comme x et y dans l`équation. Sous cette forme, vous pouvez facilement déterminer la pente de la ligne en tant que variable `m`.
- Un exemple : réécrire 4y - 12x = 20 et y = 3x -1. L`équation 4y - 12x = 20 doit être réécrite avec l`algèbre tandis que y = 3x -1 a déjà la forme de la formule de la pente et n`a pas besoin d`être réécrite.

2. Réécrivez la formule de la ligne comme formule de pente. Souvent, la formule de la ligne que vous obtenez ne sera pas sous la forme d`un plan incliné. Il suffit d`un peu de maths et d`un réarrangement variable pour l`obtenir dans la forme de la formule de pente.

3. Comparez les pentes de chaque ligne. Rappelez-vous que si deux droites sont parallèles l`une à l`autre, elles auront exactement la même pente. En utilisant l`équation y = mx + b, où m est la pente de la ligne, vous pouvez déterminer et comparer les pentes de deux lignes.
Méthode 3 sur 3: Détermination d`une droite parallèle avec l`équation point-pente

1. Définir l`équation point-pente. Avec l`équation point-pente, vous pouvez écrire l`équation d`une ligne si vous connaissez la pente et avez une coordonnée (x, y). Vous utilisez cette formule si vous souhaitez définir une deuxième ligne parallèle sur une ligne déjà donnée avec une certaine pente. La formule est y – y1= m(x – x1) où m est la pente de la droite, x1 la coordonnée x d`un point donné sur la ligne et y1 la coordonnée y de ce point. Comme dans la formule de la pente, x et y sont des variables qui représentent des coordonnées sur la ligne - généralement, elles resteront telles que x et y dans l`équation.
- Les étapes suivantes résolvent cet exemple : Écrivez l`équation d`une droite parallèle à la droite y = -4x + 3 passant par le point (1, -2).

2. Trouver la pente de la première droite. Lors de l`écriture de l`équation d`une nouvelle droite, vous devez d`abord déterminer la pente de la droite à laquelle votre droite doit être parallèle. Assurez-vous que l`équation de la ligne d`origine est une formule de pente afin que vous connaissiez la pente (m) tout de suite.

3. Identifier un point sur la nouvelle ligne. Cette équation ne fonctionne que si vous avez une coordonnée qui passe par la nouvelle ligne. Assurez-vous de ne pas choisir une coordonnée qui se trouve sur la ligne d`origine. Si vos équations finales ont la même ordonnée à l`origine, elles ne sont pas parallèles, mais la même ligne.

4. Écrivez l`équation de la nouvelle ligne sous la forme point-pente. Rappelez-vous que la formule est : y – y1= m(x – x1). Entrez la pente et les coordonnées de votre point pour rendre l`équation de votre nouvelle ligne parallèle à la première.

5. Simplifier l`équation. Après avoir rempli les nombres, l`équation peut être simplifiée en la formule de pente plus courante. La ligne de cette équation, lorsqu`elle est dessinée dans un système de coordonnées, est parallèle à l`équation donnée.
Articles sur le sujet "Déterminer si deux droites sont parallèles"
Оцените, пожалуйста статью
Similaire
Populaire