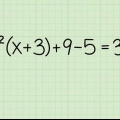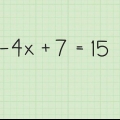Utiliser la propriété distributive pour résoudre une équation

Teneur

Pas
Des astuces

La propriété distributive est une règle en mathématiques pour simplifier une équation avec des parenthèses. Vous avez probablement appris très tôt qu`il faut d`abord faire les opérations entre parenthèses, mais avec des expressions algébriques, ce n`est pas toujours possible. La propriété distributive vous permet de multiplier le terme hors parenthèses par les termes à l`intérieur. Vous devez faire attention à bien le faire, sinon vous risquez de perdre des informations et la comparaison n`est plus correcte. Vous pouvez également utiliser la propriété distributive pour simplifier les équations avec des fractions.

Pas

Méthode 1 sur 4: Utilisation de la propriété distributive fondamentale

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 1

1. Multipliez le terme hors parenthèses par n`importe quel terme entre parenthèses. Pour ce faire, vous divisez essentiellement le terme externe entre les termes internes. Multiplier le terme hors parenthèses par le premier terme entre parenthèses. Ensuite, vous le multipliez par le deuxième terme. S`il y a plus de deux termes, continuez à distribuer le terme hors parenthèses sur tous les termes à l`intérieur des parenthèses. Il suffit de laisser les opérateurs (plus ou moins) à l`intérieur des parenthèses.

$2 (X - 3) = dix$ $2(x-3)=10$
$2 (X) - (2) (3) = dix$ $2(x)-(2)(3)=10$
$2 X - 6 = dix$ $2x-6=10$

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 2

2. Combiner des termes similaires. Avant de pouvoir résoudre l`équation, vous devez combiner des termes similaires. Combinez tous les termes numériques les uns avec les autres. De plus, vous combinez tous les termes variables séparément. Pour simplifier l`équation, ordonnez les termes de sorte que les variables soient d`un côté du signe égal et les constantes (seulement les nombres) soient de l`autre côté.

2 X - 6 = dix

$2x-6=10$ ....(problème d`origine)

2 X - 6 (+ 6) = dix (+ 6)

$2x-6(+6)=10(+6)$ .... (ajouter 6 des deux côtés)

2 X = 16

$2x=16$ .... (Variable à gauche ; constant à droite)

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 3

3. Résous l`équation. lâche

X

$X$ en divisant les deux membres de l`équation par le coefficient de la variable.

2 X = 16

$2x=16$ ....(problème d`origine)

2 X / 2 = 16 / 2

$2x/2=16/2$ ....(diviser les deux côtés par 2)

X = 8

$x=8$ ....(Solution)

Méthode 2 sur 4: Distribuer les coefficients négatifs

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 4

1. Distribuer un nombre négatif avec le signe moins. Si vous multipliez un terme ou des termes entre parenthèses par un nombre négatif, assurez-vous d`appliquer le signe moins à chaque terme à l`intérieur des parenthèses.

Rappelez-vous les règles de base pour multiplier par des nombres négatifs :

Moins x Moins = Plus.
Moins x Plus = Moins.

Regardez l`exemple suivant :

- 4 (9 - 3 X) = 48

$-4(9-3x)=48$ .... (problème d`origine)

- 4 (9) - (- 4) (3 X) = 48

$-4(9)-(-4)(3x)=48$ ....(multipliez -4 par chaque terme)

- 36 - (- 12 X) = 48

$-36-(-12x)=48$ ....(simplifier la multiplication)

- 36 + 12 X = 48

$-36+12x=48$ ....(notez que `moins -12` est le même que +12)

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 5

2. Combiner des termes similaires. Une fois la distribution terminée, vous devez ensuite simplifier l`équation en déplaçant tous les termes variables d`un côté du signe égal et tous les nombres sans variables de l`autre côté. Vous le faites au moyen d`une combinaison d`addition ou de soustraction.

- 36 + 12 X = 48

$-36+12x=48$ ....(problème d`origine)

- 36 (+ 36) + 12 X = 48 + 36

$-36(+36)+12x=48+36$ ....(ajouter 36 de chaque côté)

12 X = 84

$12x=84$ ....(simplifier l`addition pour isoler la variable)

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 6

3. Partagez pour obtenir la solution finale. Résoudre l`équation en divisant les deux côtés de l`équation par le coefficient de la variable. Cela devrait se traduire par une seule variable d`un côté de l`équation, avec le résultat de l`autre côté.

12 X = 84

$12x=84$ ....(problème d`origine)

12 X / 12 = 84 / 12

$12x/12=84/12$ ....(diviser les deux côtés par 12)

X = sept

$x=7$ ....(Solution)

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 7

4. Traiter la soustraction comme une addition (à partir de -1). Lorsque vous voyez un signe moins dans un problème d`algèbre, surtout si c`est avant une parenthèse, il dit essentiellement + (-1). Cela permet de répartir correctement le signe moins sur tous les termes entre parenthèses. Ensuite, résolvez le problème comme avant.

Par exemple, considérons le problème,

4 X - (X + 2) = 4

$4x-(x+2)=4$ . Pour vous assurer que vous avez correctement distribué le signe moins, réécrivez le problème comme ceci :

4 X + (- 1) (X + 2) = 4

$4x+(-1)(x+2)=4$

Ensuite, vous répartissez -1 sur les termes entre parenthèses, comme suit :

4 X + (- 1) (X + 2) = 4

$4x+(-1)(x+2)=4$ ....(question modifiée)

4 X - X - 2 = 4

$4x-x-2=4$ ....(multiplier -1 par x et par 2)

3 X - 2 = 4

$3x-2=4$ ....(combiner les termes)

3 X - 2 + 2 = 4 + 2

$3x-2+2=4+2$ ....(ajouter 2 des deux côtés)

3 X = 6

$3x=6$ ....(simplifier les termes)

3 X / 3 = 6 / 3

$3x/3=6/3$ ....(diviser les deux côtés par 3)

X = 2

$x=2$ ....(Solution)

Méthode 3 sur 4: Utiliser la propriété distributive pour simplifier les fractions

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 8

1. Découvrez s`il existe des coefficients fractionnaires ou des constantes. Parfois, vous devrez peut-être résoudre un problème avec des fractions en tant que coefficients ou constantes. Vous pouvez les laisser tels quels et leur appliquer les règles fondamentales de l`algèbre, pour résoudre le problème. Cependant, en utilisant la propriété distributive, vous pouvez souvent simplifier la solution en convertissant les fractions en nombres entiers.

Découvrez l`exemple suivant $X - 3 = \frac{X}{3} + \frac{1}{6}$ $x-3={frac{x}{3}}+{frac{1}{6}}$ . Les fractions de cet exemple sont $\frac{X}{3}$ ${frac{x}{3}}$ et $\frac{1}{6}$ ${frac{1}{6}}$ .

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 9

2. Trouver le plus petit commun multiple (LCM) pour tous les dénominateurs. A cette étape, vous pouvez ignorer tous les entiers. Il suffit de regarder les fractions et de déterminer le LCF pour tous les dénominateurs. Déterminer le kgf en cherchant le plus petit nombre qui est un multiple des dénominateurs des deux fractions de l`équation. Dans cet exemple, les dénominateurs sont 3 et 6, donc 6 est le kgf.

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 10

3. Multiplier tous les termes de l`équation par le kgf. N`oubliez pas que vous pouvez appliquer n`importe quelle opération à une équation mathématique, tant que vous le faites des deux côtés. En multipliant chaque terme de l`équation par le lcg, les termes s`annulent et "deviennent" des entiers. Placez vos parenthèses autour de l`ensemble des côtés gauche et droit de l`équation, puis effectuez la distribution :

X - 3 = \frac{X}{3} + \frac{1}{6}

$x-3={frac{x}{3}}+{frac{1}{6}}$ ....(équation originale)

(X - 3) = (\frac{X}{3} + \frac{1}{6})

$(x-3)=({frac{x}{3}}+{frac{1}{6}})$ ....(appliquer des parenthèses)

6 (X - 3) = 6 (\frac{X}{3} + \frac{1}{6})

$6(x-3)=6({frac{x}{3}}+{frac{1}{6}})$ ....(multiplier les deux côtés par le kgf)

6 X - 6 (3) = 6 (\frac{X}{3}) + 6 (\frac{1}{6})

$6x-6(3)=6({frac{x}{3}})+6({frac{1}{6}})$ ....(distribuer la multiplication)

6 X - 18 = 2 X + 1

$6x-18=2x+1$ ....(simplifier la multiplication)

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 11

4. Combiner des termes similaires. Combinez tous les termes de sorte que toutes les variables soient d`un côté de l`équation et toutes les constantes de l`autre. Utilisez les opérations d`addition et de soustraction de base pour déplacer les termes d`un côté de l`équation à l`autre.

6 X - 18 = 2 X + 1

$6x-18=2x+1$ ....(problème simplifié)

6 X - 2 X - 18 = 2 X - 2 X + 1

$6x-2x-18=2x-2x+1$ ....(soustrayez 2x des deux côtés)

4 X - 18 = 1

$4x-18=1$ ....(simplifier moins la somme)

4 X - 18 + 18 = 1 + 18

$4x-18+18=1+18$ ....(ajouter 18 des deux côtés)

4 X = 19

$4x=19$ ....(addition simplifiée)

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 12

5. Résous l`équation. Trouvez la solution finale en divisant les deux côtés de l`équation par le coefficient de la variable. Cela vous laisse avec x d`un côté de l`équation et la solution numérique de l`autre.

4 X = 19

$4x=19$ ....(problème personnalisé)

4 X / 4 = 19 / 4

$4x/4=19/4$ ....(diviser les deux côtés par 4)

X = \frac{19}{4} ou 4 \frac{3}{4}

$x={frac{19}{4}}{text{ ou }}4{frac{3}{4}}$ ....(solution finale)

Méthode 4 sur 4: Distribuer une fraction avec une équation

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 13

1. Interpréter une fraction avec une équation comme une division distribuée. Parfois, vous voyez un problème avec plusieurs termes dans le numérateur d`une fraction, au-dessus d`un dénominateur commun. Vous devez traiter cela comme un problème distributif et appliquer le dénominateur à chaque terme du numérateur. Vous pouvez réécrire la fraction pour montrer la distribution. Comme suit:

$4 X + 8 2 = 4$ ${frac{4x+8}{2}}=4$ .....(problème d`origine)
$4 X 2 + \frac{8}{2} = 4$ ${frac{4x}{2}}+{frac{8}{2}}=4$ .....(multiplier le dénominateur par chaque terme du numérateur)

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 14

2. Simplifier chaque numérateur en tant que fraction distincte. Après avoir distribué le diviseur sur chaque terme, vous pouvez ensuite simplifier chaque terme individuellement.

4 X 2 + \frac{8}{2} = 4

${frac{4x}{2}}+{frac{8}{2}}=4$ .....(problème personnalisé)

2 X + 4 = 4

$2x+4=4$ .....(simplifier les fractions)

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 15

3. Isoler la variable. Continuez à résoudre le problème en isolant la variable d`un côté de l`équation et en déplaçant les termes constants de l`autre côté. Pour ce faire, par une combinaison d`addition et de soustraction, si nécessaire.

2 X + 4 = 4

$2x+4=4$ .....(problème personnalisé)

2 X + 4 - 4 = 4 - 4

$2x+4-4=4-4$ .....(soustrayez 4 des deux côtés)

2 X = 0

$2x=0$ .....(isoler x d`un côté)

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 16

4. Diviser par le coefficient pour résoudre le problème. Dans la dernière étape, vous divisez par le coefficient de la variable. Cela donne la solution finale, avec la variable unique d`un côté de l`équation et la solution numérique de l`autre.

2 X = 0

$2x=0$ .....(problème personnalisé)

2 X / 2 = 0 / 2

$2x/2=0/2$ .....(diviser les deux côtés par 2)

X = 0

$x=0$ .....(Solution)

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 17

5. Évitez l`erreur courante de ne partager qu`un seul terme. Il est tentant (mais incorrect) de diviser le premier terme du numérateur par le dénominateur et d`éliminer la fraction. Une erreur comme celle-ci ressemblerait à ceci pour le problème ci-dessus :

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(problème d`origine)

2 X + 8 = 4

$2x+8=4$ .....(seulement 4x est divisé par 2, au lieu du compteur complet)

2 X + 8 - 8 = 4 - 8

$2x+8-8=4-8$

2 X = - 4

$2x=-4$

X = - 2

$x=-2$ ..... (mauvaise solution)

Image intitulée Utiliser la propriété distributive pour résoudre une équation Étape 18

6. Vérifiez l`exactitude de votre solution. Vous pouvez toujours vérifier votre travail en insérant votre solution dans le problème d`origine. Quand on veut simplifier, il faut arriver à un vrai constat. Si vous simplifiez et obtenez une déclaration incorrecte comme réponse, alors votre solution est incorrecte. Dans cet exemple, vous testez les deux solutions pour x = 0 et x =-2 pour voir laquelle est correcte.

Commencer par la solution x=0 :

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(problème d`origine)

4 (0) + 8 2 = 4

${frac{4(0)+8}{2}}=4$ .....(remplacer 0 par x)

0 + 8 2 = 4

${frac{0+8}{2}}=4$

\frac{8}{2} = 4

${frac{8}{2}}=4$

4 = 4

$4=4$ .....(Vrai. C`est la bonne solution.)

Essayez la "mauvaise solution pour x=-2 :

4 X + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(problème d`origine)

4 (- 2) + 8 2 = 4

${frac{4(-2)+8}{2}}=4$ .....(entrez -2 pour x)

- 8 + 8 2 = 4

${frac{-8+8}{2}}=4$

\frac{0}{2} = 4

${frac{0}{2}}=4$

0 = 4

$0=4$ .....(Déclaration incorrecte. Donc x=-2 est faux.)

Des astuces

Vous pouvez également utiliser la propriété distributive pour simplifier certaines multiplications. Vous pouvez diviser les nombres en dizaines avec un reste pour faciliter le calcul mental. Par exemple, vous pouvez réécrire 8 x 16 en 8 (10+6). C`est alors simplement 80 + 48 = 128. Un autre exemple, 7 x 24 = 7(20 + 4) = 7(20) + 7(4) = 140 + 28 = 168. Pratiquez-les par cœur et le calcul mental deviendra beaucoup plus facile.