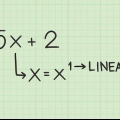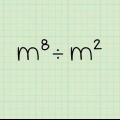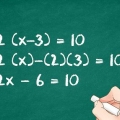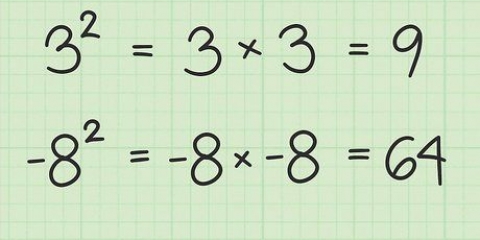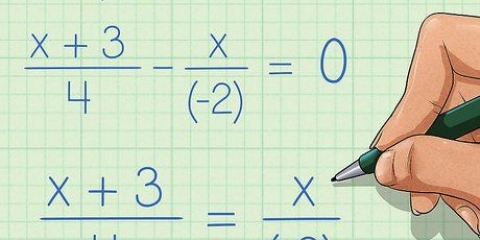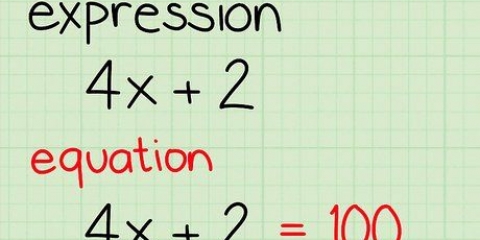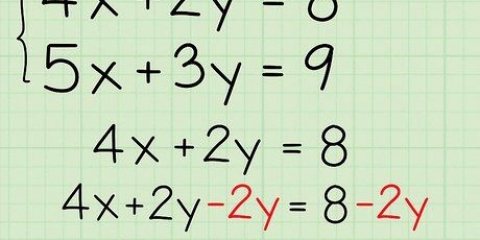Dix à la puissance trois











Comme indiqué ici, vous pouvez continuer à multiplier la base par le produit de chacune des premières paires de nombres jusqu`à ce que vous obteniez la réponse finale. Continuez simplement à multiplier les deux premiers nombres, puis multipliez cette réponse par le nombre suivant de la séquence. Ceci est vrai pour tout exposant. Lorsque vous avez terminé avec l`exemple, vous obtenez  .
. 




Utilisez un moteur de recherche comme Startpage, Duckduckgo ou Google pour trouver la réponse. Vous pouvez utiliser le bouton `^` de votre ordinateur, tablette ou smartphone pour saisir l`expression dans le champ de recherche, et vous verrez immédiatement la réponse et des suggestions d`expressions similaires à explorer (Duckduckgo affiche même une calculatrice complète). 





Puisque tout est le même nombre, mais multiplié, nous pouvons combiner ceux-ci : 




Puisque les bases sont les mêmes, vous pouvez simplement les additionner : 




Comme vous le verrez dans un instant, tout nombre faisant partie d`une fraction, comme  , être réécrit comme
, être réécrit comme  . Les exposants négatifs forment des fractions.
. Les exposants négatifs forment des fractions. 
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Rappelez-vous qu`un nombre sans puissance a un exposant de 1
Rappelez-vous qu`un nombre sans puissance a un exposant de 1 =
= 
 =
= 




![Résoudre les exposants x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Résoudre les exposants ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)



Résoudre les exposants
Teneur
Les exposants sont utilisés lorsqu`un nombre est multiplié par lui-même. À la place de 



Pas
Méthode 1 sur 3: Résolution d`exposants simples

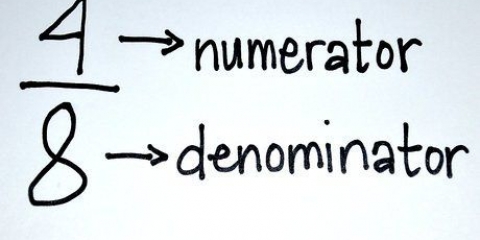
1. Apprenez les termes et le vocabulaire corrects pour les problèmes exponentiels. Avez-vous un exposant comme  , alors vous travaillez avec deux parties simples. Le numéro de châssis ici est un 2, ou le base. Ce nombre est élevé à la puissance 3, également connu sous le nom de exposant ou Puissance. Parlons-nous de
, alors vous travaillez avec deux parties simples. Le numéro de châssis ici est un 2, ou le base. Ce nombre est élevé à la puissance 3, également connu sous le nom de exposant ou Puissance. Parlons-nous de  , puis nous disons "deux à la troisième", "deux à la troisième puissance" ou "deux augmentations à la troisième puissance".`
, puis nous disons "deux à la troisième", "deux à la troisième puissance" ou "deux augmentations à la troisième puissance".`
 , alors vous travaillez avec deux parties simples. Le numéro de châssis ici est un 2, ou le base. Ce nombre est élevé à la puissance 3, également connu sous le nom de exposant ou Puissance. Parlons-nous de
, alors vous travaillez avec deux parties simples. Le numéro de châssis ici est un 2, ou le base. Ce nombre est élevé à la puissance 3, également connu sous le nom de exposant ou Puissance. Parlons-nous de  , puis nous disons "deux à la troisième", "deux à la troisième puissance" ou "deux augmentations à la troisième puissance".`
, puis nous disons "deux à la troisième", "deux à la troisième puissance" ou "deux augmentations à la troisième puissance".` - Si un nombre est élevé à la puissance 2, comme par exemple
, alors vous pouvez aussi dire que le nombre est au carré est, comme `cinq au carré.`
- Si un nombre est élevé à la troisième puissance, comme
, alors vous pouvez aussi dire que le nombre a nombre de cubes est.
- Si un nombre sans exposant est mentionné, comme 4, par exemple, alors il est théoriquement à la première puissance et peut être réécrit comme
.
- Si l`exposant est égal à 0 et qu`un « nombre (non nul) » est élevé à la « puissance zéro », alors l`entier est égal à 1, car
ou même quelque chose comme
Plus d`informations à ce sujet dans la section "Conseils".

2. Multiplier la base le nombre de fois par elle-même comme indiqué par l`exposant. Si vous devez résoudre une puissance à la main, vous commencez par la réécrire sous forme de multiplication. Vous multipliez la base le nombre de fois par elle-même, comme indiqué par l`exposant. Alors, avez-vous  puis tu multiplies trois quatre fois par lui-même
puis tu multiplies trois quatre fois par lui-même  . Voici quelques autres exemples :
. Voici quelques autres exemples :
 puis tu multiplies trois quatre fois par lui-même
puis tu multiplies trois quatre fois par lui-même  . Voici quelques autres exemples :
. Voici quelques autres exemples :



3. Résoudre une expression : Multipliez les deux premiers nombres pour obtenir le produit. Par exemple, avec  , est-ce que tu commences par
, est-ce que tu commences par  Cela semble être une tâche fastidieuse, mais faites-le étape par étape. Commencez par multiplier les deux premiers quatre. Remplacez ensuite les deux quatre par la réponse comme indiqué ci-dessous :
Cela semble être une tâche fastidieuse, mais faites-le étape par étape. Commencez par multiplier les deux premiers quatre. Remplacez ensuite les deux quatre par la réponse comme indiqué ci-dessous :
 , est-ce que tu commences par
, est-ce que tu commences par  Cela semble être une tâche fastidieuse, mais faites-le étape par étape. Commencez par multiplier les deux premiers quatre. Remplacez ensuite les deux quatre par la réponse comme indiqué ci-dessous :
Cela semble être une tâche fastidieuse, mais faites-le étape par étape. Commencez par multiplier les deux premiers quatre. Remplacez ensuite les deux quatre par la réponse comme indiqué ci-dessous :



4. Multipliez la réponse de la première paire (16) par le nombre suivant. Continuez à multiplier les nombres pour "faire grandir" votre exposant. En poursuivant notre exemple, nous multiplions 16 par les 4 suivants pour que :






 .
.
5. Essayez également les exemples suivants et vérifiez vos réponses avec une calculatrice.




6. Utilisez le `exp,` `X m  ` ou `^` de votre calculatrice pour les exposants. Il est presque impossible de trouver des exposants plus grands, tels que
` ou `^` de votre calculatrice pour les exposants. Il est presque impossible de trouver des exposants plus grands, tels que  à la main, mais les calculatrices peuvent gérer cela facilement. Le bouton pour cela est généralement indiqué assez clairement. La calculatrice Windows peut être développée en une calculatrice scientifique en cliquant sur l`onglet « Affichage » de la calculatrice et en sélectionnant « Scientifique ». Si vous souhaitez récupérer la calculatrice par défaut, cliquez à nouveau sur « Afficher » et sélectionnez « Par défaut ».
à la main, mais les calculatrices peuvent gérer cela facilement. Le bouton pour cela est généralement indiqué assez clairement. La calculatrice Windows peut être développée en une calculatrice scientifique en cliquant sur l`onglet « Affichage » de la calculatrice et en sélectionnant « Scientifique ». Si vous souhaitez récupérer la calculatrice par défaut, cliquez à nouveau sur « Afficher » et sélectionnez « Par défaut ».
 ` ou `^` de votre calculatrice pour les exposants. Il est presque impossible de trouver des exposants plus grands, tels que
` ou `^` de votre calculatrice pour les exposants. Il est presque impossible de trouver des exposants plus grands, tels que  à la main, mais les calculatrices peuvent gérer cela facilement. Le bouton pour cela est généralement indiqué assez clairement. La calculatrice Windows peut être développée en une calculatrice scientifique en cliquant sur l`onglet « Affichage » de la calculatrice et en sélectionnant « Scientifique ». Si vous souhaitez récupérer la calculatrice par défaut, cliquez à nouveau sur « Afficher » et sélectionnez « Par défaut ».
à la main, mais les calculatrices peuvent gérer cela facilement. Le bouton pour cela est généralement indiqué assez clairement. La calculatrice Windows peut être développée en une calculatrice scientifique en cliquant sur l`onglet « Affichage » de la calculatrice et en sélectionnant « Scientifique ». Si vous souhaitez récupérer la calculatrice par défaut, cliquez à nouveau sur « Afficher » et sélectionnez « Par défaut ».Méthode 2 sur 3: Ajouter, soustraire et multiplier des exposants

1. Vous ne pouvez additionner ou soustraire des nombres de puissance les uns des autres que s`ils ont la même base et le même exposant. Si vous avez affaire à des bases et des exposants identiques, tels que  , alors vous pouvez simplifier l`addition des termes à une multiplication. N`oublie pas ça
, alors vous pouvez simplifier l`addition des termes à une multiplication. N`oublie pas ça  peut être considéré comme
peut être considéré comme  , de sorte que
, de sorte que  en ajoutant, où `1 de cela + 1 de cela = 2 de cela`, quel que soit `cela` puisse être. Additionnez simplement le nombre de termes similaires (ceux avec la base et l`exposant identiques) et multipliez la somme par cette expression exponentielle. Vous pouvez alors
en ajoutant, où `1 de cela + 1 de cela = 2 de cela`, quel que soit `cela` puisse être. Additionnez simplement le nombre de termes similaires (ceux avec la base et l`exposant identiques) et multipliez la somme par cette expression exponentielle. Vous pouvez alors  résoudre et multiplier cette réponse par deux. Rappelez-vous que cela est possible parce qu`une multiplication n`est rien de plus que la réécriture d`une addition, car
résoudre et multiplier cette réponse par deux. Rappelez-vous que cela est possible parce qu`une multiplication n`est rien de plus que la réécriture d`une addition, car  . Voici quelques exemples:
. Voici quelques exemples:
 , alors vous pouvez simplifier l`addition des termes à une multiplication. N`oublie pas ça
, alors vous pouvez simplifier l`addition des termes à une multiplication. N`oublie pas ça  peut être considéré comme
peut être considéré comme  , de sorte que
, de sorte que  en ajoutant, où `1 de cela + 1 de cela = 2 de cela`, quel que soit `cela` puisse être. Additionnez simplement le nombre de termes similaires (ceux avec la base et l`exposant identiques) et multipliez la somme par cette expression exponentielle. Vous pouvez alors
en ajoutant, où `1 de cela + 1 de cela = 2 de cela`, quel que soit `cela` puisse être. Additionnez simplement le nombre de termes similaires (ceux avec la base et l`exposant identiques) et multipliez la somme par cette expression exponentielle. Vous pouvez alors  résoudre et multiplier cette réponse par deux. Rappelez-vous que cela est possible parce qu`une multiplication n`est rien de plus que la réécriture d`une addition, car
résoudre et multiplier cette réponse par deux. Rappelez-vous que cela est possible parce qu`une multiplication n`est rien de plus que la réécriture d`une addition, car  . Voici quelques exemples:
. Voici quelques exemples: 
2. Multiplier des nombres de même base en additionnant les exposants. Si vous avez deux exposants avec la même base, comme  , ensuite il suffit d`additionner les deux exposants avec la même base. Alors,
, ensuite il suffit d`additionner les deux exposants avec la même base. Alors, . Si vous trouvez cela un peu étrange, décomposez-le en parties plus petites pour comprendre comment le système fonctionne :
. Si vous trouvez cela un peu étrange, décomposez-le en parties plus petites pour comprendre comment le système fonctionne :
 , ensuite il suffit d`additionner les deux exposants avec la même base. Alors,
, ensuite il suffit d`additionner les deux exposants avec la même base. Alors, . Si vous trouvez cela un peu étrange, décomposez-le en parties plus petites pour comprendre comment le système fonctionne :
. Si vous trouvez cela un peu étrange, décomposez-le en parties plus petites pour comprendre comment le système fonctionne :






3. Multiplier un nombre exponentiel élevé à une autre puissance, comme ( X 2 ) 5  . Si vous élevez un nombre à une certaine puissance et que le tout est élevé à une certaine puissance, multipliez simplement les deux exposants. Alors,
. Si vous élevez un nombre à une certaine puissance et que le tout est élevé à une certaine puissance, multipliez simplement les deux exposants. Alors,  . Si vous êtes confus, repensez à ce que ces symboles signifient réellement.
. Si vous êtes confus, repensez à ce que ces symboles signifient réellement.  signifie simplement que vous
signifie simplement que vous  Se multiplie 5 fois par lui-même, donc :
Se multiplie 5 fois par lui-même, donc :
 . Si vous élevez un nombre à une certaine puissance et que le tout est élevé à une certaine puissance, multipliez simplement les deux exposants. Alors,
. Si vous élevez un nombre à une certaine puissance et que le tout est élevé à une certaine puissance, multipliez simplement les deux exposants. Alors,  . Si vous êtes confus, repensez à ce que ces symboles signifient réellement.
. Si vous êtes confus, repensez à ce que ces symboles signifient réellement.  signifie simplement que vous
signifie simplement que vous  Se multiplie 5 fois par lui-même, donc :
Se multiplie 5 fois par lui-même, donc :



4. Considérez les exposants négatifs comme des fractions ou l`inverse du nombre. Je ne sais pas ce qu`est une réciproque, pas de problème. Si vous avez affaire à un exposant négatif, tel que  , puis rendez l`exposant positif et placez-le comme dénominateur en dessous de un, ce qui donne
, puis rendez l`exposant positif et placez-le comme dénominateur en dessous de un, ce qui donne  . Voici quelques exemples supplémentaires :
. Voici quelques exemples supplémentaires :
 , puis rendez l`exposant positif et placez-le comme dénominateur en dessous de un, ce qui donne
, puis rendez l`exposant positif et placez-le comme dénominateur en dessous de un, ce qui donne  . Voici quelques exemples supplémentaires :
. Voici quelques exemples supplémentaires :


5. Divisez deux nombres avec la même base en soustrayant les exposants. La division est l`opposé de la multiplication, et bien qu`ils ne soient pas résolus exactement comme des opposés, ils sont ici. Si vous avez affaire à l`équation  , il suffit de soustraire l`exposant du haut de celui du bas et de laisser la base telle quelle. Alors,
, il suffit de soustraire l`exposant du haut de celui du bas et de laisser la base telle quelle. Alors,  , ou 16.
, ou 16.
 , il suffit de soustraire l`exposant du haut de celui du bas et de laisser la base telle quelle. Alors,
, il suffit de soustraire l`exposant du haut de celui du bas et de laisser la base telle quelle. Alors,  , ou 16.
, ou 16. , être réécrit comme
, être réécrit comme  . Les exposants négatifs forment des fractions.
. Les exposants négatifs forment des fractions.
6. Essayez quelques exercices pratiques pour vous habituer à travailler avec des nombres de puissance. Les exercices suivants mettent en pratique tout ce qui a été discuté jusqu`à présent. Pour la réponse, il suffit de sélectionner la ligne qui contient le problème.
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Rappelez-vous qu`un nombre sans puissance a un exposant de 1
Rappelez-vous qu`un nombre sans puissance a un exposant de 1 =
= 
 =
= 
Méthode 3 sur 3: Résoudre des fractions sous forme de nombres de puissance

1. Traitez les fractions sous forme de nombres de puissance, tels que X 1 2  comme racine carrée.
comme racine carrée.  est en fait exactement le même que
est en fait exactement le même que  . Ceci est vrai quel que soit le dénominateur de la fraction, donc
. Ceci est vrai quel que soit le dénominateur de la fraction, donc  devient la racine quadratique de x, également écrite comme
devient la racine quadratique de x, également écrite comme ![Résoudre les exposants {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
.
 comme racine carrée.
comme racine carrée.  est en fait exactement le même que
est en fait exactement le même que  . Ceci est vrai quel que soit le dénominateur de la fraction, donc
. Ceci est vrai quel que soit le dénominateur de la fraction, donc  devient la racine quadratique de x, également écrite comme
devient la racine quadratique de x, également écrite comme ![Résoudre les exposants {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
. - Les racines sont l`inverse des exposants. Par exemple, si vous prenez la réponse de
à la quatrième puissance, puis vous revenez à
, et peut donc
aussi être écrit comme
. Un autre exemple est
puis
Et ainsi
.

2. Faire du numérateur un exposant normal pour une fraction mixte. peut sembler impossible, mais c`est facile si vous vous souvenez comment les exposants sont multipliés. Faire de la base une racine carrée, comme une fraction normale, et élever le tout à la puissance au sommet de la fraction. Si vous avez du mal à vous en souvenir, reprenez la théorie. Enfin ça s`applique
peut sembler impossible, mais c`est facile si vous vous souvenez comment les exposants sont multipliés. Faire de la base une racine carrée, comme une fraction normale, et élever le tout à la puissance au sommet de la fraction. Si vous avez du mal à vous en souvenir, reprenez la théorie. Enfin ça s`applique  est juste égal
est juste égal  Par exemple:
Par exemple:
 peut sembler impossible, mais c`est facile si vous vous souvenez comment les exposants sont multipliés. Faire de la base une racine carrée, comme une fraction normale, et élever le tout à la puissance au sommet de la fraction. Si vous avez du mal à vous en souvenir, reprenez la théorie. Enfin ça s`applique
peut sembler impossible, mais c`est facile si vous vous souvenez comment les exposants sont multipliés. Faire de la base une racine carrée, comme une fraction normale, et élever le tout à la puissance au sommet de la fraction. Si vous avez du mal à vous en souvenir, reprenez la théorie. Enfin ça s`applique  est juste égal
est juste égal  Par exemple:
Par exemple:

![Résoudre les exposants x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Résoudre les exposants ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)

3. Vous pouvez ajouter, soustraire et multiplier des fractions sous forme de nombres de puissance - comme vous le feriez normalement. Il est beaucoup plus facile d`ajouter ou de soustraire les exposants avant de les résoudre ou de les convertir en racines carrées. Si la base est la même et l`exposant est le même, alors vous pouvez simplement les ajouter et les soustraire. Si seule la base est la même, alors vous pouvez multiplier et diviser les exposants comme d`habitude, tant que vous tenez compte comment additionner et soustraire des fractions. Par exemple:


Des astuces
- La plupart des calculatrices ont un bouton pour les exposants - appuyez après avoir entré la base - pour résoudre les problèmes de nombre de puissance.Habituellement, cela ressemble à un ^ ou x^y.
- « Simplifier » en mathématiques signifie faire les modifications nécessaires pour obtenir la forme la plus simple des expressions en question.
- 1 est l`élément d`identité des exposants. Cela signifie que tout nombre réel élevé à la puissance 1 (à la première puissance) est le nombre lui-même, par exemple :
De plus, 1 est l`élément d`identité de la multiplication (1 comme multiplicateur, tel que
), et de la division (1 comme dividende, comme
.
- La base zéro à zéro (0) n`est pas définie (anglais : dne, n`existe pas). Les ordinateurs ou les calculatrices renverront alors une "erreur". Rappelez-vous que tout nombre non nul élevé à la puissance 0 est toujours égal à 1,
- Par exemple, les mathématiques supérieures pour les nombres imaginaires sont,
, par lequel
; e est une constante continue irrationnelle égale à 2,71828..., et a est une constante arbitraire. La preuve peut être trouvée dans la plupart des livres de mathématiques supérieures.
Mises en garde
- Une augmentation exponentielle fait monter le produit de plus en plus vite, de sorte que la réponse peut sembler fausse, alors qu`elle est correcte. (Vérifiez cela en traçant une fonction exponentielle, par exemple.: 2, si x a une plage de valeurs différentes).
Articles sur le sujet "Résoudre les exposants"
Оцените, пожалуйста статью
Populaire