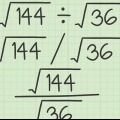Autre exemple : on veut trouver la racine carrée de 25 (√(25)). Cela signifie que nous devons trouver le nombre qui multiplié par lui-même a 25 comme produit. Puisque 5 = 5 × 5 = 25, on peut dire que √(25) = 5. Vous pouvez également considérer cela comme "défaire" un carré (ou un nombre de puissance). Par exemple, si nous voulons trouver la racine carrée de 64 (√64), considérons 64 comme 8. d`abord. Puisqu`un radical "élimine" en principe un carré, on peut dire que (64) = √(8) = 8. 
D`autre part, les nombres qui ne donnent pas des nombres entiers après la racine carrée sont appelés, carré imparfait. Lorsque vous prenez la racine carrée de l`un de ces nombres, vous obtenez généralement une décimale ou une fraction. Parfois, les décimales impliquées peuvent devenir vraiment désordonnées. Par exemple, (13) = 3.605551275464… 
1 = 1 × 1 = 1 2 = 2 × 2 = 4 3 = 3 × 3 = 9 4 = 4 × 4 = 16 5 = 5 × 5 = 25 6 = 6 × 6 = 36 7 = 7 × 7 = 49 8 = 8 × 8 = 64 9 = 9 × 9 = 81 10 = 10 × 10 = 100 11 = 11 × 11 = 121 12 = 12 × 12 = 144 
Supposons que vous vouliez calculer la racine carrée de 900. À première vue, cela semble très difficile! Cependant, ce n`est pas difficile si l`on factorise 900. Les « facteurs » sont ces nombres qui peuvent se multiplier pour former un autre nombre. Par exemple, puisque 6 est le produit de 1 × 6 et 2 × 3, les facteurs de 6 sont les nombres 1, 2, 3 et 6. Au lieu de calculer avec le nombre 900, ce qui est un peu gênant, nous l`écrivons comme 9 × 100. Maintenant, puisque 9 est un carré parfait et séparé de 100, on peut prendre sa racine carrée. (9 × 100) = √(9) × √(100) = 3 × √(100). En d`autres termes, (900) = 3√(100). Nous pouvons encore simplifier ces deux étapes en divisant 100 en facteurs 25 et 4. (100) = (25 × 4) = √(25) × √(4) = 5 × 2 = 10. On peut donc dire que (900) = 3(10) = 30. 
Remarque : bien que les nombres imaginaires ne puissent pas être représentés par des nombres normaux, ils peuvent toujours être traités comme des nombres normaux à bien des égards. Par exemple, les racines de nombres négatifs peuvent être mises au carré pour donner ces nombres négatifs comme n`importe quelle autre racine carrée. Par exemple : je = -1. 

Dans notre exemple, nous divisons 6,45 en paires comme ceci : 6-,45-00. Notez qu`il y a un numéro `restant` sur la gauche &mdash c`est le point. 
Dans notre exemple, le premier groupe de 6-,45-00 est le 6. Le plus grand nombre inférieur ou égal à 6 est 2 — 2 = 4. Écrivez un `2` au-dessus du 6 en dessous du radical. 
Dans notre exemple, nous commencerons par le double de 2, le premier chiffre de notre réponse. 2 × 2 = 4. Ensuite, nous soustrayons 4 de 6 (notre premier "groupe") et nous obtenons 2 comme réponse. Ensuite, nous déplaçons le groupe suivant (45) d`une ligne vers le bas pour obtenir 245. Enfin, nous écrirons un autre 4 sur la gauche, en laissant un peu d`espace à ajouter à la fin, comme ceci : 4_. 
Dans notre exemple, nous recherchons le nombre à remplir en 4_ × _ ; qui rend la réponse aussi grande que possible, mais toujours inférieure ou égale à 245. Dans ce cas, la réponse est 5. 45 × 5 = 225, tandis que 46 × 6 = 276. 
Nous continuons avec notre exemple et continuons avec 225 - 245 = 20. Ensuite, nous abaissons la prochaine paire de chiffres, 00, pour faire 2000. Si on double le nombre au dessus du radical, on obtient 25 × 2 = 50. On résout l`inconnue en 50_ × _ =/< 2000, alors on obtient 3 comme réponse. À ce stade, nous avons `253` au-dessus du radical - en répétant cela, 9 est le chiffre suivant. 
Dans notre exemple, le nombre sous le signe radical est 6,45, nous déplaçons donc simplement la virgule vers le haut et la plaçons entre 2 et 5 de notre réponse, ce qui nous donne 2 539 rendements. 

Dans notre exemple de problème, une estimation raisonnable pour la racine carrée de 40 est peut-être 6.4, car d`après ce qui précède, nous savons que la réponse est probablement légèrement plus proche de 6 que de 7. 
Multipliez 6,4 par lui-même, donc 6,4 × 6,4 = 40,96, qui est légèrement plus grand que le nombre d`origine. Ensuite, nous multiplions le nombre par un dixième de moins que notre estimation ci-dessus (car notre réponse était trop élevée), et nous obtenons 6,3 × 6,3 = 39,69. C`est légèrement inférieur à notre nombre d`origine. Cela signifie que la racine carrée de 40 est quelque part entre 6,3 et 6,4 gésir. De plus, comme 39,69 est plus proche de 40 que de 40,96, vous savez que la racine carrée est plus proche de 6,3 que de 6,4. 
Dans notre exemple, choisissons 6,33 pour notre estimation à deux décimales. Carré 6,33 et vous obtenez 6,33 × 6,33 = 40,0689. Étant donné qu`il est légèrement supérieur à notre nombre d`origine, nous allons essayer un nombre légèrement inférieur, tel que 6,32. 6,32 × 6,32 = 39,9424. C`est légèrement en dessous de notre nombre d`origine, donc nous savons que la racine carrée exacte entre 6.33 et 6.32 gésir. Si nous voulions aller plus loin, nous pouvons continuer à utiliser la même approche pour obtenir une réponse de plus en plus précise.
Résoudre les racines carrées
Teneur
Alors que la vue intimidante d`un symbole de racine carrée peut faire grincer des dents les personnes souffrant d`anxiété mathématique, les problèmes de racine carrée ne sont pas aussi difficiles à résoudre qu`il y paraît à première vue. De simples problèmes de racine carrée peuvent souvent être résolus aussi facilement que de simples problèmes de multiplication et de division. D`un autre côté, les problèmes de racine carrée plus complexes peuvent nécessiter un peu plus de travail, mais avec la bonne approche, même ces problèmes peuvent être résolus facilement. Commencez à pratiquer les problèmes de racine carrée aujourd`hui pour apprendre cette compétence mathématique qui peut être nouvelle pour vous!
Pas
Partie 1 sur 3: Comprendre les pouvoirs et les racines

1. Carré un nombre en le multipliant par lui-même. Pour comprendre les racines, il vaut mieux commencer par les carrés. Les carrés sont faciles - mettre un nombre au carré équivaut à le multiplier par lui-même. Par exemple : 3 au carré équivaut à 3 × 3 = 9, et 9 au carré équivaut à 9 × 9 = 81. Les carrés sont indiqués par un petit « 2 » au-dessus et à droite du nombre au carré — comme ceci : 3, 9, 100, etc.
- Essayez de mettre au carré quelques nombres vous-même pour tester ce concept. Rappelez-vous que la quadrature d`un nombre n`est rien de plus que de multiplier ce nombre par lui-même. Vous pouvez le faire même avec des nombres négatifs. Dans tous les cas, la réponse sera toujours positive. Par exemple : -8 = -8 × -8 = 64.

2. Pour trouver la racine d`un nombre, trouvez l`« inverse » d`un carré. Le symbole de la racine carrée (√, également connu sous le nom de « signe radical ») est essentiellement le « opposé » du symbole carré (). Si vous voyez un signe radical, vous pouvez vous demander : « Quel nombre puis-je multiplier par lui-même pour obtenir le nombre sous le signe radical ??` Par exemple : si vous voyez la racine carrée (9), alors vous cherchez le nombre qui multiplié par lui-même a neuf comme produit. Dans ce cas c`est Trois, car 3 = 9.

3. Connaître la différence entre les carrés parfaits et imparfaits. Jusqu`à présent, les réponses aux problèmes de racine carrée étaient de jolis nombres ronds. Ce n`est pas toujours le cas - en fait, il existe des réponses aux racines carrées qui sont des nombres décimaux très longs et maladroits. Les nombres racines qui sont des nombres entiers (en d`autres termes, des nombres qui ne sont pas des fractions ou des nombres décimaux) sont appelés carrés. Tous les exemples ci-dessus (9, 25 et 64) sont des carrés (également appelés carrés parfaits), car en prenant des racines carrées, nous obtenons des nombres entiers (3, 5 et 8) en conséquence.

4. Mémorisez les 10-12 premiers carrés. Comme vous l`avez probablement remarqué, les racines carrées ou les carrés sont souvent très faciles! Parce que ces problèmes mathématiques sont si simples, cela vaut la peine d`apprendre les racines des 12 premiers carrés ou plus. Vous rencontrerez beaucoup ces nombres, vous pouvez donc gagner beaucoup de temps à long terme en les apprenant tôt. Les 12 premiers carrés sont :

5. Simplifiez les racines en supprimant les carrés lorsque cela est possible. Trouver les racines de carrés imparfaits peut parfois être délicat, surtout si vous n`utilisez pas de calculatrice (les paragraphes ci-dessous vous donnent des astuces pour faciliter ce processus). Cependant, il est souvent possible de simplifier les nombres sous le signe radical, pour faciliter le travail avec eux. Pour ce faire, il vous suffit de factoriser le nombre sous le radical, puis de prendre la racine carrée des facteurs qui sont des carrés, et d`écrire la réponse en dehors du radical. C`est plus facile qu`il n`y paraît - lisez la suite pour en savoir plus!

6. Utiliser des nombres imaginaires pour les racines de nombres négatifs. Quel carré est -16? Ce n`est pas 4 ou -4 - la quadrature des deux donne 16 (positif). Tu ne sais pas? En fait, il n`y a aucun moyen d`écrire la racine carrée de -16 ou tout nombre négatif avec des nombres réguliers. Dans ces cas, nous devons utiliser des nombres imaginaires (généralement sous la forme de lettres ou de symboles) pour remplacer la racine carrée du nombre négatif. Par exemple, la variable `i` est généralement utilisée pour la racine carrée de -1. En règle générale, la racine carrée d`un nombre négatif sera toujours un nombre imaginaire (ou en contiendra un).
Partie 2 sur 3: Utilisation d`algorithmes de division longue

1. Commandez votre problème de racine carrée comme une division longue. Bien que cela puisse prendre un peu de temps, il est possible de calculer les racines de carrés imparfaits difficiles sans calculatrice. Pour ce faire, nous utilisons une méthode de résolution (ou algorithme) qui est similaire à - mais pas exactement le même que - une longue division.
- Notez d`abord la racine carrée de la même manière que la division longue. Par exemple, disons que nous voulons calculer la racine carrée de 6,45, ce qui n`est certainement pas un carré parfait pratique. Nous écrivons d`abord un symbole radical ordinaire (√), puis nous écrivons le nombre en dessous. Ensuite, nous traçons une ligne au-dessus du nombre afin qu`il soit dans une petite "boîte" - tout comme une longue division. Lorsque nous avons terminé, nous avons noté un « √ » allongé avec 6,45 en dessous.
- Nous écrivons des nombres au-dessus du problème, alors laissez de l`espace.

2. Grouper les nombres par paires. Pour résoudre votre problème, regroupez les chiffres du nombre sous le signe radical par paires, en commençant par la virgule décimale. Vous pouvez ajouter de petits faits saillants (tels que des points, des barres obliques, des virgules, etc.) entre vos paires pour les différencier.

3. Trouvez le plus grand nombre dont le carré est inférieur ou égal au premier « groupe ». Commencez par le premier numéro ou la première paire sur la gauche. Choisissez le plus grand nombre avec un carré inférieur ou égal au « groupe ». Par exemple, si le groupe est de 37, vous choisiriez le 6, car 6 = 36 (moins de 37), mais 7 = 49 (supérieur à 37). Écrivez ce nombre au-dessus du premier groupe. Ceci est le premier chiffre de votre réponse.

4. Doublez le nombre que vous venez d`écrire, écrivez-le sous le premier groupe et soustrayez-le. Prenez le premier chiffre de votre réponse (le numéro que vous venez de trouver) et doublez-le. Écrivez-le sous votre premier groupe et soustrayez-le pour trouver la différence. Placez la prochaine paire de nombres à côté de la réponse ci-dessous. Enfin, écrivez le dernier chiffre du double du premier chiffre de votre réponse à gauche, en laissant un espace à côté.

5. Remplir l`espace vide. Ensuite, l`intention est d`ajouter un chiffre à droite du nombre que vous avez écrit à gauche. Choisissez un nombre qui multiplie par votre nouveau nombre produit le plus grand produit possible, mais est inférieur ou égal au nombre « tiré ». Par exemple, si votre nombre « tiré vers le bas » est 1700 et le nombre à gauche est 40_, vous devez remplir le blanc avec « 404 » car 404 × 4 = 1616 (moins de 1700), tandis que 405 × 5 = 2025. Le nombre que vous trouvez à cette étape est le deuxième chiffre de votre réponse, vous pouvez donc l`ajouter au-dessus du radical.

6. Continuez à utiliser vos numéros « vides » pour votre réponse. Continuez avec cette longue division modifiée jusqu`à ce que vous obteniez des zéros lorsque vous soustrayez le nombre de « tirer vers le bas », ou que vous ayez atteint la précision souhaitée. Lorsque vous avez terminé, les nombres que vous avez utilisés pour remplir les blancs à chaque étape (plus le tout premier nombre que vous avez utilisé) sont les chiffres de votre réponse.

sept. Déplacez la virgule décimale de votre "diviseur" d`origine vers le haut. Pour compléter votre réponse, vous devez mettre la virgule (le point décimal) au bon endroit. Heureusement, c`est facile - tout ce que vous avez à faire est de l`aligner avec la virgule décimale de votre numéro d`origine. Si le nombre sous le radical est 49,8, déplacez la virgule vers le haut entre les deux nombres au-dessus de 9 et 8.
Partie 3 sur 3: Estimer rapidement les carrés imparfaits

1. Trouver des carrés imparfaits en estimant. Une fois que vous avez mémorisé vos carrés, trouver les racines des carrés imparfaits devient beaucoup plus facile. Puisque vous connaissez déjà une douzaine de carrés, tout nombre qui se situe entre deux de ces carrés parfaits peut être trouvé en estimant entre ces valeurs. Pour commencer, trouvez les deux carrés entre lesquels votre nombre se situe. Déterminez ensuite lequel de ces deux carrés est le plus proche du nombre.
- Par exemple, supposons que nous ayons besoin de trouver la racine carrée de 40. Puisque nous avons mémorisé nos carrés, nous pouvons dire que 40 tombe entre 6 et 7, ou 36 et 49. Puisque 40 est supérieur à 6, sa racine carrée sera supérieure à 6, et puisqu`elle est inférieure à 7, sa racine carrée sera inférieure à 7. Le nombre 40 est un peu plus proche de 36 que 49, donc la réponse sera probablement un peu plus proche de 6. Dans les prochaines étapes, nous allons rendre notre réponse plus précise.

2. Estimer la racine carrée à une décimale près. Une fois que vous avez choisi deux carrés entre lesquels se trouve votre nombre, il ne vous reste plus qu`à estimer jusqu`à ce que vous trouviez une réponse qui vous satisfasse. Plus vous avancez, plus votre réponse est précise. Pour commencer, choisissez un dix pour votre réponse - il n`a pas besoin d`être correct, mais vous gagnerez du temps si vous faites preuve de bon sens en choisissant un nombre proche de la bonne réponse.

3. Multiplier l`estimation par elle-même. Ensuite, vous carré l`estimation. À moins que vous n`ayez de la chance, vous n`obtiendrez probablement pas votre numéro d`origine - vous finirez par être légèrement supérieur ou inférieur. Si votre réponse est trop élevée, réessayez avec une estimation légèrement inférieure (et vice versa si elle est trop faible).

4. Continuer l`estimation si nécessaire. Si vous êtes satisfait de vos réponses, vous voudrez peut-être simplement utiliser l`une de vos premières suppositions. Cependant, si vous voulez une réponse plus précise, tout ce que vous avez à faire est de choisir une estimation pour votre "centième" qui place cette estimation entre vos deux premières. Si vous continuez avec ce modèle, vous pouvez obtenir une réponse en trois, quatre décimales ou plus - cela dépend simplement de la distance que vous souhaitez parcourir.
Des astuces
- Pour des solutions rapides, utilisez une calculatrice. La plupart des calculatrices modernes peuvent calculer directement les racines carrées. Habituellement, il vous suffit de saisir votre numéro puis d`appuyer sur le bouton avec le radical de la seconde puissance (la racine carrée). Par exemple, pour trouver la racine carrée de 841, appuyez sur les touches suivantes : 8, 4, 1, (√) et faites-le correctement 29 sur comme réponse.
Articles sur le sujet "Résoudre les racines carrées"
Оцените, пожалуйста статью
Populaire