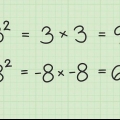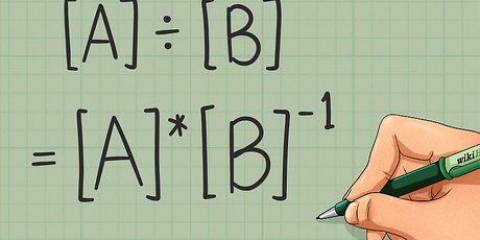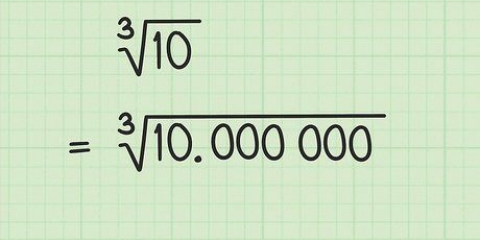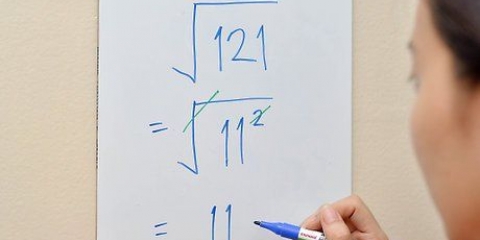Division des racines carrées

Teneur

Pas
Des astuces
Mises en garde

Diviser par des racines carrées est essentiellement la simplification d`une fraction. Bien sûr, la présence de racines carrées rend le processus un peu plus compliqué, mais il existe des règles qui nous permettent de travailler avec des fractions de manière relativement simple. La chose la plus importante à retenir est que vous devez diviser les coefficients par les coefficients et les racines par les racines. Vous ne devez également jamais laisser de racine carrée dans un dénominateur.

Pas

Méthode 1 sur 4: Partager des carottes

Image intitulée Diviser les racines carrées Étape 1

1. Mettre en place la fraction. Si l`expression n`est pas déjà sous la forme d`une fraction, réécrivez-la comme ceci. Cela permet de suivre plus facilement toutes les étapes nécessaires pour diviser par une racine carrée. N`oubliez pas qu`un caractère de division est identique à une barre de fraction.

Par exemple, si vous $\sqrt{144} ?? \sqrt{36}$ ${sqrt{144}}div {sqrt{36}}$ calcule, puis réécrivez le problème comme suit : $\frac{\sqrt{144}}{\sqrt{36}}$ ${frac{{sqrt{144}}}{{sqrt{36}}}}$ .

Image intitulée Diviser les racines carrées, étape 2

2. Utiliser un signe radical. Si votre problème a une racine carrée au numérateur et au dénominateur, vous pouvez placer les deux racines sous un radical. (Une racine est le nombre sous le radical.) Cela rend la simplification encore plus facile.

Par exemple,

\frac{\sqrt{144}}{\sqrt{36}}

${frac{{sqrt{144}}}{{sqrt{36}}}}$ peut être réécrit comme

\sqrt{\frac{144}{36}}

${sqrt{{frac{144}{36}}}}$ .

Image intitulée Diviser les racines carrées, étape 3

3. Diviser les racines. Divisez les nombres comme vous le feriez avec n`importe quel entier. Assurez-vous de placer le quotient sous un nouveau radical.

Par exemple,

\frac{144}{36} = 4

${frac{144}{36}}=4$ , Alors

\sqrt{\frac{144}{36}} = \sqrt{4}

${sqrt{{frac{144}{36}}}}={sqrt{4}}$ .

Image intitulée Diviser les racines carrées, étape 4

4. Simplifier, Si nécessaire. Si la racine est un carré, ou si l`un des facteurs est un carré parfait, alors vous devez simplifier l`expression. Un carré ou carré parfait est le produit d`un nombre entier multiplié par lui-même. Par exemple, 25 est un carré parfait car

5 \times 5 = 25

$5fois 5=25$ .

Par exemple, 4 est un carré parfait car

2 \times 2 = 4

$2fois 2=4$ . Ainsi:

\sqrt{4}

${sqrt{4}}$

= \sqrt{2 \times 2}

$={sqrt{2fois 2}}$

= 2

$=2$
alors,

\frac{\sqrt{144}}{\sqrt{36}} = \sqrt{4} = 2

${frac{{sqrt{144}}}{{sqrt{36}}}}={sqrt{4}}=2$ .

Méthode 2 sur 4: Factoriser les racines

Image intitulée Diviser les racines carrées Étape 5

1. Exprimer le problème sous forme de fraction. L`expression est probablement déjà écrite de cette façon. Si non, changez-le. En faire une fraction rend les étapes nécessaires plus faciles à suivre, en particulier lors de la factorisation des racines carrées. N`oubliez pas qu`un caractère de division est identique à une barre de fraction.

Par exemple, lors du calcul $\sqrt{8} ?? \sqrt{36}$ ${sqrt{8}}div {sqrt{36}}$ , réécrivez l`expression sous la forme : $\frac{\sqrt{8}}{\sqrt{36}}$ ${frac{{sqrt{8}}}{{sqrt{36}}}}$ .

Image intitulée Divide Square Roots Step 6

2. Factoriser chaque carotte en facteurs. Factorisez le nombre comme vous le feriez avec un nombre entier. Laisser les facteurs sous les signes radicaux.

Par exemple:

\frac{\sqrt{8}}{\sqrt{36}} = \frac{\sqrt{2 \times 2 \times 2}}{\sqrt{6 \times 6}}

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{{sqrt{2times 2times 2}}}{{sqrt{6times 6 }}}}$

Image intitulée Divide Square Roots Step 7

3. Simplifier le numérateur et le dénominateur de la fraction. À pour simplifier une racine carrée, excluez-vous tous les facteurs dont le produit est un carré ?. Un carré est le résultat d`un nombre entier multiplié par lui-même. Le facteur devient maintenant un coefficient en dehors de la racine carrée.

Par exemple:

\sqrt{} 2 \times 2 \times 2 \sqrt{6 \times 6}

${frac{{sqrt{{cancel{2times 2times }}2}}}{{sqrt{{cancel{6times 6}}}}}}}$

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$
alors,

\frac{\sqrt{8}}{\sqrt{36}} = 2 \sqrt{2} 6

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{2{sqrt{2}}}{6}}$

Image intitulée Divide Square Roots Step 8

4. Éliminer le signe radical du dénominateur, si nécessaire. En règle générale, une expression ne peut pas avoir de racine carrée au dénominateur. Si votre fraction a une racine carrée au dénominateur, vous devez l`éliminer. Cela signifie supprimer la racine dans le dénominateur. Pour ce faire, multipliez le numérateur et le dénominateur de la fraction par la racine carrée dont vous avez besoin pour éliminer.

Par exemple, supposons que votre expression est

6 \sqrt{2} \sqrt{3}

${frac{6{sqrt{2}}}{{sqrt{3}}}}$ , alors vous devez multiplier le numérateur et le dénominateur par

\sqrt{3}

${sqrt{3}}$ pour supprimer la racine carrée du dénominateur :

6 \sqrt{2} \sqrt{3} \times \frac{\sqrt{3}}{\sqrt{3}}

${frac{6{sqrt{2}}}{{sqrt{3}}}}times {frac{{sqrt{3}}}{{sqrt{3}}}}$

= 6 \sqrt{2} \times \sqrt{3} \sqrt{3} \times \sqrt{3}

$={frac{6{sqrt{2}}times {sqrt{3}}}{{sqrt{3}}times {sqrt{3}}}}$

= 6 \sqrt{6} \sqrt{9}

$={frac{6{sqrt{6}}}{{sqrt{9}}}}$

= 6 \sqrt{6} 3

$={frac{6{sqrt{6}}}{3}}$ .

Image intitulée Divide Square Roots Step 9

5. Simplifier davantage, si nécessaire. Parfois, vous vous retrouvez avec des coefficients qui peuvent être encore simplifiés, ou réduire. Simplifiez les nombres entiers dans le numérateur et le dénominateur comme vous le feriez pour une fraction.

Par exemple,

\frac{2}{6}

${frac{2}{6}}$ peut être réduit à

\frac{1}{3}

${frac{1}{3}}$ , Alors

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$ peut être réduit à

1 \sqrt{2} 3

${frac{1{sqrt{2}}}{3}}$ , ou simplement

\frac{\sqrt{2}}{3}

${frac{{sqrt{2}}}{3}}$ .

Méthode 3 sur 4: Division des racines carrées avec des coefficients

Image intitulée Diviser les racines carrées Étape 10

1. Simplifier les coefficients. Ce sont les nombres en dehors du radical. Pour les simplifier, partagez ou réduire, ignorer les racines carrées pour l`instant.

Par exemple, si vous $4 \sqrt{32} 6 \sqrt{16}$ ${frac{4{sqrt{32}}}{6{sqrt{16}}}}$ devez calculer, puis vous simplifiez d`abord $\frac{4}{6}$ ${frac{4}{6}}$ . Le numérateur et le dénominateur peuvent tous deux être divisés par un facteur de 2. Vous pouvez donc simplifier cela en : $\frac{4}{6} = \frac{2}{3}$ ${frac{4}{6}}={frac{2}{3}}$ .

Image intitulée Divide Square Roots Step 11

2. Simplifier les racines carrées. Si le numérateur est divisible par le dénominateur, il suffit de diviser les nombres sous les radicaux. Sinon, simplifiez chaque racine carrée de la même manière que les autres racines carrées.

Par exemple, puisque 32 est divisible par 16, vous pouvez diviser les racines carrées :

\sqrt{\frac{32}{16}} = \sqrt{2}

${sqrt{{frac{32}{16}}}}={sqrt{2}}$ .

Image intitulée Divide Square Roots Step 12

3. Multiplier le(s) coefficient(s) simplifié(s) par la racine carrée simplifiée. Rappelez-vous qu`il ne peut pas y avoir de racine carrée dans un dénominateur, donc lorsque vous multipliez une fraction par une racine carrée, vous mettez la racine carrée dans le numérateur.

Par exemple,

\frac{2}{3} \times \sqrt{2} = 2 \sqrt{2} 3

${frac{2}{3}}times {sqrt{2}}={frac{2{sqrt{2}}}{3}}$ .

Image intitulée Divide Square Roots Step 13

4. Éliminer la racine carrée au dénominateur, si nécessaire. C`est ce qu`on appelle la rationalisation du dénominateur. La règle est qu`une expression ne peut pas avoir de racine carrée au dénominateur. Pour soustraire la racine du dénominateur, multipliez le numérateur et le dénominateur par la racine carrée que vous souhaitez soustraire.

Par exemple, si vous avez une expression comme

4 \sqrt{3} 2 \sqrt{sept}

${frac{4{sqrt{3}}}{2{sqrt{7}}}}$ , alors vous devez multiplier le numérateur et le dénominateur par

\sqrt{sept}

${sqrt{7}}$ pour éliminer la racine carrée au dénominateur :

4 \sqrt{3} \sqrt{sept} \times \frac{\sqrt{sept}}{\sqrt{sept}}

${frac{4{sqrt{3}}}{{sqrt{7}}}}times {frac{{sqrt{7}}}{{sqrt{7}}}}$

= 4 \sqrt{3} \times \sqrt{sept} \sqrt{sept} \times \sqrt{sept}

$={frac{4{sqrt{3}}times {sqrt{7}}}{{sqrt{7}}times {sqrt{7}}}}$

= 4 \sqrt{21} \sqrt{49}

$={frac{4{sqrt{21}}}{{sqrt{49}}}}$

= 4 \sqrt{21} sept

$={frac{4{sqrt{21}}}{7}}$

Méthode 4 sur 4: Division par un binôme avec une racine carrée

Image intitulée Divide Square Roots Step 14

1. Déterminez si vous avez un binôme au dénominateur. Le dénominateur est le nombre dans le problème que vous divisez par. Un binôme est un polynôme à deux termes. Cette méthode ne s`applique qu`à la division des racines carrées impliquant un binôme.

Par exemple, si vous $1 5 + \sqrt{2}$ ${frac{1}{5+{sqrt{2}}}}$ Si vous voulez calculer, vous avez un binôme au dénominateur, car $5 + \sqrt{2}$ $5+{sqrt{2}}$ est un polynôme à deux termes.

Image intitulée Divide Square Roots Step 15

2. Déterminer la conjonction du binôme. Les paires conjuguées sont des binômes avec les mêmes termes mais des opérateurs opposés. En utilisant une paire de subjonctifs, vous pouvez éliminer la racine carrée du dénominateur.

Par exemple,

5 + \sqrt{2}

$5+{sqrt{2}}$ et

5 - \sqrt{2}

$5-{sqrt{2}}$ sont des paires conjonctives, car elles ont les mêmes termes, mais des opérateurs opposés.

Image intitulée Divide Square Roots Step 16

3. Multiplier le numérateur et le dénominateur par la conjonction du dénominateur. Cela vous permet d`éliminer la racine carrée, car le produit d`une paire conjuguée est la différence du carré de chaque terme du binôme. C`est-à-dire,

(une - b) (une + b) = une 2 - b^{2}

$(a-b)(a+b)=a^{{2}}-b^{{2}}$ .

Par exemple:

1 5 + \sqrt{2}

${frac{1}{5+{sqrt{2}}}}$

= 1 (5 - \sqrt{2}) (5 + \sqrt{2}) (5 - \sqrt{2})

$={frac{1(5-{sqrt{2}})}{(5+{sqrt{2}})(5-{sqrt{2}})}}$

= 5 - \sqrt{2} (5 2 - (\sqrt{2})^{2}

$={frac{5-{sqrt{2}}}{(5^{{2}}-({sqrt{2}})^{{2}}}}$

= 5 + \sqrt{2} 25 - 2

$={frac{5+{sqrt{2}}}{25-2}}$

= 5 + \sqrt{2} 23

$={frac{5+{sqrt{2}}}{23}}$
Donc,

1 5 + \sqrt{2} = 5 + \sqrt{2} 23

${frac{1}{5+{sqrt{2}}}}={frac{5+{sqrt{2}}}{23}}$ .

Des astuces

De nombreuses calculatrices ont des fonctions spéciales pour les fractions. Entrez le coefficient du numérateur, appuyez sur le bouton des fractions, puis entrez le coefficient du dénominateur. Lorsque vous appuyez sur le signe égal par la suite, la calculatrice devrait avoir réécrit les coefficients dans les plus petits termes.
Contrairement à l`addition et à la soustraction de racines, dans une fraction, il n`est pas nécessaire de simplifier d`abord les racines pour supprimer les carrés. En fait, il est souvent préférable de ne pas le faire.
Si vous travaillez avec des racines carrées, les fractions impropres sont plus faciles à résoudre que les nombres fractionnaires.

Mises en garde

Ne jamais mettre un nombre décimal dans une fraction. Ce serait autrement une fraction dans une fraction.
Ne jamais ajouter un nombre décimal ou mixte à une racine, le convertir en fraction et simplifier l`expression entière.
Ne jamais laisser de racine carrée dans le dénominateur d`une fraction, mais simplifier la fraction.
Si le dénominateur contient une forme d`addition ou de soustraction, utilisez la méthode des paires conjuguées pour supprimer le radical du dénominateur.