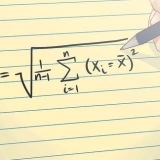Calcul de la covariance

Teneur

Pas
Mises en garde

La covariance est un calcul statistique pour rendre la relation entre deux ensembles de données plus transparente. Supposons, par exemple, que les anthropologues étudient la taille et le poids d`une population au sein d`une culture particulière. Pour chaque personne dans l`étude, la taille et le poids peuvent être représentés avec une paire de données (x, y). Ces valeurs peuvent être utilisées dans une formule standard pour calculer la relation de covariance. Cet article explique d`abord les calculs pour déterminer la covariance d`un ensemble de données. Ensuite, deux autres manières automatisées de déterminer le résultat seront discutées.

Pas

Méthode 1 sur 4: Calculer la covariance à la main à l`aide de la formule standard

Image intitulée Calculer la covariance étape 1

1. Apprenez la formule de covariance standard et ses parties. La formule standard pour calculer la covariance est

?? (X je - X_{moyenne}) ({oui}_{je} - {oui}_{moyenne}) / (m - 1)

$Sigma (x_{i}-x_{{text{moy}}})(y_{i}-y_{{text{moy}}})/(n-1)$ . Pour utiliser cette formule, vous devez connaître la signification des variables et des symboles :

$??$ $Sigma$ - Ce symbole est la lettre grecque `sigma`. Dans les fonctions mathématiques, cela signifie ajouter une série de ce qui suit. Dans cette formule, le signe signifie que vous calculez les valeurs au numérateur de la fraction, puis les additionnez toutes ensemble, puis divisez le total par le dénominateur.
$X je$ $x_{i}$ - Vous pouvez lire cette variable comme `x sub i`. L`indice i représente un compteur. Cela signifie que vous allez faire un calcul pour chaque valeur de x dans votre ensemble de données.
$X une v g$ $x_{{moy}}$ - Le `moy` indique que x(avg) est la valeur moyenne de tous les points de données x. La moyenne est parfois écrite sous la forme d`un x avec une courte ligne horizontale au-dessus. Dans ce style, vous lisez la variable comme `x-bar`, mais cela signifie toujours la moyenne de l`ensemble de données.
$oui je$ $y_{i}$ - Vous pouvez lire cette variable comme `y sub i`. L`indice i est le numérateur. Cela signifie que vous allez faire un calcul pour chaque valeur de y dans votre ensemble de données.
$oui une v g$ $y_{{moy}}$ - Le `moy` indique que y(avg) est la valeur moyenne de tous les points de données x. La moyenne est parfois écrite sous la forme d`un y avec une courte ligne horizontale au-dessus. Dans ce style, vous lisez la variable comme "y-bar", mais cela signifie toujours la moyenne de l`ensemble de données.
$m$ $m$ - Cette variable est le nombre d`éléments dans votre jeu de données. Rappelez-vous que dans un problème de covariance, un seul "élément" est composé à la fois d`une valeur x et d`une valeur y. La valeur « n » est le nombre de paires de points de données, pas de nombres individuels.

Image intitulée Calculer la covariance, étape 2

2. Construisez votre table de données. Avant de se lancer, il est utile de collecter vos données. Créer un tableau avec cinq colonnes. Vous devez déclarer chaque colonne comme suit :

X

$X$ - Remplissez cette colonne avec les valeurs des points des données x.

oui

$oui$ - Remplissez cette colonne avec les valeurs des données y. Assurez-vous que les valeurs y sont alignées avec les valeurs x correspondantes. Dans un problème de covariance, l`ordre des points de données et le couplage de x et y sont importants.

(X je - X_{moyenne})

$(x_{i}-x_{{text{avg}}})$ - Laissez cette colonne vide au début. Vous allez le remplir de données après avoir fait la moyenne des données x.

(oui je - {oui}_{moyenne})

$(y_{i}-y_{{text{avg}}})$ - Laissez cette colonne vide au début. Vous allez le remplir de données après avoir fait la moyenne des données y.

Produit

${text{Produit}}$ - Laissez la dernière colonne vide aussi. Celui-ci sera rempli lors du traitement de la mission.

Image intitulée Calculer la covariance, étape 3

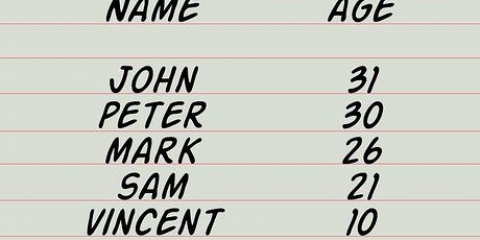
3. Calculer la moyenne des x points de données. Cet exemple de collecte de données contient 9 nombres. Pour trouver la moyenne, additionnez-les et divisez la somme par 9. Cela donne le résultat 1 + 3 + 2 + 5 + 8 + 7 + 12 + 2 + 4 = 44. Lorsque vous divisez cela par 9, vous obtenez la moyenne 4,89. C`est la valeur que vous utiliserez comme x(moy) pour les calculs à venir.

Image intitulée Calculer la covariance, étape 4

4. Calculer la moyenne des points de données y. Cette colonne y doit également comprendre 9 points de données qui coïncident avec les points de données x. Déterminer la moyenne de ce. Pour cet exemple d`ensemble de données, cela devient 8 + 6 + 9 + 4 + 3 + 3 + 2 + 7 + 7 = 49. Divisez ce total par 9 pour obtenir une moyenne de 5,44. Vous allez utiliser 5,44 comme valeur de y(avg) pour les calculs à venir.

Image intitulée Calculer la covariance étape 5

5. Calculer les valeurs (Xje-Xmoyenne){style d`affichage (x_{i}-x_{text{avg}})} $(x_{i}-x_{{text{avg}}})$ . Pour chaque élément de la colonne x, calculez la différence entre ce nombre et la valeur moyenne. Pour cet exemple de problème, cela signifie soustraire 4,89 de chaque valeur x. Si le point de données d`origine est inférieur à la moyenne, votre résultat sera négatif. Si le point de données d`origine est supérieur à la moyenne, le résultat sera positif. Assurez-vous de garder une trace des valeurs négatives.

Par exemple, le premier point de données dans la colonne x est 1. La valeur à saisir sur la première ligne de la colonne

(X je - X_{moyenne})

$(x_{i}-x_{{text{avg}}})$ est : 1 – 4,89 = -3,89.

Répétez ce processus pour chaque point de données. Donc la deuxième ligne devient : 3 - 4,89 = -1.89. La troisième ligne devient : 2 - 4,89 = -2,89. Continuer ce processus pour tous les points de données. Les neuf nombres de cette colonne deviennent : -3,89, -1,89, -2,89, 0,11, 3,11, 2,11, 7.11, -2,89, -0,89.

Image intitulée Calculer la covariance, étape 6

6. Calculer les valeurs (ouije-ouimoyenne){style d`affichage (y_{i}-y_{text{avg}})} $(y_{i}-y_{{text{avg}}})$ . Dans cette colonne, vous allez faire des soustractions similaires, en utilisant les points de données y et la moyenne y. Si le point de données d`origine est inférieur à la moyenne, le résultat sera négatif. Si le point de données d`origine est supérieur à la moyenne, alors votre résultat sera positif. Assurez-vous de garder une trace des valeurs négatives.

Donc pour la première ligne votre calcul sera : 8 -5,44, = 2,56.

La deuxième ligne devient : 6 – 5,44 = 0,56.

Continuez à soustraire les valeurs jusqu`à la fin de la liste de données. Lorsque vous avez terminé, vous devriez avoir les neuf valeurs suivantes dans cette colonne : 2,56, 0,56, 3,56, -1,44, -2,44, -2,44, -3,44 , 1,56, 1,56.

Image intitulée Calculer la covariance étape 7

sept. Calculer les produits pour chaque ligne de données. Vous remplissez les lignes de la dernière colonne en multipliant les nombres que vous avez calculés dans les deux colonnes précédentes de

(X je - X_{moyenne})

$(x_{i}-x_{{text{avg}}})$ et

(oui je - {oui}_{moyenne})

$(y_{i}-y_{{text{avg}}})$ . Travaillez à votre guise ligne par ligne, en multipliant les deux nombres par leurs points de données correspondants. Méfiez-vous des valeurs négatives en cours de route.

Dans la première ligne de cet exemple de données, le

(X je - X_{moyenne})

$(x_{i}-x_{{text{avg}}})$ vous avez calculé -3,89, et le

(oui je - {oui}_{moyenne})

$(y_{i}-y_{{text{avg}}})$ valeur 2,56. Le produit de ces deux nombres est : -3,89 x 2,56 = -9,96.

Pour la deuxième ligne, multipliez les deux nombres : -1,88 x 0,56 = -1,06.

Continuez à multiplier ligne par ligne jusqu`à la fin de l`ensemble de données. Lorsque vous avez terminé, les neuf valeurs de cette colonne doivent indiquer : -9,96, -1,06, -10,29, -0,16, -7,59, -5,15, -24,46 , -4,51, -1,39.

Image intitulée Calculer la covariance, étape 8

8. Trouvez la somme des valeurs dans la dernière colonne. C`est ici qu`intervient le symbole. Après avoir fait tous les calculs jusqu`à présent, additionnez les résultats. Pour cet exemple d`ensemble de données, vous devriez maintenant avoir neuf valeurs dans la dernière colonne. Additionnez ces neuf nombres ensemble. Faites très attention à savoir si un nombre est positif ou négatif.

La somme de cet exemple d`ensemble de données doit totaliser -64,57. Écrivez ce total dans l`espace au bas de la colonne. C`est la valeur du numérateur de la formule de covariance standard.

Image intitulée Calculer la covariance étape 9

9. Calculer le dénominateur de la formule de covariance. Le numérateur de la formule de covariance standard est la valeur que vous venez de calculer. Le dénominateur est représenté par (n-1), et est un de moins que le nombre de paires de données dans votre ensemble de données.

Dans cet exemple de problème, il y a neuf paires de données, donc n vaut 9. Par conséquent, la valeur de (n-1) est égale à 8.

Image intitulée Calculer la covariance étape 10

dix. Diviser le numérateur par le dénominateur. La dernière étape du calcul de la covariance consiste à diviser le numérateur,

?? (X je - X_{moyenne}) ({oui}_{je} - {oui}_{moyenne})

$Sigma (x_{i}-x_{{text{avg}}})(y_{i}-y_{{text{avg}}})$ par le dénominateur,

(m - 1)

$(n-1)$ . Le quotient est la covariance de vos données.

Pour cet exemple d`ensemble de données, ce calcul est : -64,57/8 = -8,07.

Méthode 2 sur 4: Calculer la covariance à l`aide d`une feuille de calcul Excel

Image intitulée Calculer la covariance étape 11

1. Remarquez quels sont les calculs répétitifs. La covariance est un calcul que vous devez faire à la main plusieurs fois pour comprendre le sens du résultat. Cependant, si vous utilisez régulièrement la covariance pour interpréter les données, vous avez besoin d`un moyen plus rapide et automatisé d`obtenir les résultats. Vous avez peut-être déjà remarqué qu`avec notre ensemble de données relativement petit de seulement neuf paires de données, les calculs consistaient en deux moyennes, dix-huit soustractions distinctes, neuf multiplications, une addition et enfin une autre division. C`est 31 calculs relativement petits pour trouver la solution. En cours de route, vous courez le risque de manquer des signes négatifs ou de copier les résultats de manière incorrecte, ce qui rend la réponse incorrecte.

Image intitulée Calculer la covariance étape 12

2. Créer une feuille de calcul pour calculer la covariance. Si vous êtes familier avec Excel (ou tout autre programme de calcul), vous pouvez facilement créer un tableau pour déterminer la covariance. Étiquetez les en-têtes des cinq colonnes comme dans les calculs manuels : x, y, (x(i)-x(avg)), (y(i)-y(avg)) et Product.

Pour simplifier le nommage, nommez la troisième colonne quelque chose comme "x différence" et la quatrième colonne "y différence", tant que vous vous souvenez de la signification des données.

Si le tableau commence dans le coin supérieur gauche de la feuille de calcul, la cellule A1 sera étiquetée x, tandis que les autres étiquettes continueront à la cellule E1.

Image intitulée Calculer la covariance étape 13

3. Remplissez les points de données. Tapez les valeurs des données dans les deux colonnes x et y. N`oubliez pas que l`ordre des points de données est important, vous devez donc faire correspondre chaque y avec la valeur correspondante de x.

Les valeurs x commencent dans la cellule A2 et continuent jusqu`au nombre de points de données dont vous avez besoin.

Les valeurs y commencent dans la cellule B2 et continuent jusqu`au nombre de points de données dont vous avez besoin.

Image intitulée Calculer la covariance, étape 14

4. Déterminer les moyennes des valeurs x et y. Excel calcule les moyennes pour vous très rapidement. Dans la première cellule vide sous chaque colonne de données, tapez la formule =AVERAGE(A2:A___). Remplissez le blanc avec le numéro de la cellule qui correspond à votre dernier point de données.

Par exemple, si vous avez 100 points de données, les cellules A2 à A101 seront remplies, donc dans la cellule vous taperez : = MOYENNE(A2:A101).

Pour les données y, tapez la formule = MOYENNE(B2:B101).

N`oubliez pas qu`une formule dans Excel commence par un signe `=`.

Image intitulée Calculer la covariance, étape 15

5. Tapez la formule pour la colonne (x(i)-x(avg)). Dans la cellule C2, entrez la formule de calcul de la première soustraction. Cette formule devient : =A2-___. Remplissez l`espace vide avec l`adresse de la cellule qui contient la moyenne des données x.

Par exemple, les 100 points de données sont moyennés dans la cellule A103, votre formule devient donc : =A2-A103.

Image intitulée Calculer la covariance, étape 16

6. Répétez la formule pour les points de données (y(i)-y(avg)). En suivant le même exemple ce sera dans la cellule D2. La formule devient : =B2-B103.

Image intitulée Calculer la covariance étape 17

sept. Tapez la formule pour la colonne "Produit". Dans la cinquième colonne, vous devez taper dans la cellule E2 la formule de calcul du produit des deux cellules précédentes. Cela devient alors : =C2*D2.

Image intitulée Calculer la covariance étape 18

8. Copiez les formules pour remplir le tableau. Jusqu`à présent, vous n`avez programmé que les premiers points de données de la ligne 2. À l`aide de votre souris, mettez en surbrillance les cellules C2, D2 et E2. Placez votre curseur sur la petite case dans le coin inférieur droit jusqu`à ce qu`un signe plus apparaisse. Cliquez et maintenez le bouton de la souris et faites glisser la souris vers le bas pour étendre la sélection et remplir l`intégralité du tableau de données. Cette étape copiera automatiquement les trois formules des cellules C2, D2 et E2 dans l`ensemble du tableau. Le tableau doit être automatiquement rempli avec tous les calculs.

Image intitulée Calculer la covariance étape 19

9. Programmer la somme de la dernière colonne. Vous avez besoin de la somme des éléments dans la colonne « Produit ». Dans la cellule vide immédiatement en dessous du dernier point de données de cette colonne, tapez la formule : =SUM(E2:E___). Remplissez le blanc avec l`adresse de la cellule du dernier point de données.

Dans l`exemple avec 100 points de données, cette formule va dans la cellule E103. Tapez : =SOMME(E2 :E102).

Image intitulée Calculer la covariance étape 20

dix. Déterminer la covariance. Vous pouvez également laisser Excel faire le calcul final pour vous. Le dernier calcul de la cellule E103 dans notre exemple représente le numérateur de la formule de covariance. Immédiatement en dessous de cette cellule, tapez la formule : =E103/___. Remplissez le blanc avec le nombre de points de données que vous avez. Dans notre exemple, c`est 100. Le résultat est la covariance de vos données.

Méthode 3 sur 4: Utilisation de calculateurs de covariance en ligne

Image intitulée Calculer la covariance étape 21

1. Rechercher en ligne des calculateurs de covariance. Diverses écoles, entreprises ou autres sources ont des sites Web qui calculent les valeurs de covariance très facilement pour vous. Utilisez le terme de recherche « calculateur de covariance » dans un moteur de recherche.

Image intitulée Calculer la covariance étape 22

2. Entrez vos coordonnées. Veuillez lire attentivement les instructions sur le site Web pour vous assurer de saisir correctement les informations. Il est important que vos paires de données soient conservées dans l`ordre, sinon le résultat généré sera une covariance incorrecte. Les sites Web ont des styles de saisie de données différents.

Sur le site Internet http://ncalculateurs.com/statistics/covariance-calculator.htm, par exemple y a-t-il une case horizontale pour saisir les valeurs x et une deuxième case horizontale pour saisir les valeurs y. Vous devez saisir vos données séparées par des virgules. Ainsi, l`ensemble de données x calculé plus tôt dans cet article doit alors être entré comme 1,3,2,5,8,7,12,2,4. Les données y comme 8,6,9,4,3,3,2,7,7.

Sur un autre site, https://www.la calculatrice.co/math/Covariance-Calculatrice-705.html, il vous sera demandé d`entrer les données x dans la première case. Les données sont saisies verticalement, avec un élément par ligne. Par conséquent, l`entrée sur ce site ressemble à :

sept

Image intitulée Calculer la covariance, étape 23

3. Calculez vos résultats. La chose intéressante à propos de ces calculs en ligne est qu`après avoir entré les données, vous n`avez généralement qu`à cliquer sur le bouton "Calculer", après quoi les résultats apparaissent automatiquement. La plupart des sites vous fourniront les calculs intermédiaires de x(avg), y(avg) et n.

Méthode 4 sur 4: Interprétation des résultats de la covariance

Image intitulée Calculer la covariance, étape 24

1. Rechercher une relation positive ou négative. La covariance est un nombre statistique unique qui indique la relation entre un ensemble de données et un autre. Dans l`exemple mentionné dans l`introduction, la taille et le poids sont mesurés. Vous vous attendriez à ce qu`au fur et à mesure que les gens grandissent, leur poids augmentera également, conduisant à une vue de covariance positive. Autre exemple : supposons que des données soient collectées indiquant le nombre d`heures qu`une personne a pratiqué le golf et le score qu`elle obtient. Dans ce cas, vous vous attendez à une covariance négative, ce qui signifie qu`à mesure que le nombre d`heures d`entraînement augmente, le score de golf diminuera. (Au golf, un score inférieur est meilleur).

Considérez l`ensemble de données d`échantillon calculé ci-dessus. La covariance résultante est de -8,07. Le signe moins signifie qu`à mesure que les valeurs x augmentent, les valeurs y ont tendance à diminuer. Vous pouvez voir que cela est vrai en regardant certaines des valeurs. Par exemple, les valeurs x de 1 et 2 correspondent aux valeurs y de 7, 8 et 9. Les valeurs x de 8 et 12 sont liées aux valeurs y de 3 et 2. respectivement.

Image intitulée Calculer la covariance, étape 25

2. Interpréter la taille de la covariance. Si le nombre du score de covariance est grand, qu`il s`agisse d`un grand nombre positif ou d`un grand nombre négatif, vous pouvez interpréter cela comme deux éléments de données fortement connectés, de manière positive ou négative.

La covariance -8,07 de l`ensemble de données de l`échantillon est assez grande. Notez que les données vont de 1 à 12. Donc 8 est un nombre assez grand. Cela indique une relation assez forte entre les ensembles de données x et y.

Image intitulée Calculer la covariance, étape 26

3. Comprendre l`absence de relation. Si votre résultat est une covariance égale ou très proche de 0, alors vous pouvez conclure que les points de données n`ont aucune relation. Autrement dit, une augmentation d`une valeur peut, mais ne doit pas nécessairement conduire à une augmentation de l`autre. Les deux termes sont liés presque arbitrairement.

Supposons que vous associez les tailles de chaussures aux notes d`examen. Parce qu`il y a tellement de facteurs qui affectent les notes d`examen d`un étudiant, un score de covariance proche de 0 est à prévoir. Cela indique qu`il n`y a presque pas de relation entre les deux valeurs.

Image intitulée Calculer la covariance étape 27

4. Visualiser la relation graphiquement. Pour comprendre visuellement la covariance, vous pouvez tracer vos points de données dans un graphique x,y. Lorsque vous faites cela, vous devriez voir assez facilement que les points, bien qu`ils ne soient pas exactement en ligne droite, ont tendance à s`approcher d`un groupe en diagonale du haut à gauche vers le bas à droite. Ceci est la description d`une covariance négative. Vous voyez également que la valeur de la covariance est de -8,07. C`est un nombre assez important par rapport aux points de données. Le nombre élevé suggère que la covariance est assez forte, ce qui peut être déduit de la forme linéaire des points de données.

Pour revoir cela à nouveau, lisez les articles de wikiHow sur le dessin de points dans un système de coordonnées.

Mises en garde

La covariance a une application limitée dans les statistiques. C`est souvent une étape vers le calcul de coefficients de corrélation ou d`autres concepts. Attention aux interprétations trop audacieuses basées sur un score de covariance.