Dans l`exemple ci-dessus, cela ressemblerait à ceci : 
Dans l`exemple ci-dessus, vous calculez ceci comme suit :
Cette équation vous donne l`écart total au carré des lectures par rapport à la moyenne de l`échantillon. Notez que le signe de la différence n`a pas d`importance. 
Dans l`exemple ci-dessus, vous avez 5 lectures, donc n – 1 = 4. Votre calcul ressemble à ceci : 
Dans l`exemple ci-dessus, vous calculez l`écart type comme suit :
L`écart type est donc de 0,0071624. 
Calcul de l'erreur standard
Teneur
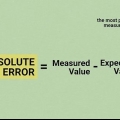
« Erreur-type » fait référence à l`écart-type de la distribution d`échantillonnage des données statistiques. En d`autres termes, cela peut être utilisé pour calculer la précision d`une moyenne d`échantillon. Dans de nombreux cas, lors de l`utilisation de l`erreur standard, une distribution normale est implicitement supposée. Si vous souhaitez calculer l`erreur standard, lisez la suite à l`étape 1.
Pas
Partie1 sur 3: Les bases

1. L`écart type. L`écart type d`un échantillon indique le degré d`étalement des nombres. L`écart type d`un échantillon est généralement indiqué par un s. La formule mathématique de l`écart type est indiquée ci-dessus.

2. La population moyenne. La moyenne de la population est la moyenne d`un ensemble de données numériques qui contient toutes les valeurs de l`ensemble du groupe - en d`autres termes, la moyenne d`un ensemble complet de nombres, plutôt que d`un échantillon.

3. La moyenne arithmétique. Ceci n`est qu`une moyenne : la somme d`un certain nombre de valeurs, divisée par ce même nombre de valeurs.

4. Reconnaître les moyennes de l`échantillon. Lorsqu`une moyenne arithmétique est basée sur une série d`observations obtenues par échantillonnage d`une population statistique, elle est appelée « moyenne d`échantillon.” Il s`agit de la moyenne d`un ensemble numérique de données dans lequel certaines des valeurs d`un groupe sont contenues. On l`appelle :

5. La distribution normale. La distribution normale, la plus couramment utilisée de toutes les distributions, est symétrique, avec une valeur aberrante à la moyenne des données. La forme du graphique est celle d`une horloge, la pente étant égale de part et d`autre du sommet. Cinquante pour cent de la distribution est à gauche et cinquante pour cent à droite. La distribution d`une distribution normale est déterminée par l`écart type.

6. La formule standard. La formule pour l`erreur standard d`une moyenne d`échantillon est donnée ci-dessus.
Partie 2 sur 3: Calcul de l`écart type

1. Calculer la moyenne de l`échantillon. Pour déterminer l`erreur type, vous devez d`abord calculer l`écart type (car l`écart type, s, fait partie de la formule de l`erreur type). Commencez par calculer la moyenne des valeurs de l`échantillon. La moyenne de l`échantillon est exprimée comme la moyenne arithmétique des mesures x1, x2, . . . xn. Ceci est calculé avec la formule ci-dessus.
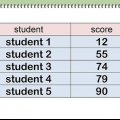
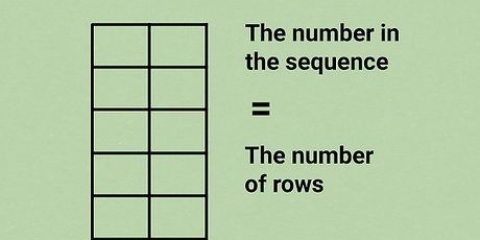
- Par exemple, supposons que vous deviez calculer l`erreur standard d`une moyenne d`échantillon pour les mesures du poids de cinq pièces, comme indiqué dans le tableau ci-dessous :
Vous calculeriez ensuite la moyenne de l`échantillon en entrant les valeurs de poids dans la formule, comme ceci :

2. Soustraire la moyenne de l`échantillon de chaque mesure et mettre cette valeur au carré. Une fois que vous avez la moyenne de l`échantillon, vous pouvez développer le tableau en le soustrayant de chaque mesure individuelle, puis en mettant le résultat au carré.

3. Déterminez l`écart total de vos lectures par rapport à la moyenne de l`échantillon. L`écart total est la moyenne de la différence au carré par rapport à la moyenne de l`échantillon. Additionnez toutes les valeurs ensemble pour déterminer cela.
Cette équation vous donne l`écart total au carré des lectures par rapport à la moyenne de l`échantillon. Notez que le signe de la différence n`a pas d`importance.

4. Calculer l`écart quadratique moyen des mesures par rapport à la moyenne de l`échantillon. Une fois que vous connaissez l`écart total, vous pouvez trouver l`écart moyen en utilisant n -1. Notez que n est égal au nombre de mesures.

5. Déterminer l`écart type. Vous avez maintenant toutes les valeurs nécessaires pour utiliser la formule d`écart(s) type.
L`écart type est donc de 0,0071624.
Partie 3 sur 3 : Détermination de l`erreur standard

1. Utilisez l`écart type pour calculer l`erreur standard avec la formule standard.
- Dans l`exemple ci-dessus, vous calculez l`erreur standard comme suit :
L`erreur type (l`écart type de la moyenne de l`échantillon) est donc de 0,0032031 grammes.
Des astuces
- L`erreur type et l`écart type sont souvent confondus. Notez que l`erreur standard est une description de l`écart type de la distribution d`échantillonnage d`une valeur statistique, et non la distribution des valeurs individuelles.
- Dans les revues scientifiques, l`erreur-type et l`écart-type sont parfois utilisés de manière interchangeable. Un signe ± est utilisé pour joindre les deux lectures.
Articles sur le sujet "Calcul de l'erreur standard"
Оцените, пожалуйста статью
Populaire