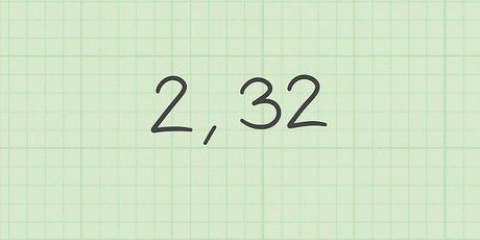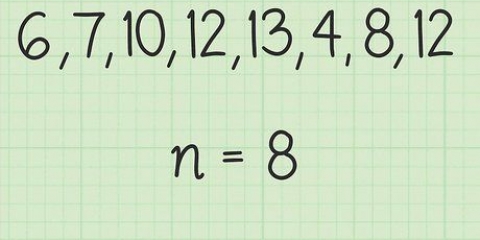Calcul de la séquence de Fibonacci (avec des images)

Teneur

Pas
- Méthode 1 sur 2: Utiliser un tableau
- Méthode 2 sur 2: Utilisation de la formule de Binet et du nombre d`or

La suite de Fibonacci est une suite de nombres générés en additionnant les deux nombres précédents de la suite. Les nombres de la série sont fréquemment vus dans la nature et dans l`art, tels que les spirales et le nombre d`or. La façon la plus simple de calculer la série est de préparer un tableau ; cependant, ce n`est pas pratique si vous recherchez le 100e terme de la séquence, par exemple, auquel cas vous utiliserez la formule de Binet.

Pas

Méthode 1 sur 2: Utiliser un tableau

Image intitulée Calculer la séquence de Fibonacci Étape 1

1. Créer un tableau avec deux colonnes. Le nombre de lignes dépend du nombre de nombres dans la séquence de Fibonacci que vous souhaitez calculer.

Par exemple, si vous voulez trouver le cinquième nombre de la séquence, votre tableau aura cinq lignes.
Avec cette méthode de table, il n`est pas possible de trouver un nombre plus bas dans la séquence sans d`abord calculer tous les nombres qui le précèdent. Par exemple, si vous voulez trouver le 100e nombre dans la séquence, vous devrez d`abord trouver les 99 premiers nombres. Par conséquent, la méthode du tableau ne fonctionne que pour les nombres au début de la séquence.

Image intitulée Calculer la séquence de Fibonacci Étape 2

2. Entrez la séquence de nombres dans la colonne de gauche. Cela signifie remplir une séquence de nombres ordinaux consécutifs, en commençant par "1er."

Le terme fait référence à la position du nombre dans la séquence de Fibonacci.

Par exemple, si vous voulez calculer le cinquième nombre de la séquence, vous écririez 1er, 2e, 3e, 4e, 5e dans la colonne de gauche. Cela vous aidera à identifier les cinq premiers termes de la séquence.

Image intitulée Calculer la séquence de Fibonacci Étape 3

3. Mettez 1 dans la première ligne de la colonne de droite. C`est le point de départ de la suite de Fibonacci. En d`autres termes, le premier terme de la suite est 1.

La séquence de Fibonacci correcte commence toujours par 1. Si vous voulez commencer avec un nombre différent, vous ne trouverez pas le bon motif de la séquence de Fibonacci.

Image intitulée Calculer la séquence de Fibonacci Étape 4

4. Compter le premier terme (1) et 0. ensemble sur. Cela vous donnera le deuxième numéro de la séquence.

Rappelons que pour trouver un nombre donné de la suite de Fibonacci, il suffit d`additionner les deux nombres précédents ensemble.

Pour créer la séquence, 0 vient avant 1 (le premier terme), donc : 1 + 0 = 1.

Image intitulée Calculer la séquence de Fibonacci Étape 5

5. Additionner le premier terme (1) et le deuxième terme (1) ensemble. Cela vous donnera le troisième numéro de la séquence.

1 + 1 = 2. Le troisième terme est 2.

Image intitulée Calculer la séquence de Fibonacci Étape 6

6. Additionnez le deuxième terme (1) et le troisième terme (2) pour obtenir le quatrième nombre de la séquence.

1 + 2 = 3. Le quatrième terme est 3.

Image intitulée Calculer la séquence de Fibonacci Étape 7

sept. Additionner le troisième terme (2) et le quatrième terme (3) ensemble. Vous connaissez maintenant le cinquième nombre de la séquence.

2 + 3 = 5. Le cinquième terme est 5.

Image intitulée Calculer la séquence de Fibonacci Étape 8

8. Additionnez les deux nombres précédents pour trouver un nombre donné dans la séquence de Fibonacci. Si vous utilisez cette méthode, vous utilisez la formule

F m = F_{m - 1} + F_{m - 2}

$F_{{n}}=F_{{n-1}}+F_{{n-2}}$ . Parce qu`il ne s`agit pas d`une formule fermée, vous ne pouvez pas l`utiliser pour calculer chaque terme de la série sans d`abord calculer tous les nombres précédents.

Méthode 2 sur 2: Utilisation de la formule de Binet et du nombre d`or

Image intitulée Calculer la séquence de Fibonacci Étape 9

1. Écrivez la formule :

X m

$x_{{n}}$ =

?? m - (1 - ??)^{m} \sqrt{5}

${frac{phi ^{{n}}-(1-phi )^{{n}}}{{sqrt{5}}}}$ . Dans la formule,

X m

$x_{{n}}$ = le terme dans la séquence que vous essayez de trouver,

m

$m$ = le numéro de position du terme dans la série, et

??

$phi$ = le nombre d`or.

Il s`agit d`une formule fermée, vous pouvez donc calculer un terme spécifique de la série sans avoir à calculer tous les précédents.
Cette formule est une formule simplifiée dérivée de la formule de Fibonacci de Binet.
La formule applique le nombre d`or ( $??$ $phi$ ), car le rapport de deux nombres consécutifs dans la suite de Fibonacci est très similaire au nombre d`or.

Image intitulée Calculer la séquence de Fibonacci Étape 10

2. Ajustez le nombre pour m{style d`affichage n} $m$ appliquer à la formule. le

m

$m$ représente le terme que vous recherchez dans la séquence.

Par exemple, si vous recherchez le cinquième nombre de la séquence, saisissez 5. Votre formule devrait maintenant ressembler à ceci :

X 5

$x_{{5}}$ =

?? 5 - (1 - ??)^{5} \sqrt{5}

${frac{phi ^{{5}}-(1-phi )^{{5}}}{{sqrt{5}}}}$ .

Image intitulée Calculer la séquence de Fibonacci Étape 11

3. Remplacer le nombre d`or dans la formule. Utilisez 1,618034 comme approximation du nombre d`or.

Par exemple, si vous recherchez le cinquième nombre dans la séquence, la formule que vous avez saisie ressemblera à ceci :

X 5

$x_{{5}}$ =

(1, 618034) 5 - (1 - 1, 618034)^{5} \sqrt{5}

${frac{(1.618034)^{{5}}-(1-1,618034)^{{5}}}{{sqrt{5}}}}$ .

Image intitulée Calculer la séquence de Fibonacci Étape 12

4. Complétez les calculs entre parenthèses. Considérez l`ordre des opérations arithmétiques en calculant d`abord la partie entre parenthèses :

1 - 1, 618034 = - 0, 618034

$1-1.618034=-0.618034$ .

Dans l`exemple, l`équation devient

X 5

$x_{{5}}$ =

(1, 618034) 5 - (- 0, 618034)^{5} \sqrt{5}

${frac{(1.618034)^{{5}}-(-0.618034)^{{5}}}{{sqrt{5}}}}$ .

Image intitulée Calculer la séquence de Fibonacci Étape 13

5. Calculer les exposants. Multiplier les deux nombres entre parenthèses dans le numérateur par l`exposant approprié.

Dans l`exemple,

1, 618034 5 = 11, 090170

$1.618034^{{5}}=11.090170$ ;

- 0, 618034 5 = - 0, 090169

$-0.618034^{{5}}=-0.090169$ . L`équation devient donc

X 5 = 11, 090170 - (- 0, 090169) \sqrt{5}

$x_{{5}}={frac{11,090170-(-0,090169)}{{sqrt{5}}}}$ .

Image intitulée Calculer la séquence de Fibonacci Étape 14

6. Compléter le calcul. Avant de continuer à diviser, vous devez d`abord soustraire les deux nombres au numérateur.

Dans l`exemple,

11, 090170 - (- 0, 090169) = 11, 180339

$11.090170-(-0.090169)=11.180339$ , donc l`équation devient

X 5

$x_{{5}}$ =

11, 180339 \sqrt{5}

${frac{11,180339}{{sqrt{5}}}}$ .

Image intitulée Calculer la séquence de Fibonacci Étape 15

sept. Diviser par la racine carrée de cinq. La racine carrée de cinq est arrondie à 2.236067.

Dans l`exemple d`affectation,

11, 180339 2, 236067 = 5, 000002

${frac{11,180339}{2,236067}}=5,000002$ .

Image intitulée Calculer la séquence de Fibonacci Étape 16

8. Arrondir au nombre entier le plus proche. Votre réponse est un nombre décimal, mais est très proche d`un entier. Cet entier représente le nombre dans la séquence de Fibonacci.

Si vous avez utilisé le nombre d`or complet et n`avez rien arrondi, vous obtiendrez un nombre entier. Cependant, il est plus pratique d`arrondir, ce qui se traduira par un nombre décimal.

Dans l`exemple, votre réponse, calculée avec une calculatrice, sera d`environ 5 000002. Arrondi au nombre entier le plus proche, votre réponse sera cinq, qui sera également le cinquième nombre de la séquence de Fibonacci.