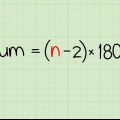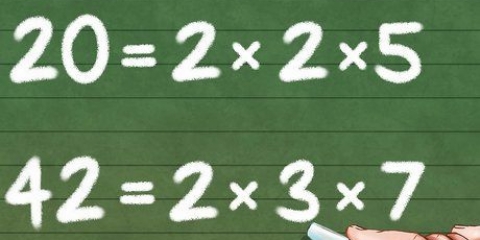Par exemple, si vous voulez calculer la somme des séries 10, 15, 20, 25, 30, alors  , car il y a cinq nombres dans la séquence.
, car il y a cinq nombres dans la séquence. 
Par exemple, dans la séquence 10, 15, 20, 25, 30  , et
, et  .
. 

Par exemple, s`il y a cinq nombres dans votre séquence, où 10 est le premier nombre et 30 est le dernier nombre, votre formule ressemblera à ceci :  .
. 
Par exemple:



Par exemple:


Donc la somme des séries (10, 15, 20, 25, 30) est égale à 100. 

Déterminer le nombre de nombres ( ) dans la serie. Puisque vous commencez par trois, terminez par 24 et ajoutez sept à chaque fois, la séquence de nombres est 3, 10, 17, 24. (Le facteur de différence est la différence entre chaque nombre de la série.) Cela signifie que
) dans la serie. Puisque vous commencez par trois, terminez par 24 et ajoutez sept à chaque fois, la séquence de nombres est 3, 10, 17, 24. (Le facteur de différence est la différence entre chaque nombre de la série.) Cela signifie que 
Déterminez le premier ( ) enfin (
) enfin ( ) numéro dans la séquence. Puisque la séquence va de 3 à 24,
) numéro dans la séquence. Puisque la séquence va de 3 à 24,  et
et  .
. Trouver la moyenne de  et
et  :
:  .
. Multipliez la moyenne par  :
:  .
. 
Déterminer le nombre de termes ( ) dans la serie. Parce que Mara économise pendant 52 semaines, (1 an),
) dans la serie. Parce que Mara économise pendant 52 semaines, (1 an),  .
. Déterminez le premier ( ) enfin (
) enfin ( ) numéro dans la séquence. Le premier montant qu`elle économise est de cinq euros, alors
) numéro dans la séquence. Le premier montant qu`elle économise est de cinq euros, alors  . Pour calculer le montant total épargné au cours de la dernière semaine de l`année, nous calculons
. Pour calculer le montant total épargné au cours de la dernière semaine de l`année, nous calculons  . alors
. alors  .
. Détermine la moyenne de  et
et  :
:  .
. Multipliez la moyenne par  :
:  . Elle a donc économisé 6 890 € en fin d`année.
. Elle a donc économisé 6 890 € en fin d`année.
Trouver la somme d'une suite arithmétique
Teneur
Une suite arithmétique est une suite de nombres où chaque nombre augmente d`une valeur constante. Pour la somme d`une suite arithmétique, vous pouvez additionner tous les nombres ensemble. Cependant, ce n`est pas vraiment pratique lorsque la séquence contient un grand nombre de termes. Au lieu de cela, vous pouvez rapidement trouver la somme de chaque séquence arithmétique en multipliant la moyenne du premier et du dernier nombre par le nombre de termes de la séquence.
Pas
Partie 1 sur 3: Analyser votre séquence

1. Assurez-vous d`avoir une suite arithmétique. Une séquence arithmétique est une liste ordonnée de nombres, où le changement des nombres est constant. Cette méthode ne fonctionne que si votre ensemble de nombres est une séquence arithmétique.
- Pour déterminer si vous avez affaire à une suite arithmétique, trouvez la différence entre la première ou la dernière paire de nombres. Assurez-vous que la différence est toujours la même.
- Par exemple, la suite des nombres 10, 15, 20, 25, 30 est une suite arithmétique, car la différence entre chaque nombre est constamment de cinq.

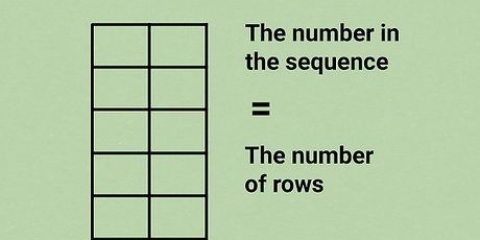
2. Déterminez le nombre de termes de votre séquence. Chaque nombre est un terme. Si un seul chiffre est mentionné, vous pouvez les compter. Si vous connaissez le premier nombre, le dernier nombre et le facteur de différence (la différence entre chaque nombre), vous pouvez utiliser une formule pour déterminer le nombre de nombres. Ce nombre est présenté par la variable  .
.
 .
. , car il y a cinq nombres dans la séquence.
, car il y a cinq nombres dans la séquence.
3. Trouver le premier et le dernier nombre de la séquence. Vous devez connaître les deux nombres pour calculer la somme de la suite arithmétique. Souvent, le premier nombre sera un, mais pas toujours. Définir la variable  égal au premier nombre de la séquence, et
égal au premier nombre de la séquence, et  égal au dernier nombre de la séquence.
égal au dernier nombre de la séquence.
 égal au premier nombre de la séquence, et
égal au premier nombre de la séquence, et  égal au dernier nombre de la séquence.
égal au dernier nombre de la séquence. , et
, et  .
.Partie 2 sur 3: Calculer la somme

1. Écrire la formule pour trouver la somme d`une suite arithmétique. La formule est  , par lequel
, par lequel  est égal à la somme de la série.
est égal à la somme de la série.
 , par lequel
, par lequel  est égal à la somme de la série.
est égal à la somme de la série. - Notez que cette formule indique que la somme de la séquence arithmétique est égale à la moyenne du premier et du dernier nombre multipliée par le nombre de nombres.

2. Entrez les valeurs m  ,
, une 1  et
et une m  dans la formule de. Assurez-vous de remplacer correctement.
dans la formule de. Assurez-vous de remplacer correctement.
 ,
,  et
et  dans la formule de. Assurez-vous de remplacer correctement.
dans la formule de. Assurez-vous de remplacer correctement. .
.
3. Calculer la moyenne du premier et du deuxième nombre. Vous faites cela en additionnant les deux nombres et en divisant par deux.



4. Multiplier la moyenne par le nombre de nombres de la série. Cela vous donne la somme de la suite arithmétique.


Donc la somme des séries (10, 15, 20, 25, 30) est égale à 100.
Partie 3 sur 3 : Résoudre les exemples de problèmes

1. Trouver la somme des nombres de 1 à 500. Inclure tous les entiers consécutifs dans le calcul.
- Déterminer le nombre de termes (
) dans la serie. Puisque vous comptez tous les entiers consécutifs jusqu`à et y compris 500,
.
- Déterminez le premier (
) enfin (
) numéro dans la séquence. Étant donné que nous supposons les séries 1 à 500, il retient que
et
.
- Trouver la moyenne de
et
:
.
- Multipliez la moyenne par
:
.

2. Trouver la somme de la suite arithmétique indiquée. Le premier nombre de la séquence est trois. Le dernier chiffre de la séquence est 24. Le facteur de différence est de sept.
 ) dans la serie. Puisque vous commencez par trois, terminez par 24 et ajoutez sept à chaque fois, la séquence de nombres est 3, 10, 17, 24. (Le facteur de différence est la différence entre chaque nombre de la série.) Cela signifie que
) dans la serie. Puisque vous commencez par trois, terminez par 24 et ajoutez sept à chaque fois, la séquence de nombres est 3, 10, 17, 24. (Le facteur de différence est la différence entre chaque nombre de la série.) Cela signifie que 
 ) enfin (
) enfin ( ) numéro dans la séquence. Puisque la séquence va de 3 à 24,
) numéro dans la séquence. Puisque la séquence va de 3 à 24,  et
et  .
. et
et  :
:  .
. :
:  .
.
3. Résoudre le problème suivant. Mara économise 5 euros la première semaine de l`année. Le reste de l`année, elle augmente son épargne de 5 euros chaque semaine. Combien d`argent Mara a-t-elle économisé à la fin de l`année?
 ) dans la serie. Parce que Mara économise pendant 52 semaines, (1 an),
) dans la serie. Parce que Mara économise pendant 52 semaines, (1 an),  .
. ) enfin (
) enfin ( ) numéro dans la séquence. Le premier montant qu`elle économise est de cinq euros, alors
) numéro dans la séquence. Le premier montant qu`elle économise est de cinq euros, alors  . Pour calculer le montant total épargné au cours de la dernière semaine de l`année, nous calculons
. Pour calculer le montant total épargné au cours de la dernière semaine de l`année, nous calculons  . alors
. alors  .
. et
et  :
:  .
. :
:  . Elle a donc économisé 6 890 € en fin d`année.
. Elle a donc économisé 6 890 € en fin d`année.Articles sur le sujet "Trouver la somme d'une suite arithmétique"
Оцените, пожалуйста статью
Similaire
Populaire