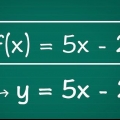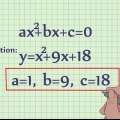Prenons l`exemple de comparaison  , où les termes y peuvent être déplacés vers la gauche en soustrayant un y des deux côtés. Les autres termes peuvent être déplacés vers la droite en ajoutant 6 des deux côtés et
, où les termes y peuvent être déplacés vers la gauche en soustrayant un y des deux côtés. Les autres termes peuvent être déplacés vers la droite en ajoutant 6 des deux côtés et  tirer des deux côtés. L`équation résultante est
tirer des deux côtés. L`équation résultante est  .
. 
Voir l`exemple de comparaison  . Il n`y a pas de limitation sur les valeurs autorisées de x pour cette équation. Cependant, vous devez comprendre qu`il s`agit de l`équation d`une parabole, avec x=0 comme centre, et qu`une parabole n`est pas une fonction car ce n`est pas une comparaison un à un des valeurs x et y. Pour limiter cette équation et en faire une fonction, pour laquelle nous pouvons trouver un inverse, nous devons définir le domaine comme x≥0.
. Il n`y a pas de limitation sur les valeurs autorisées de x pour cette équation. Cependant, vous devez comprendre qu`il s`agit de l`équation d`une parabole, avec x=0 comme centre, et qu`une parabole n`est pas une fonction car ce n`est pas une comparaison un à un des valeurs x et y. Pour limiter cette équation et en faire une fonction, pour laquelle nous pouvons trouver un inverse, nous devons définir le domaine comme x≥0. La gamme est limitée de la même manière. A noter que le premier terme,  , sera toujours positif ou 0, pour toute valeur de x. Ensuite, si l`équation ajoute +2, la plage sera n`importe quelle valeur y≥2.
, sera toujours positif ou 0, pour toute valeur de x. Ensuite, si l`équation ajoute +2, la plage sera n`importe quelle valeur y≥2. Il est nécessaire de définir le domaine et la portée à ce stade précoce. Vous utiliserez ces définitions plus tard lors de la définition du domaine et de la portée de la fonction inverse. En fait, le domaine de la fonction d`origine devient le domaine de la fonction inverse, et le domaine de la fonction d`origine devient le domaine de l`inverse. 
Travailler avec l`exemple de comparaison  , cette étape d`inversion aboutira à la nouvelle équation de
, cette étape d`inversion aboutira à la nouvelle équation de  .
. Un autre format consiste à remplacer les termes y par x, mais remplacer les termes x par soit  ou
ou  pour indiquer la fonction inverse.
pour indiquer la fonction inverse. 
 (prémisse d`origine)
(prémisse d`origine) (soustrayez 2 des deux côtés)
(soustrayez 2 des deux côtés) (diviser les deux côtés par 2)
(diviser les deux côtés par 2)± (racine carrée des deux côtés ; rappelez-vous que la racine carrée donne des réponses possibles positives et négatives)
(racine carrée des deux côtés ; rappelez-vous que la racine carrée donne des réponses possibles positives et négatives) 
Voir la solution de l`exemple d`équation ± . Comme la fonction racine carrée n`est pas définie pour les valeurs négatives, le terme . doit être
. Comme la fonction racine carrée n`est pas définie pour les valeurs négatives, le terme . doit être  toujours être positif. Par conséquent, les valeurs autorisées de x (le domaine) doivent être x≥2. Avec cela comme domaine, les valeurs résultantes de y (la plage) sont soit toutes les valeurs y≥0, si vous prenez la solution positive de la racine carrée, soit y≤0, si vous prenez la solution négative de la racine carrée. Notez que pour trouver la fonction inverse, vous avez initialement défini le domaine comme x≥0. Par conséquent, la solution correcte pour la fonction inverse est l`option positive.
toujours être positif. Par conséquent, les valeurs autorisées de x (le domaine) doivent être x≥2. Avec cela comme domaine, les valeurs résultantes de y (la plage) sont soit toutes les valeurs y≥0, si vous prenez la solution positive de la racine carrée, soit y≤0, si vous prenez la solution négative de la racine carrée. Notez que pour trouver la fonction inverse, vous avez initialement défini le domaine comme x≥0. Par conséquent, la solution correcte pour la fonction inverse est l`option positive. Comparez le domaine et la plage de l`inverse avec le domaine et la plage de l`original. Rappelez-vous que pour la fonction d`origine,  , le domaine a été défini comme toutes les valeurs de x≥0, et la plage a été définie comme toutes les valeurs de y≥2. Pour la fonction inverse, maintenant ces valeurs s`échangent, et le domaine est toutes les valeurs de x≥2, et la plage est toutes les valeurs de y≥0.
, le domaine a été défini comme toutes les valeurs de x≥0, et la plage a été définie comme toutes les valeurs de y≥2. Pour la fonction inverse, maintenant ces valeurs s`échangent, et le domaine est toutes les valeurs de x≥2, et la plage est toutes les valeurs de y≥0. 
A titre d`exemple, choisissez la valeur x=1 pour l`équation d`origine  . Cela donne le résultat y=4.
. Cela donne le résultat y=4. Ensuite tu mets la valeur 4 dans la fonction inverse  . Cela donne en effet le résultat y=1. Vous pouvez conclure que votre fonction inverse est correcte.
. Cela donne en effet le résultat y=1. Vous pouvez conclure que votre fonction inverse est correcte. 

Notez que cette forme standard consiste en un terme quadratique parfait,  , qui est ensuite modifié par les deux autres éléments a et k. Pour arriver à cette forme quadratique parfaite, vous devrez créer certaines conditions dans votre équation quadratique.
, qui est ensuite modifié par les deux autres éléments a et k. Pour arriver à cette forme quadratique parfaite, vous devrez créer certaines conditions dans votre équation quadratique. 
Pour compléter le carré, tricoter en sens inverse. Tu commences par  et un deuxième terme x. A partir du coefficient de ce terme, que vous pouvez définir comme « 2b », vous devez obtenir
et un deuxième terme x. A partir du coefficient de ce terme, que vous pouvez définir comme « 2b », vous devez obtenir  voir pour trouver. Cela nécessite une combinaison de division par deux puis de quadrature de ce résultat.
voir pour trouver. Cela nécessite une combinaison de division par deux puis de quadrature de ce résultat. 
Prenons, par exemple, la fonction quadratique  . Vous pouvez simplifier cela en divisant tous les termes par 2 pour obtenir la fonction résultante
. Vous pouvez simplifier cela en divisant tous les termes par 2 pour obtenir la fonction résultante  pour obtenir. Le coefficient 2 reste en dehors des parenthèses et fera partie de votre solution finale.
pour obtenir. Le coefficient 2 reste en dehors des parenthèses et fera partie de votre solution finale. Si tous les termes ne sont pas des multiples de a, vous obtenez des coefficients fractionnaires. Par exemple : la fonction  sera simplifié pour
sera simplifié pour  . Travaillez soigneusement les fractions.
. Travaillez soigneusement les fractions. 
Par exemple, si les deux premiers termes de votre fonction quadratique  vous trouvez le troisième terme nécessaire en divisant 3 par 2 (ou 3/2), puis en le carré, pour obtenir 9/4. Le quadratique
vous trouvez le troisième terme nécessaire en divisant 3 par 2 (ou 3/2), puis en le carré, pour obtenir 9/4. Le quadratique  est un carré parfait.
est un carré parfait. Autre exemple : supposons que les deux premiers termes  sont. La moitié du moyen terme est -2, puis vous le carré pour obtenir 4. Le carré parfait résultant est
sont. La moitié du moyen terme est -2, puis vous le carré pour obtenir 4. Le carré parfait résultant est  .
. 
Supposons que vous ayez la fonction  . Comme mentionné ci-dessus, vous utilisez les deux premiers termes pour compléter le carré. En utilisant le terme moyen de -4x, vous générez un troisième terme +4. Ajouter 4 et soustraire 4 de l`équation, sous la forme
. Comme mentionné ci-dessus, vous utilisez les deux premiers termes pour compléter le carré. En utilisant le terme moyen de -4x, vous générez un troisième terme +4. Ajouter 4 et soustraire 4 de l`équation, sous la forme  . Les parenthèses ne sont placées que pour définir l`équation quadratique que vous faites. Notez le +4 à l`intérieur des crochets et le -4 à l`extérieur. Simplifier les nombres au résultat
. Les parenthèses ne sont placées que pour définir l`équation quadratique que vous faites. Notez le +4 à l`intérieur des crochets et le -4 à l`extérieur. Simplifier les nombres au résultat  .
. 
A noter que pour cette fonction a=1, h=2 et k=5. La valeur d`écrire l`équation sous cette forme est que a, parce qu`elle est positive, elle vous indique que la parabole pointe vers le haut. Les valeurs (h, k) indiquent le sommet au bas de la parabole, si vous vouliez le représenter graphiquement. 
Continuer à travailler avec la fonction de prévisualisation  . Comme il s`agit d`un format standard, vous pouvez déterminer le sommet sous la forme x=2, y=5. Donc, pour éviter la symétrie, vous ne travaillez qu`avec le côté droit du graphique et définissez le domaine si toutes les valeurs x≥2. L`insertion de la valeur x=2 dans la fonction renvoie y=5. Vous pouvez voir que les valeurs de y augmenteront à mesure que x augmente. Par conséquent, l`étendue de cette équation est y≥5.
. Comme il s`agit d`un format standard, vous pouvez déterminer le sommet sous la forme x=2, y=5. Donc, pour éviter la symétrie, vous ne travaillez qu`avec le côté droit du graphique et définissez le domaine si toutes les valeurs x≥2. L`insertion de la valeur x=2 dans la fonction renvoie y=5. Vous pouvez voir que les valeurs de y augmenteront à mesure que x augmente. Par conséquent, l`étendue de cette équation est y≥5. 
Continuer à travailler avec la fonction  . Insérez x à la place de f(x) et insérez y (ou f(x), si vous préférez) à la place de x. Cela donne comme nouvelle fonction
. Insérez x à la place de f(x) et insérez y (ou f(x), si vous préférez) à la place de x. Cela donne comme nouvelle fonction  .
. 
 (point de départ initial)
(point de départ initial) (soustrayez 5 des deux côtés)
(soustrayez 5 des deux côtés)± (racine carrée des deux côtés ; rappelez-vous que la racine carrée donne des réponses possibles positives et négatives)
(racine carrée des deux côtés ; rappelez-vous que la racine carrée donne des réponses possibles positives et négatives) ± (ajouter 2 des deux côtés)
(ajouter 2 des deux côtés) 
Voir la solution de l`exemple d`équation ± . Comme la fonction racine carrée n`est pas définie pour les valeurs négatives, le terme . doit être
. Comme la fonction racine carrée n`est pas définie pour les valeurs négatives, le terme . doit être  toujours être positif. Par conséquent, les valeurs autorisées de x (le domaine) doivent être x≥5. Avec cela comme domaine, les valeurs résultantes de y (la plage) sont soit toutes les valeurs y≥2 (si vous prenez la solution positive de la racine carrée), soit y≤2 (si vous choisissez la solution négative de la racine carrée). Rappelez-vous que vous avez initialement défini le domaine comme x≥2, afin de trouver la fonction inverse. Par conséquent, la solution correcte pour la fonction inverse est l`option positive.
toujours être positif. Par conséquent, les valeurs autorisées de x (le domaine) doivent être x≥5. Avec cela comme domaine, les valeurs résultantes de y (la plage) sont soit toutes les valeurs y≥2 (si vous prenez la solution positive de la racine carrée), soit y≤2 (si vous choisissez la solution négative de la racine carrée). Rappelez-vous que vous avez initialement défini le domaine comme x≥2, afin de trouver la fonction inverse. Par conséquent, la solution correcte pour la fonction inverse est l`option positive. Comparez le domaine et la plage de l`inverse avec le domaine et la plage de l`original. Rappelons que pour la fonction d`origine, le domaine a été défini comme toutes les valeurs de x≥2, et la plage a été définie comme toutes les valeurs de y≥5. Pour cette fonction inverse, ces valeurs s`échangent, et le domaine est maintenant toutes les valeurs de x≥5, et la plage est toutes les valeurs de y≥2. 
A titre d`exemple, choisissez la valeur x=3 à inclure dans l`équation d`origine  procéder. Cela donne le résultat y=6.
procéder. Cela donne le résultat y=6. Ensuite, vous traitez y=6 dans la fonction inverse  . Cela renvoie y=3, qui est le nombre avec lequel vous avez commencé. Vous pouvez conclure que votre fonction inverse est correcte.
. Cela renvoie y=3, qui est le nombre avec lequel vous avez commencé. Vous pouvez conclure que votre fonction inverse est correcte. 

Pour cette section de cet article, vous utiliserez l`exemple d`équation  .
. 

Basé sur l`équation du travail  , est-ce que cela donne le résultat
, est-ce que cela donne le résultat  .
. 
Pour l`exemple d`équation, pour obtenir le côté gauche égal à zéro, vous devez soustraire x des deux côtés de l`équation. Cela donne le résultat  .
. 
Laisser  . Donc, x=1
. Donc, x=1 Laisser  . Donc, b=2
. Donc, b=2 Laisser  . Donc, c=(-3-x)
. Donc, c=(-3-x) 
x=[-b±√(b^2-4ac)]/2a x=(-2)±√((-2)^2-4(1)(-3-x)) / 2(1) x=((-2)±√(4+12+4x)))/2 x=(-2±√(16+4x))/2 x=(-2±√(4)(4+x)))/2 x=-2±2√(4+x))/2 x=-1±√(4+x) f-inverse = -1±√(4+x)(Cette dernière étape est possible car vous avez échangé f(x) pour la variable x à un stade antérieur). 




Assumer la fonction d`origine  , choisissez votre x=-2. Cela renvoie y=-3. Remplacez maintenant la valeur de x=-3 dans la fonction inverse,
, choisissez votre x=-2. Cela renvoie y=-3. Remplacez maintenant la valeur de x=-3 dans la fonction inverse,  . Cela renvoie -2, qui est bien la valeur avec laquelle vous avez commencé. Donc ta définition de la fonction inverse est correcte.
. Cela renvoie -2, qui est bien la valeur avec laquelle vous avez commencé. Donc ta définition de la fonction inverse est correcte.
Trouver l'inverse d'une équation quadratique
Teneur
Les fonctions inverses peuvent être très utiles pour résoudre de nombreux problèmes mathématiques. Être capable de prendre une fonction et de trouver sa fonction inverse est un outil puissant. Cependant, avec les équations quadratiques, cela peut être un processus assez compliqué. Vous devez d`abord définir soigneusement l`équation, en déterminant un domaine et une plage appropriés. Vous avez alors le choix entre trois méthodes pour calculer la fonction inverse. Le choix de la méthode est principalement une question de préférence personnelle.
Pas
Méthode 1 sur 3: Trouver l`inverse d`une fonction simple

1. Trouver une fonction sous la forme de oui = une X 2 + c  . Si vous avez le "bon" type de fonction pour commencer, vous pouvez trouver l`inverse avec une simple algèbre. Cette forme est une sorte de variation sur
. Si vous avez le "bon" type de fonction pour commencer, vous pouvez trouver l`inverse avec une simple algèbre. Cette forme est une sorte de variation sur  . Si vous comparez cela avec une fonction quadratique standard,
. Si vous comparez cela avec une fonction quadratique standard,  , voir que le moyen terme
, voir que le moyen terme  est manquant. Une autre façon de dire cela est que la valeur de b est zéro. Si votre fonction a cette forme, trouver l`inverse est assez facile.
est manquant. Une autre façon de dire cela est que la valeur de b est zéro. Si votre fonction a cette forme, trouver l`inverse est assez facile.
 . Si vous avez le "bon" type de fonction pour commencer, vous pouvez trouver l`inverse avec une simple algèbre. Cette forme est une sorte de variation sur
. Si vous avez le "bon" type de fonction pour commencer, vous pouvez trouver l`inverse avec une simple algèbre. Cette forme est une sorte de variation sur  . Si vous comparez cela avec une fonction quadratique standard,
. Si vous comparez cela avec une fonction quadratique standard,  , voir que le moyen terme
, voir que le moyen terme  est manquant. Une autre façon de dire cela est que la valeur de b est zéro. Si votre fonction a cette forme, trouver l`inverse est assez facile.
est manquant. Une autre façon de dire cela est que la valeur de b est zéro. Si votre fonction a cette forme, trouver l`inverse est assez facile. - Votre fonction de départ ne doit pas nécessairement ressembler exactement à
. Tant que vous pouvez le regarder et voir que la fonction se compose uniquement de
termes et nombres constants, vous pourrez utiliser cette méthode.
- Supposons que vous commenciez par l`équation
. Un examen rapide de cette équation révèle qu`il n`y a pas de termes de
être à la première puissance. Cette équation est un candidat pour cette méthode pour trouver une fonction inverse.

2. Simplifier en combinant des termes similaires. L`équation initiale peut avoir plusieurs termes dans une combinaison d`addition et de soustraction. Votre première étape consiste à combiner des termes similaires pour simplifier l`équation et la réécrire dans le format standard  .
.
 .
. , où les termes y peuvent être déplacés vers la gauche en soustrayant un y des deux côtés. Les autres termes peuvent être déplacés vers la droite en ajoutant 6 des deux côtés et
, où les termes y peuvent être déplacés vers la gauche en soustrayant un y des deux côtés. Les autres termes peuvent être déplacés vers la droite en ajoutant 6 des deux côtés et  tirer des deux côtés. L`équation résultante est
tirer des deux côtés. L`équation résultante est  .
.
3. Déterminer le domaine et l`étendue de la fonction simplifiée. Rappelons que le domaine d`une fonction est constitué des valeurs possibles de x qui peuvent être appliquées pour donner une solution réelle. La plage d`une fonction se compose des valeurs de y qui retourneront. Pour déterminer le domaine de la fonction, recherchez des valeurs qui produisent un résultat mathématiquement impossible. Vous indiquez ensuite le domaine si toutes les autres valeurs de x. Pour trouver la plage, considérez les valeurs de y à des points limites arbitraires et examinez le comportement de la fonction.
 . Il n`y a pas de limitation sur les valeurs autorisées de x pour cette équation. Cependant, vous devez comprendre qu`il s`agit de l`équation d`une parabole, avec x=0 comme centre, et qu`une parabole n`est pas une fonction car ce n`est pas une comparaison un à un des valeurs x et y. Pour limiter cette équation et en faire une fonction, pour laquelle nous pouvons trouver un inverse, nous devons définir le domaine comme x≥0.
. Il n`y a pas de limitation sur les valeurs autorisées de x pour cette équation. Cependant, vous devez comprendre qu`il s`agit de l`équation d`une parabole, avec x=0 comme centre, et qu`une parabole n`est pas une fonction car ce n`est pas une comparaison un à un des valeurs x et y. Pour limiter cette équation et en faire une fonction, pour laquelle nous pouvons trouver un inverse, nous devons définir le domaine comme x≥0. , sera toujours positif ou 0, pour toute valeur de x. Ensuite, si l`équation ajoute +2, la plage sera n`importe quelle valeur y≥2.
, sera toujours positif ou 0, pour toute valeur de x. Ensuite, si l`équation ajoute +2, la plage sera n`importe quelle valeur y≥2.
4. Échanger les rôles des termes x et y. Sans changer l`équation d`aucune autre manière, vous devez remplacer toutes les formes de y par x et toutes les formes de x par y. C`est l`étape qui "inverse" réellement l`équation.
 , cette étape d`inversion aboutira à la nouvelle équation de
, cette étape d`inversion aboutira à la nouvelle équation de  .
. ou
ou  pour indiquer la fonction inverse.
pour indiquer la fonction inverse.
5. Réécrire l`équation inverse en fonction de y. En utilisant une combinaison d`étapes algébriques et en vous assurant que la même opération est effectuée des deux côtés de l`équation, vous devrez isoler la variable y. Pour la comparaison  , cette révision ressemble à ceci :
, cette révision ressemble à ceci :
 , cette révision ressemble à ceci :
, cette révision ressemble à ceci : (prémisse d`origine)
(prémisse d`origine) (soustrayez 2 des deux côtés)
(soustrayez 2 des deux côtés) (diviser les deux côtés par 2)
(diviser les deux côtés par 2) (racine carrée des deux côtés ; rappelez-vous que la racine carrée donne des réponses possibles positives et négatives)
(racine carrée des deux côtés ; rappelez-vous que la racine carrée donne des réponses possibles positives et négatives)
6. Déterminer le domaine et l`étendue de la fonction inverse. Comme au début, examinez l`équation inversée pour déterminer le domaine et la plage. Avec deux solutions possibles, choisissez la solution qui a un domaine et une plage qui sont l`inverse du domaine et de la plage d`origine.
 . Comme la fonction racine carrée n`est pas définie pour les valeurs négatives, le terme . doit être
. Comme la fonction racine carrée n`est pas définie pour les valeurs négatives, le terme . doit être  toujours être positif. Par conséquent, les valeurs autorisées de x (le domaine) doivent être x≥2. Avec cela comme domaine, les valeurs résultantes de y (la plage) sont soit toutes les valeurs y≥0, si vous prenez la solution positive de la racine carrée, soit y≤0, si vous prenez la solution négative de la racine carrée. Notez que pour trouver la fonction inverse, vous avez initialement défini le domaine comme x≥0. Par conséquent, la solution correcte pour la fonction inverse est l`option positive.
toujours être positif. Par conséquent, les valeurs autorisées de x (le domaine) doivent être x≥2. Avec cela comme domaine, les valeurs résultantes de y (la plage) sont soit toutes les valeurs y≥0, si vous prenez la solution positive de la racine carrée, soit y≤0, si vous prenez la solution négative de la racine carrée. Notez que pour trouver la fonction inverse, vous avez initialement défini le domaine comme x≥0. Par conséquent, la solution correcte pour la fonction inverse est l`option positive. , le domaine a été défini comme toutes les valeurs de x≥0, et la plage a été définie comme toutes les valeurs de y≥2. Pour la fonction inverse, maintenant ces valeurs s`échangent, et le domaine est toutes les valeurs de x≥2, et la plage est toutes les valeurs de y≥0.
, le domaine a été défini comme toutes les valeurs de x≥0, et la plage a été définie comme toutes les valeurs de y≥2. Pour la fonction inverse, maintenant ces valeurs s`échangent, et le domaine est toutes les valeurs de x≥2, et la plage est toutes les valeurs de y≥0.
sept. Vérifiez si votre fonction inverse fonctionne. Pour vous assurer que votre travail est correct et que votre inverse est la bonne équation, choisissez n`importe quelle valeur pour x et placez-la dans l`équation d`origine pour trouver y. Ensuite, mettez cette valeur de y à la place de x dans votre équation inverse et voyez si vous obtenez le nombre avec lequel vous avez commencé. Si oui, ta fonction inverse est correcte.
 . Cela donne le résultat y=4.
. Cela donne le résultat y=4. . Cela donne en effet le résultat y=1. Vous pouvez conclure que votre fonction inverse est correcte.
. Cela donne en effet le résultat y=1. Vous pouvez conclure que votre fonction inverse est correcte.Méthode 2 sur 3: Compléter le carré pour trouver la fonction inverse

1. Donner à l`équation quadratique la forme correcte. Pour trouver l`inverse, il faut partir de l`équation de la forme  . Si nécessaire, vous devez combiner des termes similaires pour obtenir l`équation dans ce format. Avec l`équation écrite de cette façon, vous pouvez en dire un peu plus à ce sujet.
. Si nécessaire, vous devez combiner des termes similaires pour obtenir l`équation dans ce format. Avec l`équation écrite de cette façon, vous pouvez en dire un peu plus à ce sujet.
 . Si nécessaire, vous devez combiner des termes similaires pour obtenir l`équation dans ce format. Avec l`équation écrite de cette façon, vous pouvez en dire un peu plus à ce sujet.
. Si nécessaire, vous devez combiner des termes similaires pour obtenir l`équation dans ce format. Avec l`équation écrite de cette façon, vous pouvez en dire un peu plus à ce sujet. - La première chose que vous remarquerez est la valeur du coefficient a. si un>0, alors l`équation définit une parabole dont les extrémités pointent vers le haut (parabole de la vallée). si un<0, alors l`équation définit une parabole dont les extrémités pointent vers le bas (parabole de montagne). Notez que a≠0. Si ce n`était pas le cas, ce serait une fonction linéaire et non quadratique.

2. Reconnaître le format standard du quadratique. Avant de pouvoir trouver la fonction inverse, vous devez réécrire l`équation dans le format standard. Le format standard pour une fonction quadratique est  . Les termes numériques a, h et k seront évalués si vous transformez l`équation en calculant le carré.
. Les termes numériques a, h et k seront évalués si vous transformez l`équation en calculant le carré.
 . Les termes numériques a, h et k seront évalués si vous transformez l`équation en calculant le carré.
. Les termes numériques a, h et k seront évalués si vous transformez l`équation en calculant le carré. , qui est ensuite modifié par les deux autres éléments a et k. Pour arriver à cette forme quadratique parfaite, vous devrez créer certaines conditions dans votre équation quadratique.
, qui est ensuite modifié par les deux autres éléments a et k. Pour arriver à cette forme quadratique parfaite, vous devrez créer certaines conditions dans votre équation quadratique.
3. Repensez à la forme d`une fonction quadratique parfaite. Rappelons qu`une fonction quadratique qui est un carré parfait résulte de deux binômes de  , ou
, ou  . Si vous faites cette multiplication, vous obtenez
. Si vous faites cette multiplication, vous obtenez  . Ainsi le premier terme du quadratique est le premier terme du binôme, au carré, et le dernier terme du quadratique est le carré du deuxième terme du binôme. Le terme moyen est constitué de deux fois le produit des deux termes, dans ce cas
. Ainsi le premier terme du quadratique est le premier terme du binôme, au carré, et le dernier terme du quadratique est le carré du deuxième terme du binôme. Le terme moyen est constitué de deux fois le produit des deux termes, dans ce cas  .
.
 , ou
, ou  . Si vous faites cette multiplication, vous obtenez
. Si vous faites cette multiplication, vous obtenez  . Ainsi le premier terme du quadratique est le premier terme du binôme, au carré, et le dernier terme du quadratique est le carré du deuxième terme du binôme. Le terme moyen est constitué de deux fois le produit des deux termes, dans ce cas
. Ainsi le premier terme du quadratique est le premier terme du binôme, au carré, et le dernier terme du quadratique est le carré du deuxième terme du binôme. Le terme moyen est constitué de deux fois le produit des deux termes, dans ce cas  .
. et un deuxième terme x. A partir du coefficient de ce terme, que vous pouvez définir comme « 2b », vous devez obtenir
et un deuxième terme x. A partir du coefficient de ce terme, que vous pouvez définir comme « 2b », vous devez obtenir  voir pour trouver. Cela nécessite une combinaison de division par deux puis de quadrature de ce résultat.
voir pour trouver. Cela nécessite une combinaison de division par deux puis de quadrature de ce résultat.
4. Assurez-vous que le coefficient de X 2  1 est. Vous souvenez-vous de la forme originale de la fonction quadratique
1 est. Vous souvenez-vous de la forme originale de la fonction quadratique  . Si le premier coefficient est autre que 1, alors vous devez diviser tous les termes par cette valeur pour obtenir a=1.
. Si le premier coefficient est autre que 1, alors vous devez diviser tous les termes par cette valeur pour obtenir a=1.
 1 est. Vous souvenez-vous de la forme originale de la fonction quadratique
1 est. Vous souvenez-vous de la forme originale de la fonction quadratique  . Si le premier coefficient est autre que 1, alors vous devez diviser tous les termes par cette valeur pour obtenir a=1.
. Si le premier coefficient est autre que 1, alors vous devez diviser tous les termes par cette valeur pour obtenir a=1. . Vous pouvez simplifier cela en divisant tous les termes par 2 pour obtenir la fonction résultante
. Vous pouvez simplifier cela en divisant tous les termes par 2 pour obtenir la fonction résultante  pour obtenir. Le coefficient 2 reste en dehors des parenthèses et fera partie de votre solution finale.
pour obtenir. Le coefficient 2 reste en dehors des parenthèses et fera partie de votre solution finale. sera simplifié pour
sera simplifié pour  . Travaillez soigneusement les fractions.
. Travaillez soigneusement les fractions.
5. Trouver la moitié du coefficient du milieu et le carré. Vous avez déjà les deux premiers termes de la formule quadratique. Ce sont le terme  et le coefficient qui représente le terme x. En prenant ce coefficient comme valeur, vous pouvez ajouter ou soustraire le nombre nécessaire pour faire un carré parfait. Rappelons ci-dessus que le troisième terme requis du carré est ce deuxième coefficient divisé par deux, puis au carré.
et le coefficient qui représente le terme x. En prenant ce coefficient comme valeur, vous pouvez ajouter ou soustraire le nombre nécessaire pour faire un carré parfait. Rappelons ci-dessus que le troisième terme requis du carré est ce deuxième coefficient divisé par deux, puis au carré.
 et le coefficient qui représente le terme x. En prenant ce coefficient comme valeur, vous pouvez ajouter ou soustraire le nombre nécessaire pour faire un carré parfait. Rappelons ci-dessus que le troisième terme requis du carré est ce deuxième coefficient divisé par deux, puis au carré.
et le coefficient qui représente le terme x. En prenant ce coefficient comme valeur, vous pouvez ajouter ou soustraire le nombre nécessaire pour faire un carré parfait. Rappelons ci-dessus que le troisième terme requis du carré est ce deuxième coefficient divisé par deux, puis au carré. vous trouvez le troisième terme nécessaire en divisant 3 par 2 (ou 3/2), puis en le carré, pour obtenir 9/4. Le quadratique
vous trouvez le troisième terme nécessaire en divisant 3 par 2 (ou 3/2), puis en le carré, pour obtenir 9/4. Le quadratique  est un carré parfait.
est un carré parfait. sont. La moitié du moyen terme est -2, puis vous le carré pour obtenir 4. Le carré parfait résultant est
sont. La moitié du moyen terme est -2, puis vous le carré pour obtenir 4. Le carré parfait résultant est  .
.
6. Ajouter et soustraire du troisième terme requis en même temps. C`est un concept délicat, mais ça marche. Ajouter et soustraire le même nombre à différents endroits de votre fonction ne change pas vraiment la valeur de la fonction. Cependant, en faisant cela, vous obtiendrez votre fonction sous une forme appropriée.
 . Comme mentionné ci-dessus, vous utilisez les deux premiers termes pour compléter le carré. En utilisant le terme moyen de -4x, vous générez un troisième terme +4. Ajouter 4 et soustraire 4 de l`équation, sous la forme
. Comme mentionné ci-dessus, vous utilisez les deux premiers termes pour compléter le carré. En utilisant le terme moyen de -4x, vous générez un troisième terme +4. Ajouter 4 et soustraire 4 de l`équation, sous la forme  . Les parenthèses ne sont placées que pour définir l`équation quadratique que vous faites. Notez le +4 à l`intérieur des crochets et le -4 à l`extérieur. Simplifier les nombres au résultat
. Les parenthèses ne sont placées que pour définir l`équation quadratique que vous faites. Notez le +4 à l`intérieur des crochets et le -4 à l`extérieur. Simplifier les nombres au résultat  .
.
sept. Factoriser l`équation quadratique. Le polynôme entre parenthèses est une équation quadratique, que vous pouvez réécrire sous la forme  . Dans l`exemple de l`étape précédente (
. Dans l`exemple de l`étape précédente ( ) vous factorisez le facteur quadratique dans
) vous factorisez le facteur quadratique dans  . Copiez le reste de l`équation pour que votre solution
. Copiez le reste de l`équation pour que votre solution  devient. C`est la même fonction que votre équation quadratique d`origine (
devient. C`est la même fonction que votre équation quadratique d`origine ( ), réécrit sous la forme standard
), réécrit sous la forme standard  .
.
 . Dans l`exemple de l`étape précédente (
. Dans l`exemple de l`étape précédente ( ) vous factorisez le facteur quadratique dans
) vous factorisez le facteur quadratique dans  . Copiez le reste de l`équation pour que votre solution
. Copiez le reste de l`équation pour que votre solution  devient. C`est la même fonction que votre équation quadratique d`origine (
devient. C`est la même fonction que votre équation quadratique d`origine ( ), réécrit sous la forme standard
), réécrit sous la forme standard  .
.
8. Définir le domaine et la portée de la fonction. Le domaine est l`ensemble des valeurs x qui peuvent être utilisées comme entrées de la fonction. La plage est l`ensemble des valeurs y qui peuvent être le résultat. Rappelons qu`une parabole n`est pas une fonction avec un inverse définissable, car il n`y a pas de relation biunivoque entre les valeurs x et les valeurs y, en raison de la symétrie de la parabole. Pour résoudre ce problème, vous devez définir le domaine comme toutes les valeurs de x supérieures à x=h, le sommet de la parabole.
 . Comme il s`agit d`un format standard, vous pouvez déterminer le sommet sous la forme x=2, y=5. Donc, pour éviter la symétrie, vous ne travaillez qu`avec le côté droit du graphique et définissez le domaine si toutes les valeurs x≥2. L`insertion de la valeur x=2 dans la fonction renvoie y=5. Vous pouvez voir que les valeurs de y augmenteront à mesure que x augmente. Par conséquent, l`étendue de cette équation est y≥5.
. Comme il s`agit d`un format standard, vous pouvez déterminer le sommet sous la forme x=2, y=5. Donc, pour éviter la symétrie, vous ne travaillez qu`avec le côté droit du graphique et définissez le domaine si toutes les valeurs x≥2. L`insertion de la valeur x=2 dans la fonction renvoie y=5. Vous pouvez voir que les valeurs de y augmenteront à mesure que x augmente. Par conséquent, l`étendue de cette équation est y≥5.
9. Échanger les valeurs x et y. C`est l`étape où vous commencez par trouver la forme inverse de l`équation. Laissez l`équation dans son intégralité sauf en échangeant ces variables.
 . Insérez x à la place de f(x) et insérez y (ou f(x), si vous préférez) à la place de x. Cela donne comme nouvelle fonction
. Insérez x à la place de f(x) et insérez y (ou f(x), si vous préférez) à la place de x. Cela donne comme nouvelle fonction  .
.
dix. Réécrire l`équation inverse en fonction de y. En utilisant une combinaison d`étapes algébriques, en vous assurant d`effectuer la même opération uniformément des deux côtés de l`équation, isolez la variable y. Pour la comparaison de travail  cette révision ressemble à ceci :
cette révision ressemble à ceci :
 cette révision ressemble à ceci :
cette révision ressemble à ceci : (point de départ initial)
(point de départ initial) (soustrayez 5 des deux côtés)
(soustrayez 5 des deux côtés) (racine carrée des deux côtés ; rappelez-vous que la racine carrée donne des réponses possibles positives et négatives)
(racine carrée des deux côtés ; rappelez-vous que la racine carrée donne des réponses possibles positives et négatives) (ajouter 2 des deux côtés)
(ajouter 2 des deux côtés)
11. Déterminer le domaine et l`étendue de la fonction inverse. Comme au début, examinez l`équation inverse pour déterminer le domaine et la plage. Avec deux solutions possibles, choisissez la solution qui a un domaine et une plage qui sont l`inverse du domaine et de la plage d`origine.
 . Comme la fonction racine carrée n`est pas définie pour les valeurs négatives, le terme . doit être
. Comme la fonction racine carrée n`est pas définie pour les valeurs négatives, le terme . doit être  toujours être positif. Par conséquent, les valeurs autorisées de x (le domaine) doivent être x≥5. Avec cela comme domaine, les valeurs résultantes de y (la plage) sont soit toutes les valeurs y≥2 (si vous prenez la solution positive de la racine carrée), soit y≤2 (si vous choisissez la solution négative de la racine carrée). Rappelez-vous que vous avez initialement défini le domaine comme x≥2, afin de trouver la fonction inverse. Par conséquent, la solution correcte pour la fonction inverse est l`option positive.
toujours être positif. Par conséquent, les valeurs autorisées de x (le domaine) doivent être x≥5. Avec cela comme domaine, les valeurs résultantes de y (la plage) sont soit toutes les valeurs y≥2 (si vous prenez la solution positive de la racine carrée), soit y≤2 (si vous choisissez la solution négative de la racine carrée). Rappelez-vous que vous avez initialement défini le domaine comme x≥2, afin de trouver la fonction inverse. Par conséquent, la solution correcte pour la fonction inverse est l`option positive.
12. Vérifiez si votre fonction inverse fonctionne. Pour vous assurer que votre travail est correct et que votre inverse est la bonne équation, choisissez n`importe quelle valeur pour x et placez-la dans l`équation d`origine pour trouver y. Ensuite, mettez cette valeur de y à la place de x dans votre équation inverse et voyez si vous obtenez le nombre avec lequel vous avez commencé. Si oui, alors votre fonction inverse est correcte.
 procéder. Cela donne le résultat y=6.
procéder. Cela donne le résultat y=6. . Cela renvoie y=3, qui est le nombre avec lequel vous avez commencé. Vous pouvez conclure que votre fonction inverse est correcte.
. Cela renvoie y=3, qui est le nombre avec lequel vous avez commencé. Vous pouvez conclure que votre fonction inverse est correcte.Méthode 3 sur 3: Utilisation de la formule carrée

1. Utiliser la formule quadratique pour résoudre x. N`oubliez pas que lors de la résolution d`équations quadratiques, il existe une méthode pour les factoriser (si possible). Si la factorisation ne fonctionnait pas, vous pourriez utiliser la formule carrée, qui donnerait les vraies solutions à n`importe quelle équation quadratique. Vous pouvez également utiliser la formule carrée comme méthode pour trouver des fonctions inverses.
- La formule carrée est x=[-b±√(b^2-4ac)]/2a.
- Notez que la formule carrée donne deux solutions possibles, une positive et une négative. Vous ferez ce choix en fonction de la détermination du domaine et de la portée de la fonction.

2. Commencer par une équation quadratique pour trouver l`inverse. Votre équation quadratique doit commencer dans le format  . Suivez les étapes algébriques nécessaires pour obtenir votre équation sous cette forme.
. Suivez les étapes algébriques nécessaires pour obtenir votre équation sous cette forme.
 . Suivez les étapes algébriques nécessaires pour obtenir votre équation sous cette forme.
. Suivez les étapes algébriques nécessaires pour obtenir votre équation sous cette forme. .
.
3. Tracer l`équation pour déterminer le domaine et la plage. Représentez graphiquement la fonction, soit à l`aide d`une calculatrice graphique, soit en traçant plusieurs points jusqu`à ce que vous puissiez tracer la parabole. Vous verrez que cette équation définit une parabole avec le point le plus élevé à (-1,-4). Donc, pour définir cela comme une fonction qui aura un inverse, vous définissez le domaine comme toutes les valeurs de x≤-1. La plage est alors toutes les valeurs y≥-4.

4. Échanger les variables x et y. Pour trouver l`inverse, échangez les variables x et y. Laisser l`équation inchangée, sauf échanger les variables. A ce stade, remplacez x par f(x).
 , est-ce que cela donne le résultat
, est-ce que cela donne le résultat  .
.
5. Mettre le côté gauche de l`équation égal à zéro. N`oubliez pas que pour utiliser la formule quadratique, vous devez définir l`équation égale à zéro, puis utilisez les coefficients de la formule. De même, cette méthode de recherche d`une fonction inverse commence par définir l`équation égale à zéro.
 .
.
6. Redéfinir les variables pour s`adapter à la formule carrée. Cette étape est un peu délicate. Sachez que la formule carrée résout pour x, dans l`équation  . Donc, pour l`équation que vous avez maintenant,
. Donc, pour l`équation que vous avez maintenant,  , pour vous conformer à cette classification, vous devez redéfinir les termes comme suit :
, pour vous conformer à cette classification, vous devez redéfinir les termes comme suit :
 . Donc, pour l`équation que vous avez maintenant,
. Donc, pour l`équation que vous avez maintenant,  , pour vous conformer à cette classification, vous devez redéfinir les termes comme suit :
, pour vous conformer à cette classification, vous devez redéfinir les termes comme suit : . Donc, x=1
. Donc, x=1 . Donc, b=2
. Donc, b=2 . Donc, c=(-3-x)
. Donc, c=(-3-x)
sept. Résoudre la formule carrée avec ces valeurs redéfinies. Normalement, vous traiteriez les valeurs de a, b et c dans la formule carrée pour résoudre x. Cependant, rappelez-vous que vous avez précédemment échangé x et y pour trouver la fonction inverse. Ainsi, lorsque vous utilisez la formule carrée pour résoudre x, vous résolvez en fait y, ou l`inverse de f. Les étapes de résolution de la formule carrée fonctionnent comme suit :

8. Notez les deux solutions possibles. Notez que la formule carrée donne deux résultats possibles, en utilisant le symbole ±. Écrivez les deux solutions distinctes pour faciliter la détermination du domaine et de la plage et donner la bonne solution finale. Ces deux solutions sont :



9. Déterminer le domaine et l`étendue de la fonction inverse. Notez que pour définir la racine carrée, le domaine doit être x≥-4. Rappelons que le domaine de la fonction d`origine était x≤-1 et la plage était y≥-4. Pour choisir la fonction inverse qui correspond, vous avez besoin de la deuxième solution,  choisir comme fonction inverse correcte.
choisir comme fonction inverse correcte.
 choisir comme fonction inverse correcte.
choisir comme fonction inverse correcte.
dix. Vérifiez si votre fonction inverse est correcte. Pour vous assurer que votre travail est correct et que votre inverse est la bonne équation, choisissez n`importe quelle valeur pour x et placez-la dans l`équation d`origine pour trouver y. Ensuite, mettez cette valeur de y à la place de x dans votre équation inverse et voyez si vous obtenez le nombre avec lequel vous avez commencé. Si oui, alors votre fonction inverse est correcte.
 , choisissez votre x=-2. Cela renvoie y=-3. Remplacez maintenant la valeur de x=-3 dans la fonction inverse,
, choisissez votre x=-2. Cela renvoie y=-3. Remplacez maintenant la valeur de x=-3 dans la fonction inverse,  . Cela renvoie -2, qui est bien la valeur avec laquelle vous avez commencé. Donc ta définition de la fonction inverse est correcte.
. Cela renvoie -2, qui est bien la valeur avec laquelle vous avez commencé. Donc ta définition de la fonction inverse est correcte.Articles sur le sujet "Trouver l'inverse d'une équation quadratique"
Оцените, пожалуйста статью
Populaire