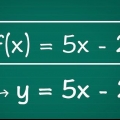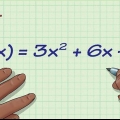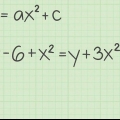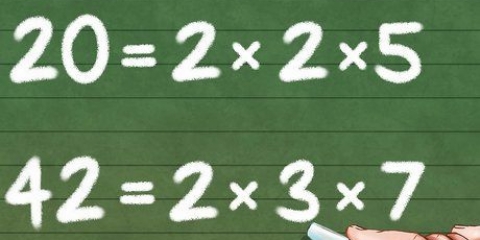Un polynôme sans racines ni fractions avec des variables au dénominateur. Le domaine de ce type de fonction est constitué de l`ensemble de tous les nombres réels. Une fonction avec une fraction avec une variable au dénominateur. Pour trouver le domaine de ce type de fonction, définissez le dénominateur de la fraction égal à zéro et ignorez la valeur x que vous trouvez après avoir résolu l`équation. Une fonction avec une variable à l`intérieur d`un radical. Pour trouver le domaine de ce type de fonction, définissez les termes dans le radical supérieur à 0 et résolvez l`équation pour savoir quelles valeurs pour x sont correctes dans cette fonction. Une fonction avec un logarithme népérien (ln). Mettre les termes entre parenthèses >0 et résoudre. Un graphique. Déduire du graphique quelles valeurs sont correctes pour x. Une relation. Ceci est une liste de coordonnées x et y. Votre domaine est simplement une liste de coordonnées x. 
La structure d`un domaine est une accolade ouverte, suivie des 2 extrémités du domaine séparées par une virgule et suivies d`une accolade fermante. Par exemple : [-1.5). Cela signifie que le domaine passe de -1 à 5. Utilisez des crochets comme [ et ] pour indiquer si un nombre appartient à un certain domaine. Donc dans l`exemple, [-1.5), -1 tombe dans le domaine. Utilisez des parenthèses comme ( et ) pour indiquer qu`un numéro est en dehors d`un certain domaine. Donc dans l`exemple, [-1.5), le 5 est en dehors du domaine. Le domaine s`arrête à n`importe quel point avant le 5, par exemple 4 999… Utilisez « U » (ce qui signifie "syndicat") pour connecter des parties du domaine qui sont séparées les unes des autres.` Par exemple : [-1,5) U (5,10]. Cela signifie que le domaine passe de -1 à 10, mais il y a un écart dans le domaine à 5. Par exemple, cela pourrait être dû à une fonction avec "x - 5" dans le dénominateur. tu peux faire tellement "VOUS"-utiliser des symboles si nécessaire, si le domaine a plusieurs ruptures. Utilisez le symbole de l`infini (dans les directions positive et négative) pour indiquer que dans cette direction le domaine est l`infini. À l`infini, utilisez toujours ( ) et non [ ]. 

f(x) = 2x/(x - 4) x - 4 = 0 (x - 2 )(x + 2) = 0 x (2, - 2) 
x = tous les nombres réels sauf 2 et -2 

x-7 0 
x 7 
D = [7,∞) 
Vérifiez maintenant la zone ci-dessous -2 (par ex. -3), si cela donne un résultat supérieur à zéro. C`est vrai. (-3) - 4 = 5 Vérifiez maintenant la zone entre -2 et 2. Par exemple, prenez 0. 0 - 4 = -4, donc vous savez que les nombres entre -2 et 2 ne fonctionnent pas. Essayez maintenant un nombre supérieur à 2, tel que +3. 3 - 4 = 5, donc les nombres au-dessus de 2 fonctionnent. Notez le domaine lorsque vous avez terminé. Voici comment l`écrire : D = (-∞, -2) U (2, ) 

x - 8 > 0 
x - 8 + 8 > 0 + 8 X > 8 
D = (8,∞) 

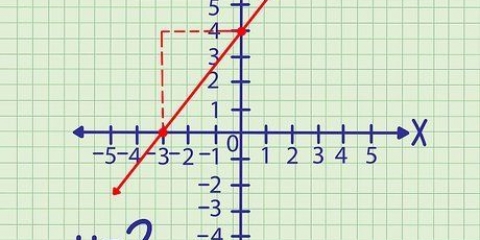
Une ligne. Si vous voyez une ligne sur le graphique allant à l`infini, finalement chaque valeur x sera contenue dans la parabole, donc le domaine est égal à tous les nombres réels. Une parabole ordinaire. Si vous voyez une parabole pointant vers le haut ou vers le bas, alors le domaine se compose de tous les nombres réels, car tous les nombres sur l`axe des x sont finalement contenus dans la parabole. Une parabole horizontale. Si vous avez affaire à une parabole dont le sommet en (4,0) s`étend infiniment vers la droite, alors votre domaine est égal à D = [4,∞) 




Trouver le domaine d'une fonction
Teneur
- Pas
- Méthode 1 sur 6: Apprendre les bases
- Méthode 2 sur 6: Trouver le domaine d`une fonction qui contient une fraction
- Méthode 3 sur 6: Trouver le domaine d`une fonction avec une racine carrée
- Méthode 4 sur 6: Trouver le domaine d`une fonction à l`aide du logarithme népérien
- Méthode 5 sur 6: Trouver le domaine d`une fonction à l`aide d`un graphique
- Méthode 6 sur 6 : Détermination du domaine d`une fonction à l`aide d`une collection/relation
Le domaine d`une fonction est une collection de nombres qui rentrent dans cette fonction. En d`autres termes, c`est une collection de valeurs x associées à une équation donnée. L`ensemble des valeurs y est appelé gamme de fonction. Si vous souhaitez savoir comment trouver le domaine d`une fonction dans différentes situations, suivez ces étapes.
Pas
Méthode 1 sur 6: Apprendre les bases

1. Apprendre la définition d`un domaine. Un domaine d`une fonction est défini comme l`ensemble de tous les nombres réels qui peuvent servir d`entrées à cette fonction. En d`autres termes, un domaine est l`ensemble complet de valeurs x entrées dans une fonction, ce qui donne un ensemble de valeurs y.

2. Apprenez à trouver le domaine des différentes fonctions. Le type de fonctionnalité déterminera la meilleure méthode pour trouver un domaine. Voici les bases dont vous aurez besoin pour les fonctions suivantes :

3. Comprendre la notation d`un domaine. La notation correcte d`un domaine est facile à apprendre, mais il est important que vous le fassiez correctement afin de ne pas manquer des points dans les tests et examens. Voici quelques éléments que vous devez savoir pour écrire correctement le domaine d`une fonction :
Méthode 2 sur 6: Trouver le domaine d`une fonction qui contient une fraction

1. Ecrire le devoir. Supposons que vous ayez le problème suivant :
- f(x) = 2x/(x - 4)

2. Pour les fractions avec une variable au dénominateur, vous définissez cette variable égale à zéro dans une équation. Si vous voulez trouver le domaine d`une fonction avec une fraction, excluez toutes les valeurs x qui rendent le dénominateur égal à zéro, car vous ne pouvez jamais diviser par zéro. Écrivez donc le dénominateur sous forme d`équation et mettez-le égal à 0. Voici comment procéder :

3. Notez le domaine. Voici comment procéder :
Méthode 3 sur 6: Trouver le domaine d`une fonction avec une racine carrée

1. Ecrire le devoir. Supposons que vous ayez le problème suivant : Y = (x-7)

2. Assurez-vous que les termes dans la racine carrée peuvent être supérieurs ou égaux à 0. Vous ne pouvez pas prendre la racine carrée d`un nombre négatif, mais vous pouvez prendre la racine carrée de zéro. Notez que cela s`applique non seulement aux racines carrées, mais à tous les nombres de racines paires. Il ne s`applique pas aux nombres radicaux impairs, car ce n`est pas un problème s`il y a un nombre négatif sous le signe radical. Voici un exemple :

3. Isoler la variable. Maintenant, pour séparer x sur le côté gauche de l`équation, ajoutez 7 aux deux côtés du signe égal, de sorte qu`après cette opération, cela ressemblera à ceci :

4. Notez le domaine correctement. C`est la notation correcte :

5. Trouver le domaine d`une fonction avec une racine carrée si plusieurs solutions sont possibles. Supposons que vous ayez la fonction suivante : y = 1/√( ̅x -4). Si vous prenez le dénominateur en dehors des parenthèses et le rendez égal à zéro, vous obtenez x ≠ (2, - 2). Voici comment procéder :
Méthode 4 sur 6: Trouver le domaine d`une fonction à l`aide du logarithme népérien

1. Ecrire le devoir. Supposons que vous ayez ceci :
- f(x) = ln(x-8)

2. Rendre les termes entre parenthèses supérieurs à zéro. Le logarithme népérien doit être positif, alors rendez les termes entre parenthèses supérieurs à zéro. Voici un exemple :

3. Résoudre. Séparez la variable x en ajoutant 8 des deux côtés de l`équation. Voici comment:

4. Notez le domaine. Montrer que le domaine de cette équation est égal à tous les nombres supérieurs à 8 à l`infini. Voici comment:
Méthode 5 sur 6: Trouver le domaine d`une fonction à l`aide d`un graphique

1. Voir le graphique.

2. Enquêter sur les valeurs x appartenant au graphique. C`est plus facile à dire qu`à faire, voici donc quelques conseils :

3. Déterminer le domaine. Déterminez le domaine en fonction du type de graphique que vous avez. Si vous n`êtes pas tout à fait sûr mais que vous connaissez l`équation de la ligne, entrez les coordonnées x dans la fonction pour vérifier.
Méthode 6 sur 6 : Détermination du domaine d`une fonction à l`aide d`une collection/relation

1. Écrivez la relation. Une relation est simplement une série de coordonnées x et y. Supposons que vous ayez les coordonnées suivantes : {(1, 3), (2, 4), (5, 7)}

2. Notez les coordonnées x. Ce sont : 1, 2, 5.

3. Déterminer le domaine. D = {1, 2, 5}

4. Assurez-vous que cette relation est une fonction. Une relation est une fonction si chaque fois que vous entrez une coordonnée x numérique, vous obtenez la même coordonnée y comme réponse. Donc, si vous mettez un 3 devant le x, vous obtenez 6 comme valeur y, et ainsi de suite. La prochaine relation est ne pas une fonction car vous obtenez deux valeurs y différentes pour chaque valeur de "X": {(1, 4),(3, 5),(1, 5)}.
Articles sur le sujet "Trouver le domaine d'une fonction"
Оцените, пожалуйста статью
Similaire
Populaire