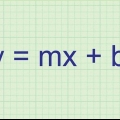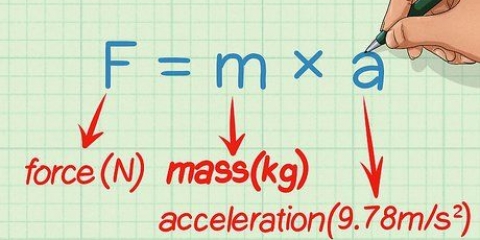Déterminer la portée d'une fonction

Teneur

Pas
Des astuces

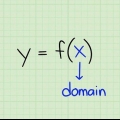
La plage d`une fonction est l`ensemble des nombres que la fonction peut produire. En d`autres termes, c`est l`ensemble des valeurs y que vous obtenez lorsque vous factorisez toutes les valeurs x possibles dans la fonction. Cet ensemble de valeurs x est appelé le domaine. Si vous voulez savoir comment calculer la plage d`une fonction, suivez les étapes ci-dessous.

Pas

Méthode 1 sur 4: Détermination de la plage d`une fonction avec une équation donnée

Image intitulée Trouver la plage d`une fonction dans Math Step 1

1. Écrivez l`équation. Supposons que vous ayez l`équation suivante : f(x) = 3x + 6x -2. Cela signifie que lorsque vous entrez une valeur pour le X de l`équation, que vous avez alors un oui-obtient de la valeur. C`est la fonction d`une parabole.

Image intitulée Trouver la plage d`une fonction dans Math Step 2

2. Trouver le sommet de la fonction, si c`est une équation quadratique. Si vous avez une ligne droite ou une fonction avec un polynôme ou un nombre impair, comme f(x) = 6x+2x + 7, vous pouvez sauter cette étape. Mais si vous avez affaire à une parabole ou à une équation où la coordonnée x est au carré ou augmentée d`une puissance paire, vous devrez tracer le sommet de la parabole. Pour ce faire, utilisez l`équation -b/2a pour la coordonnée x de la fonction 3x + 6x -2, où 3 = a, 6 = b et -2 = c. Dans ce cas, -b est de -6 et 2a est 6, donc la coordonnée x est -6/6, ou -1.

Ensuite, traitez -1 dans la fonction pour obtenir la coordonnée y. f(-1) = 3(-1) + 6(-1) -2 = 3 - 6 -2 = -5.

Le sommet de la parabole est (-1,-5). Traitez cela dans le graphique en dessinant un point à la coordonnée x -1 et à la coordonnée y -5. Cela devrait être dans le troisième quadrant du graphique.

Image intitulée Trouver la plage d`une fonction dans Math Step 3

3. Trouver d`autres points de la fonction. Pour avoir une idée de la fonction, vous devez remplir d`autres valeurs pour x afin que vous puissiez avoir une idée de ce à quoi ressemble la fonction avant de commencer à rechercher la plage. Puisqu`il s`agit d`une parabole et que x est positif, la parabole pointera vers le haut (parabole de la vallée). Mais juste pour être sûr, nous entrons quelques valeurs supplémentaires pour x pour voir quelles coordonnées y elles donnent :

f(-2) = 3(-2) + 6(-2) -2 = -2. Un point sur le graphique est (-2, -2)

f(0) = 3(0) + 6(0) -2 = -2. Un autre point sur le graphique est (0,-2)

f(1) = 3(1) + 6(1) -2 = 7. Un troisième point sur le graphique est (1, 7).

Image intitulée Trouver la plage d`une fonction dans Math Step 4

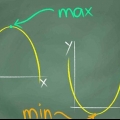
4. Trouver la portée du graphique. Maintenant, regardez les coordonnées y sur le graphique et trouvez le point le plus bas où le graphique touche la coordonnée y. Dans ce cas, la coordonnée y la plus basse est au sommet de la parabole, -5 et le graphique s`étend infiniment au-delà de ce point. Cela signifie que la plage de la fonction y = tous les nombres réels ≥ -5.

Méthode 2 sur 4: Détermination de la plage d`une fonction à l`aide d`un graphique

Image intitulée Trouver la plage d`une fonction dans Math Step 5

1. Trouver le minimum de la fonction. Trouver la plus petite coordonnée y de la fonction. Supposons que la fonction atteigne son point le plus bas à -3. Cette fonction peut devenir de plus en plus petite, jusqu`à l`infini, elle n`a donc pas de point le plus bas fixe - juste l`infini.

Image intitulée Trouver la plage d`une fonction dans Math Step 6

2. Trouver le maximum de la fonction. Supposons que la plus haute coordonnée y de la fonction est 10. Cette fonction peut également devenir infiniment plus grande, elle n`a donc pas de point le plus élevé fixe - juste infini.

Image intitulée Trouver la plage d`une fonction dans Math Step 7

3. Indiquez quelle est la plage. Cela signifie que la plage de la fonction, ou la plage des coordonnées y, est de -3 à 10. Donc, -3 f(x) ≤ 10. C`est la portée de la fonction.

Mais supposons que y = -3 soit le point le plus bas du graphique , mais augmente pour toujours. Alors la plage est f(x) -3, et pas plus que cela.

Supposons que le graphique atteigne son point le plus élevé à y = 10, mais continue ensuite à baisser pour toujours. Alors la plage est f(x) ≤ 10.

Méthode 3 sur 4: Déterminer la portée de la fonction d`une relation

Image intitulée Trouver la plage d`une fonction dans Math Step 8

1. Écrivez la relation. Une relation est un ensemble de paires ordonnées de coordonnées x et y. Vous pouvez examiner une relation et déterminer son domaine et sa portée. Supposons que vous ayez affaire à la relation suivante : {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}.

Image intitulée Trouver la plage d`une fonction dans Math Step 9

2. Lister les coordonnées y de la relation. Pour déterminer l`étendue de la relation, nous écrivons toutes les coordonnées y de chaque paire ordonnée : {-3, 6, -1, 6, 3}.

Image intitulée Trouver la plage d`une fonction dans Math Step 10

3. Supprimez toutes les coordonnées en double afin que vous n`ayez qu`une seule de chaque coordonnée y. Vous avez peut-être remarqué que vous avez le "6" deux fois dans la liste. Supprimez-le pour vous retrouver avec {-3, -1, 6, 3}.

Image intitulée Trouver la plage d`une fonction dans Math Step 11

4. Écrivez la plage de la relation dans l`ordre croissant. Ensuite, organisez les nombres dans l`ensemble du plus petit au plus grand, et vous avez trouvé la plage. La plage de la relation {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} est {-3,-1, 3, 6}. Vous êtes prêt.

Image intitulée Trouver la plage d`une fonction dans Math Step 12

5. Faire de la relation une fonction est. Pour qu`une relation soit une fonction, chaque fois que vous entrez un nombre à partir d`une coordonnée x, la coordonnée y doit être la même. Par exemple, la relation {(2, 3) (2, 4) (6, 9)} est non fonction, car si vous remplissez le 2 comme x pour la première fois, vous obtenez un 3 comme valeur, mais la deuxième fois que vous remplissez un 2, vous obtenez quatre. Une relation n`est une fonction que si vous obtenez toujours la même sortie pour une certaine entrée. Si vous entrez -7, vous devriez toujours obtenir la même coordonnée y (quelle qu`elle soit), à chaque fois.

Méthode 4 sur 4: Déterminer la portée d`une fonction dans un problème

Image intitulée Trouver la plage d`une fonction dans Math Step 13

1. Lire le numéro. Supposons que vous travaillez sur le problème suivant : "Becky vend des billets pour le spectacle de talents de son école à 5 $ chacun. Le montant total qu`elle récolte est fonction du nombre de billets qu`elle vend. Quelle est la portée de la fonction?"

Image intitulée Trouver la plage d`une fonction dans Math Step 14

2. Écrire le problème sous forme de fonction. Dans ce cas m le montant qui a été perçu et t le nombre de billets vendus. Puisque chaque billet coûte 5 euros, vous devrez multiplier le nombre de billets vendus par 5 pour obtenir le montant total. Par conséquent, la fonction peut être écrite comme M(t) = 5t.

Par exemple : Si elle vend 2 tickets vous devrez multiplier 2 par 5, avec 10 comme réponse, et donc le montant total récolté.

Image intitulée Trouver la plage d`une fonction dans Math Step 15

3. Déterminer quel est le domaine. Pour trouver la gamme, vous avez d`abord besoin du domaine. Le domaine se compose de toutes les valeurs possibles de t qui participent à l`équation. Dans ce cas, Becky peut vendre 0 ou plusieurs billets - elle ne peut pas vendre un nombre négatif de billets. Comme on ne connaît pas le nombre de places dans l`auditorium de l`école, on peut supposer qu`elle peut en théorie vendre un nombre infini de billets. Et elle ne peut vendre que des billets entiers, pas une partie d`entre eux. Par conséquent, le domaine de la fonction t = tout entier positif.

Image intitulée Trouver la plage d`une fonction dans Math Step 16

4. Déterminer quelle est la plage. La fourchette est le montant possible que Becky peut collecter avec la vente. Vous devrez travailler avec le domaine pour trouver la gamme. Si vous savez que le domaine est constitué d`un entier positif et que l`équation M(t) = 5t alors vous savez également que vous pouvez entrer n`importe quel entier positif dans cette fonction pour la réponse ou la plage. Par exemple : Si elle vend 5 billets, alors M(5) = 5 x 5, soit 25 euros. Si elle en vend 100, alors M(100) = 5 x 100, soit 500 euros. Par conséquent, la portée de la fonction tout entier positif qui est un multiple de cinq.

Autrement dit, tout entier positif qui est un multiple de cinq est un résultat possible de la fonction.

Des astuces

Voyez si vous pouvez trouver l`inverse de la fonction. Le domaine de l`inverse d`une fonction est égal à l`étendue de cette fonction.
Dans les cas les plus difficiles, il peut être plus facile de tracer d`abord le graphique en utilisant le domaine (si nécessaire), puis de lire la plage à partir du graphique.
Vérifiez si la fonction se répète. Toute fonction qui se répète le long de l`axe des x aura la même plage pour l`ensemble de la fonction. Par exemple : f(x) = sin(x) a une plage comprise entre -1 et 1.