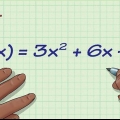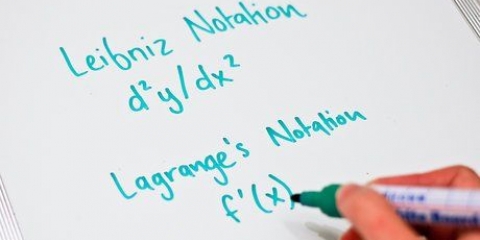Détermination des valeurs maximales et minimales d'une fonction carrée

Teneur

Pas
Des astuces

La coordonnée y de la crête ou de la vallée d`une parabole (généralement représentée par k) est également la valeur maximale ou minimale de l`équation quadratique représentée par la parabole. Voyons comment le déterminer!

Pas

Méthode 1 sur 4: Pour une équation quadratique de la forme y = ax + bx + c

Image intitulée Trouvez facilement la valeur maximale ou minimale d`une fonction quadratique Étape 1

1. Décidez si vous voulez déterminer la valeur maximale ou la valeur minimale. C`est l`un ou l`autre, tu ne peux pas faire les deux.

La valeur maximale ou minimale d`une équation quadratique est la même que le pic ou la vallée de cette fonction.
La fonction y = ax + bx + c,
(c - b/4a) renvoie la valeur y (la valeur de la fonction) comme sommet.

Image intitulée Trouvez facilement la valeur maximale ou minimale d`une fonction quadratique Étape 1Bullet1

Si la valeur de une est positif, alors vous obtenez la valeur minimale, car la parabole du haut est ouverte (le sommet est le point le plus bas du graphique).

Image intitulée Trouvez facilement la valeur maximale ou minimale d`une fonction quadratique Étape 1Bullet2

Si la valeur de une est négatif, vous trouverez la valeur maximale, car la parabole du bas est ouverte (le sommet est le point le plus haut du graphique).

Image intitulée Trouvez facilement la valeur maximale ou minimale d`une fonction quadratique Étape 1Bullet3

La valeur de une ne peut pas être zéro, sinon nous n`avons pas affaire à une équation quadratique, n`est-ce pas?

Image intitulée Trouvez facilement la valeur maximale ou minimale d`une fonction quadratique Étape 1Bullet4

Méthode 2 sur 4: Pour une équation quadratique sous la forme y = a(x-h) + k

Image intitulée Trouvez facilement la valeur maximale ou minimale d`une fonction quadratique Étape 2

1. Pour y = a(x-h) + k, k est la valeur de la fonction au sommet.

k nous donne la valeur maximale ou minimale de l`équation quadratique lorsque une est respectivement négatif ou positif.

Image intitulée Trouvez facilement la valeur maximale ou minimale d`une fonction quadratique Étape 2Bullet1

Méthode 3 sur 4: Différencier sur une équation quadratique de la forme y = ax^2 + bx + c

Image intitulée Trouvez facilement la valeur maximale ou minimale d`une fonction quadratique Étape 3

1. Différencier y pour x. dy/dx = 2ax + b

Image intitulée Trouvez facilement la valeur maximale ou minimale d`une fonction quadratique Étape 4

2. Déterminer quelles sont les valeurs dérivées en termes de dy/dx. Puisque dy/dx est la fonction dérivée d`une courbe, la dérivée d`une courbe peut être déterminée à tout moment. La valeur maximum/minimum peut donc être déterminée en fixant ces valeurs égales à 0, puis en déterminant les valeurs correspondantes. dy/dx = 0, 2ax+b = 0, x = -b/2a