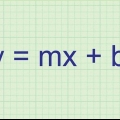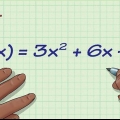La dérivée d`un exposant est l`exposant multiplié par la puissance -1 d`un nombre. Ainsi, la dérivée de x est 5x, et la dérivée de x est 3.5x. S`il y a déjà un nombre devant le x, multipliez-le par l`exposant. Par exemple : la dérivée de 3x est 12x. La dérivée de toute constante est nulle. Donc la dérivée de 8 est 0. La dérivée d`une somme est la somme de chaque dérivée. Par exemple : la dérivée de x + 3x est 3x + 6x. La dérivée d`un produit est le premier facteur multiplié par la dérivée du deuxième facteur plus le deuxième facteur multiplié par la dérivée du premier. Par exemple, la dérivée de x(2x + 1) est x(2) + (2x + 1)3x, ce qui est égal à 8x + 3x. La dérivée d`un quotient (disons, f/g) est [g(dérivé de f) - f(dérivé de g)]/g. Par exemple : la dérivée de (x + 2x - 21)/(x - 3) est (x - 6x + 15)/(x - 3). 






Détermination d'une dérivée
Teneur
Les dérivés peuvent être utilisés pour déterminer les caractéristiques utiles d`un graphique, telles que les maxima, les minima, les pics et les vallées et les pentes. Vous pouvez même les utiliser pour dessiner des équations complexes sans calculatrice graphique! Malheureusement, déterminer la dérivée d`une équation est souvent une tâche difficile, mais cet article vous aidera avec un certain nombre de trucs et astuces.
Pas

1. Comprendre la notation d`une dérivée. Les deux manières de notation suivantes sont les plus courantes, mais de nombreuses autres manières peuvent être trouvées sur Wikipédia.
- Notation de Leibniz Cette notation est le plus souvent utilisée lorsque l`équation contient y et x. Dy/dx signifie littéralement "la dérivée de y par rapport à x". Essayez de le considérer comme Δy/Δx pour les valeurs de x et y où la différence est infinitésimale. Cette explication donne naturellement la définition d`une limite par rapport à la dérivée : limh->0 (f(x+h)-f(x))/h. En appliquant cette notation à la dérivée seconde, écrivez : dy/dx.
- Notation de Lagrange La dérivée d`une fonction f s`écrit aussi f`(x). Cette notation se prononce comme "la fonction f de x". Cette notation est plus courte que celle de Leibniz et est utilisée lorsque l`on considère une dérivée comme une fonction. Pour les dérivés plus élevés, ajoutez simplement un autre " ` " prêt pour "F", faire ressembler la dérivée seconde à f``(x).

2. Comprendre ce qu`est un dérivé et à quoi il sert. Tout d`abord, pour trouver la pente d`un graphique linéaire, deux points sur la ligne sont pris et ces coordonnées sont insérées dans l`équation (y2 - oui1)/(X2 - X1). Mais cela n`est possible qu`avec des graphes linéaires. Pour les équations quadratiques et supérieures, le graphique est une courbe, donc la différence entre deux points n`est pas assez précise. Pour trouver la pente d`une tangente d`une parabole, deux points sont pris et remplis dans l`équation, pour déterminer la pente d`une ligne courbe : [f(x + dx) - f(x)]/dx. Dx signifie"delta x," quelle est la différence entre les deux coordonnées x des deux points du graphe. Notez que cette équation est la même que (y2 - oui1)/(X2 - X1), mais sous une forme différente. Comme on sait déjà que le résultat ne sera pas précis, une approximation indirecte est choisie. Pour trouver la pente de la tangente au point (x, f(x)), dx doit s`approcher de 0 pour que les deux points choisis soient presque les mêmes.Mais vous ne pouvez pas diviser par 0, donc après avoir rempli les valeurs des deux points, vous devez éliminer dedx dans le dénominateur. Si cela réussit, rendez dx égal à 0 et résolvez. C`est la pente de la tangente en (x, f(x)). La dérivée d`une équation est l`équation générale pour trouver la pente de n`importe quelle tangente d`un graphique. Cela peut sembler très difficile, mais les exemples ci-dessous vous montreront comment déterminer la dérivée.
Méthode 1 sur 4: Différenciation explicite

1. Utiliser une différenciation explicite si y est déjà d`un côté de l`équation.

2. Substituer une équation dans une autre équation [f(x + dx) - f(x)]/dx. Par exemple, l`équation y = x, dont la dérivée est [(x + dx) - x]/dx.

3. Développez dx davantage pour obtenir l`équation [dx(2x + dx)]/dx. Il est maintenant possible d`éliminer le dx dans le numérateur et le dénominateur. Le résultat est 2x + dx, et lorsque dx s`approche de 0, la dérivée devient 2x. C`est la pente de toute tangente au graphique y = x est 2x. Entrez simplement la valeur d`un point donné x dont vous voulez trouver la tangente dans l`équation.

4. Apprendre à reconnaître les régularités du même genre d`équations. Ci-dessous vous trouverez quelques.
Méthode 2 sur 4: Différenciation implicite

1. Utilisez la différenciation implicite lorsque votre équation ne peut pas être simplement écrite avec le y d`un côté du signe égal. Même si vous l`écrivez avec le y d`un côté, calculer dy/dx serait toujours une corvée. Voici un exemple de la façon de résoudre ce type d`équation.

2. Dans cet exemple, xy + 2y = 3x + 2y, remplacez jey par f(x), pour qu`il soit clair qu`il s`agit en fait d`une fonction. L`équation devient alors xf(x) + 2[f(x)] = 3x + 2f(x).

3. Pour trouver la dérivée de cette équation, différenciez (un mot impressionnant pour trouver la dérivée) vos deux côtés de l`équation par rapport à x. L`équation devient alors xf`(x) + 2xf(x) + 6[f(x)]f`(x) = 3 + 2f`(x).

4. Remplacez à nouveau f(x) par y. Attention à ne pas le faire avec f`(x) car c`est très différent de f(x).

5. Résoudre pour f`(x). La réponse de cet exemple est (3 - 2xy)/(x + 6y - 2).
Méthode 3 sur 4: Dérivés supérieurs

1. Prendre la dérivée supérieure d`une fonction signifie simplement prendre la dérivée de la dérivée. Par exemple, si la dérivée troisième est demandée, vous prenez la dérivée de la dérivée de la dérivée. Pour certaines équations, une dérivée supérieure devient égale à 0.
Méthode 4 sur 4: La règle de la chaîne

1. Si y est une fonction dérivable de z, et z est une fonction dérivable de x, alors y est une fonction composée de x, et la dérivée de y par rapport à x (dy/dx) est (dy/du)*(du /dx). La règle de la chaîne peut également être une équation composée, comme celle-ci : (2x - x). Pour trouver la dérivée de ceci; pensez simplement de la même manière que vous faites avec la gamme de produits. Multipliez l`équation par l`exposant et réduisez l`exposant par 1. Ensuite, multipliez l`équation par la dérivée qui tombe sous l`exposant (dans ce cas, 2x^4 - x). La réponse à ce problème devient alors 3(2x - x)(8x - 1).
Des astuces
- Chaque fois que vous voyez un problème apparemment insoluble, ne vous inquiétez pas. Essayez de diviser le problème en parties plus petites en appliquant les règles du produit, la règle du quotient, etc. Ensuite, différenciez les pièces individuelles.
- Pratiquez la règle du produit, la règle du quotient, la règle de la chaîne et, surtout, la différenciation implicite, car elles peuvent être assez délicates à partir du calcul.
- Connaissez votre calculatrice; essayez les différentes fonctions de votre calculatrice pour savoir comment elles fonctionnent. Il est certainement utile de savoir utiliser les fonctions tangente et dérivée, si votre calculatrice les possède.
- Mémorisez les dérivées trigonométriques les plus couramment utilisées et comment les utiliser.
Mises en garde
- N`oubliez pas que le signe moins est devant f(dérivé ou g) lorsque vous utilisez la règle du quotient ; il s`agit d`une erreur courante et entraînera une mauvaise réponse.
Articles sur le sujet "Détermination d'une dérivée"
Оцените, пожалуйста статью
Similaire
Populaire