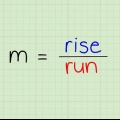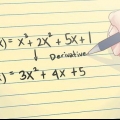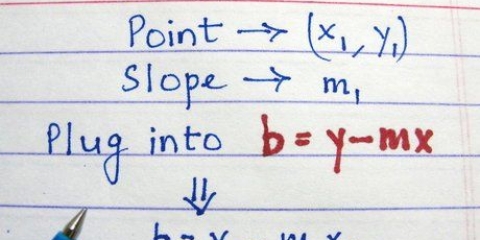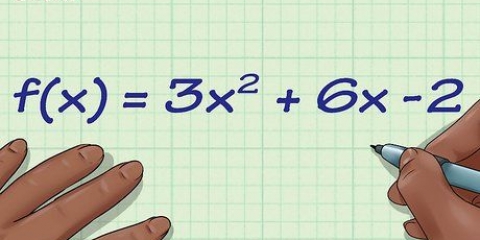Comment déterminer la pente d'une ligne

Teneur

La pente d`une ligne est une mesure de la vitesse à laquelle la ligne change. Cela peut être fait avec une ligne droite - où la pente vous indique exactement à quelle distance vers le haut (pente positive) ou vers le bas (pente négative) une ligne va sur une certaine distance. La pente peut également être utilisée pour une tangente à une courbe. Ou il pourrait s`agir d`une ligne courbe, utilisée en analyse, où la pente est également connue sous le nom de « dérivée » d`une fonction. Quoi qu`il en soit, pensez simplement à la pente comme au « taux de changement » d`un graphique : si la variable « x » augmente, à quel taux « y » change-t-il ?? C`est une façon de penser la pente comme cause et effet.

Pas

Méthode 1 sur 3: Trouver la pente d`une équation linéaire

Image intitulée Trouver la pente d`une équation Étape 1

1. Utilisez la pente pour déterminer à quel point et dans quelle direction (vers le haut ou vers le bas), une ligne va. Déterminer la pente d`une droite est facile, tant que vous avez ou pouvez établir une équation linéaire. Cette méthode ne fonctionne que lorsque :

Les variables n`ont pas d`exposant.
Il n`y a que deux variables, et aucune d`entre elles n`est des fractions (par exemple, ce qui suit ne peut pas être : $\frac{1}{X}$ ${frac{1}{x}}$ )
L`équation peut être simplifiée sous la forme $oui = m X + b$ $y=mx+b$ , par lequel m et b constantes (nombres tels que 3, 10, -12, $\frac{4}{3}, \frac{3}{5}$ ${frac{4}{3}},{frac{3}{5}}$ ).

2. Trouvez le nombre avant le x, généralement écrit "m" pour déterminer la pente. Si l`équation est déjà sous la forme correcte,

oui = m X + b

$y=mx+b$ , puis choisissez simplement le nombre dans la position `m` (mais s`il n`y a pas de nombre avant x alors la pente est 1). C`est donc aussi la pente! Sachez que ce numéro, m, est toujours multiplié par la variable, dans ce cas un `x`. Consultez les exemples suivants :

oui = 2 X + 6

$y=2x+6$

Pente = 2

oui = 2 - X

$y=2-x$

Pente = -1

oui = \frac{3}{8} X - dix

$y={frac{3}{8}}x-10$

pente = $\frac{3}{8}$ ${frac{3}{8}}$

Image intitulée Trouver la pente d`une équation Étape 3

3. Reconnaître l`équation où une variable est isolée si la pente n`est pas claire. Vous pouvez additionner, soustraire, multiplier, etc. pour isoler une variable (généralement le `y`). N`oubliez pas que quoi que vous fassiez d`un côté du signe égal (comme ajouter 3), vous devez également le faire de l`autre côté. Votre but ultime est une équation, comme

oui = m X + b

$y=mx+b$ . Par exemple:

Trouver la pente de $2 oui - 3 = 8 X + sept$ $2y-3=8x+7$

Convertissez-le sous la forme $oui = m X + b$ $y=mx+b$ :

2 oui - 3 + 3 = 8 X + sept + 3

$2a-3+3=8x+7+3$

2 oui = 8 X + dix

$2y=8x+10$

2 oui 2 = 8 X + dix 2

${frac{2y}{2}}={frac{8x+10}{2}}$

oui = 4 X + 5

$y=4x+5$

Déterminer la pente :

Pente = M = 4

Méthode 2 sur 3: Détermination de la pente avec deux points

Image intitulée Trouver la pente d`une équation Étape 4

1. Utilisez un graphique et deux points pour trouver rapidement la pente sans l`équation. Si vous avez un graphique et une ligne mais pas d`équation, vous pouvez toujours déterminer la pente facilement. Tout ce dont vous avez besoin, ce sont deux points sur la ligne, que vous appliquez à l`équation

oui 2 - {oui}_{1} X 2 - X_{1}

${frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Lors de la détermination de la pente, gardez à l`esprit les informations suivantes pour vous assurer que vous êtes sur la bonne voie :

Les pentes positives montent et vers la droite.
Les pentes négatives descendent et vers la droite.
Des pentes plus raides sont des lignes plus raides. Les pentes moins raides sont toujours plus progressives.
Les lignes horizontales parfaites ont une pente de zéro.
Les lignes parfaitement verticales n`ont aucune pente. Leur pente (ou pente) est « indéfinie ».

Image intitulée Trouver la pente d`une équation Étape 5

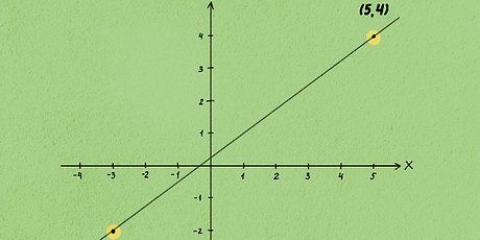
2. Choisissez deux points, en les mettant sous la forme simple (x, y). Utilisez le graphique (ou la question d`affectation) pour trouver les coordonnées x et y de deux points sur le graphique. Ils peuvent être constitués de deux points quelconques traversés par la ligne. Par exemple, supposons que dans cette méthode la droite passe par le point (2.4) et par (6.6).

Dans chaque paire, la coordonnée x est le premier nombre et la coordonnée y est le deuxième nombre après la virgule décimale.

Chaque coordonnée x sur une ligne a une coordonnée y correspondante.

Image intitulée Trouver la pente d`une équation Étape 6

3. Étiqueter les points x₁, oui₁, X₂, oui₂, et garde chaque point avec sa paire. En continuant avec notre premier exemple, en utilisant les points (2.4) et (6.6), étiquetez les coordonnées x et y de chaque point. Si tout s`est bien passé, vous vous retrouvez maintenant avec :

X₁: 2

oui₁: 4

X₂: 6

oui₂: 6

Image intitulée Trouver la pente d`une équation Étape 7

4. Remplacez ces points dans la `formule point-pente` pour trouver la pente. La formule suivante est utilisée pour déterminer la pente en utilisant deux points quelconques sur une ligne droite : $oui 2 - {oui}_{1} X 2 - X_{1}$ ${frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Remplacez simplement les quatre points et simplifiez :

Points d`origine : (2.4) et (6.6).

Appliquer à la formule point-pente :

6 - 4 6 - 2

${frac{6-4}{6-2}}$

Simplifiez pour la réponse finale :

$\frac{2}{4} = \frac{1}{2}$ ${frac{2}{4}}={frac{1}{2}}$ = pente

Image intitulée Trouver la pente d`une équation Étape 8

5. Comprendre le fonctionnement de la formule point-pente. La pente d`une ligne est indiquée par le changement de y à partir de x (y/x): combien la ligne monte divisé par combien la ligne continue vers la droite. L`augmentation de la ligne est la différence entre les valeurs y (rappelez-vous, l`axe des y monte et descend), et l`augmentation de la ligne est la différence entre les valeurs x (et l`axe des x va de de gauche à droite).

Image intitulée Trouver la pente d`une équation Étape 9

6. Apprenez d`autres façons que vous devez savoir pour déterminer la pente. L`équation de la pente est

oui 2 - {oui}_{1} X 2 - X_{1}

${frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Cela peut également être représenté par la lettre grecque `` (`delta`), signifiant `différence`. La pente peut également être représentée par Δy/Δx, ce qui signifie « différence de y » / « différence de x ». C`est exactement la même question que "Déterminer la pente entre…"

Méthode 3 sur 3: Utiliser le calcul différentiel pour trouver la pente d`une courbe

Image intitulée Trouver la pente d`une équation Étape 10

1. Examinez comment vous pouvez déterminer la dérivée de fonctions communes de différentes manières. Les dérivés vous donnent le taux de variation (ou pente) à un point sur une ligne. La ligne peut être courbe ou droite, peu importe. Rappelez-vous comment la ligne change à un moment donné, plutôt que comment la pente de la ligne entière change. La façon dont vous déterminez la dérivée dépend du type de fonction, alors examinez comment déterminer la dérivée des fonctions avant de continuer.

Lisez ici sur la détermination de la dérivée
Les dérivées les plus simples, celles des équations exponentielles standard, vous pouvez facilement trouver avec une méthode rapide. Vous l`utiliserez dans le reste de la méthode.

Image intitulée Trouver la pente d`une équation Étape 11

2. Comprendre quels problèmes vous obligent à calculer la pente à l`aide de dérivées. On ne vous demandera pas toujours explicitement la dérivée ou la pente d`une courbe. Vous pouvez également être interrogé sur le «taux de changement» au point (x, y). On peut vous demander une équation pour la pente du graphique, ce qui signifie simplement trouver la dérivée. Enfin, on peut vous demander « la pente de la ligne tangente en (x, y) ». Cela signifie encore une fois qu`il ne demande que la pente de la courbe à un point spécifique (x, y).

Avec cette méthode, posez-vous la question suivante : "Quelle est la pente de la droite

F (X) = 2 X 2 + 6 X

$f(x)=2x^{2}+6x$ au point (4.2)?"

La dérivée s`écrit souvent

F^{sexe} (X), {oui}^{sexe},

Image intitulée Trouver la pente d`une équation Étape 12

3.Trouver la dérivée de la fonction. Vous n`avez même pas besoin d`un vrai graphique, juste la fonction ou l`équation du graphique. Dans cet exemple, nous utilisons une fonction discutée précédemment,

4X+6 $F$

Image intitulée Trouver la pente d`une équation Étape 13

4.Substituer le point dans l`équation de la dérivée pour trouver la pente. Le différentiel d`une fonction vous donne la pente de la fonction en un point donné. En d`autres termes, f"(x) est la pente de la fonction à tout instant (x,f(x)). Donc pour ce problème d`exercice :