Trouver l'aire d'une pyramide : 12 étapes (avec photos)

Teneur

Pas
- Méthode 1 sur 2: Trouver l`aire d`une pyramide ordinaire
- Méthode 2 sur 2: Trouver l`aire d`une pyramide carrée
Nécessités

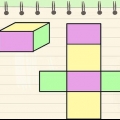
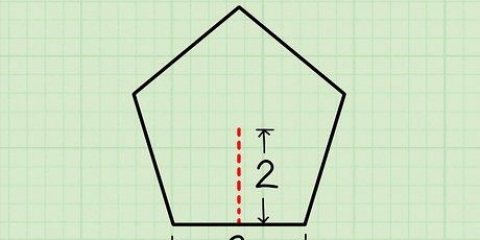
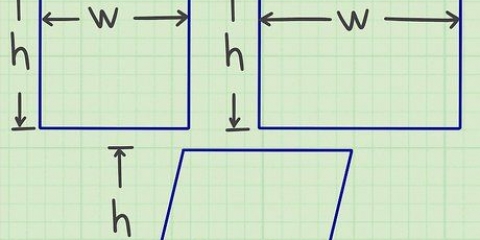
L`aire d`une pyramide peut être trouvée en ajoutant l`aire de sa base à l`aire de ses côtés. Lorsque vous travaillez avec des pyramides régulières, vous pouvez trouver l`aire à l`aide d`une formule tant que vous savez comment trouver l`aire de la base de la pyramide. Puisque la base peut être un polygone, il est utile de savoir déterminer l`aire de formes telles que les pentagones et les hexagones. Cependant, lorsque vous travaillez avec la pyramide carrée régulière, le calcul de la surface totale est facile, à condition de connaître la hauteur de l`inclinaison de la pyramide et la longueur de la base carrée.

Pas

Méthode 1 sur 2: Trouver l`aire d`une pyramide ordinaire

Image intitulée Trouver la surface d`une pyramide Étape 1

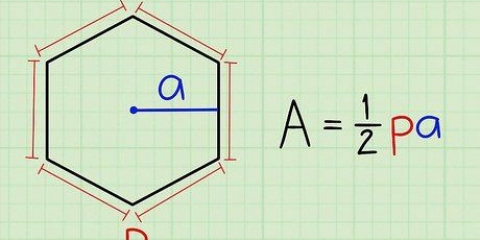
1. Écrivez la formule de l`aire d`une pyramide ordinaire. La formule est

s une = p \times h 2 + B

$SA={frac{pfois h}{2}}+B$ , par lequel

s une

$SA$ est égal à l`aire totale de la pyramide,

p

$p$ est égal au périmètre de la base,

h

$h$ est égal à la pente de la pyramide, et

B

$B$ est égal à l`aire de la base.

La formule de base pour l`aire d`une pyramide, régulière ou irrégulière, est Aire totale = Aire de base + Aire inclinée.
Ne pas confondre « hauteur d`inclinaison » avec « hauteur.La « hauteur d`inclinaison » est la distance diagonale entre le sommet de la pyramide et le bord de la base. La `hauteur` est la distance perpendiculaire du haut à la base.

Image intitulée Trouver la surface d`une pyramide Étape 2

2. Calculer le périmètre de la base. Si le périmètre n`est pas donné, mais est donné la longueur d`un bord de la base, vous pouvez calculer le périmètre en multipliant la longueur d`un bord par le nombre d`arêtes.

Par exemple, si vous voulez trouver l`aire d`une pyramide hexagonale, et que vous savez que la longueur d`un bord de la base est de 4 cm, vous calculez

4 \times 6 = 24

$4fois 6=24$ pour trouver le périmètre de la base, car un hexagone a six côtés. Donc le périmètre de la base est de 24 cm, donc la formule pour la zone ressemblera à ceci :

s une = 24 \times h 2 + B

$SA={frac{24fois h}{2}}+B$ .

Image intitulée Trouver la surface d`une pyramide Étape 3

3. Entrez la valeur de la hauteur de la pente dans la formule. Assurez-vous d`utiliser la hauteur inclinée, pas la hauteur perpendiculaire. La hauteur de pente doit être donnée dans le problème. Si vous ne connaissez pas la hauteur de la pente, vous ne pouvez pas utiliser cette méthode.

Supposons que la hauteur d`inclinaison d`une pyramide hexagonale soit de 12 cm, alors votre formule ressemblera à ceci :

s une = 24 \times 12 2 + B

$SA={frac{24fois 12}{2}}+B$ .

Image intitulée Trouver la surface d`une pyramide Étape 4

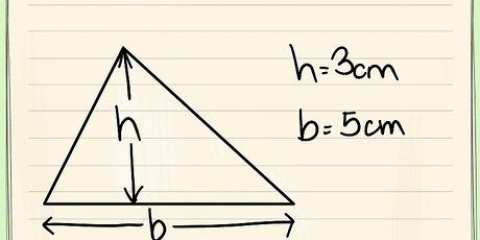
4. Calculer l`aire de la base. Comment faire cela dépend de la forme de la base. Pour cela, vous devez savoir comment déterminer les aires des polygones.

Par exemple, si vous avez affaire à une pyramide hexagonale, vous devez calculer l`aire de l`hexagone. La formule est

une = 3 \sqrt{3} \times s^{2} 2

$A={frac{3{sqrt{3}}times ^{{2}}}{2}}$ , par lequel

s

$s$ est la longueur d`un côté de l`hexagone. Étant donné que la longueur d`un côté de l`hexagone est de 4 cm, calculez comme suit :

une = 3 \sqrt{3} \times 4^{2} 2

$A={frac{3{sqrt{3}}fois 4^{{2}}}{2}}$

une = 3 \sqrt{3} \times 162

$A={frac{3{sqrt{3}}fois 16}{2}}$

une = 48 \sqrt{3} 2

$A={frac{48{sqrt{3}}}{2}}$

une = \frac{83.14}{2}

$A={frac{83.14}{2}}$

une = 41.57

$A=41,57$ .
Donc la superficie de la base est de 41,57 centimètres carrés.

Image intitulée Trouver la surface d`une pyramide Étape 5

5. Appliquer la zone de la base à la formule. Assurez-vous d`avoir la variable

B

$B$ remplace.

Supposons que l`aire de la base hexagonale soit de 41,57 cm. alors votre formule pour la zone ressemblerait à ceci:

s une = 24 \times 12 2 + 41.57

$SA={frac{24fois 12}{2}}+41,57$ .

Image intitulée Trouver la surface d`une pyramide Étape 6

6. Multiplier le périmètre de la base par la hauteur inclinée de la pyramide. Divisez le produit par deux. Cela vous donne la zone inclinée des faces de la pyramide.

Par exemple:

s une = 24 \times 12 2 + 41.57

$SA={frac{24fois 12}{2}}+41.57$

s une = \frac{288}{2} + 41.57

$SA={frac{288}{2}}+41.57$

s une = 144 + 41.57

$SA=144+41,57$

Image intitulée Trouver la surface d`une pyramide Étape 7

sept. Additionner les deux valeurs ensemble. La somme est la surface inclinée plus la surface de base, vous obtenez donc la surface totale de la pyramide en unités carrées.

Par exemple:

s une = 144 + 41, 57

$SA=144+41,57$

s une = 185, 57

$SA=185,57$
Ainsi, l`aire totale d`une pyramide hexagonale, avec une longueur de bord de base donnée de 4 cm et une hauteur de pente de 12 cm, est égale à 185,57 centimètres carrés.

Méthode 2 sur 2: Trouver l`aire d`une pyramide carrée

Image intitulée Trouver la surface d`une pyramide Étape 8

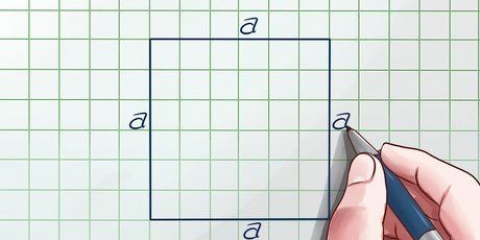
1. Ecrire la formule de l`aire d`une pyramide carrée. La formule est

s une = b 2 + 4 (b h 2)

$SA=b^{{2}}+4({frac{bh}{2}})$ , par lequel

b

$b$ est égal à la longueur d`un côté de la base, et

h

$h$ est égal à la pente de la pyramide.

Ne pas confondre « hauteur d`inclinaison » avec « hauteur.La « hauteur d`inclinaison » est la distance diagonale entre le sommet de la pyramide et le bord de la base. La `hauteur` est la distance perpendiculaire du haut à la base.
Notez que cette formule n`est qu`une autre façon de calculer la superficie totale = la superficie de base ( $b 2$ $b^{{2}}$ ) + Surface en pente ( $4 (b h 2)$ $4({frac{bh}{2}})$ ) écrire. Cette formule ne fonctionne que pour les pyramides carrées régulières.

Image intitulée Trouver la surface d`une pyramide Étape 9

2. Entrez les valeurs de la longueur des côtés et de la hauteur de la pente dans la formule. Assurez-vous de remplacer la longueur du côté de la base par

b

$b$ et la hauteur d`inclinaison de

h

$h$ .

Supposons que la longueur d`un côté de la base d`une pyramide carrée soit de 4 cm et que la hauteur de la pente soit de 12 cm, alors la formule ressemblerait à ceci :

s une = 4 2 + 4 ((4) (12) 2)

$SA=4^{{2}}+4({frac{(4)(12)}{2}})$ .

Image intitulée Trouver la surface d`une pyramide Étape 10

3. Carré la longueur d`un côté de la base. Cela vous donnera la superficie de la base.

Par exemple:

s une = 4 2 + 4 ((4) (12) 2)

$SA=4^{{2}}+4({frac{(4)(12)}{2}})$

s une = 16 + 4 ((4) (12) 2)

$SA=16+4({frac{(4)(12)}{2}})$

Image intitulée Trouver la surface d`une pyramide Étape 11

4. Multipliez la longueur d`un côté de la base par la hauteur de la pente et divisez par deux. puis multiplier par quatre. Cela vous donnera la surface inclinée de la pyramide.

Par exemple:

s une = 16 + 4 ((4) (12) 2)

$SA=16+4({frac{(4)(12)}{2}})$

s une = 16 + 4 (\frac{48}{2})

$SA=16+4({frac{48}{2}})$

s une = 16 + 4 (24)

$TN=16+4(24)$

s une = 16 + 96

$SA=16+96$

Image intitulée Trouver la surface d`une pyramide Étape 12

5. Ajouter la zone de la base à cette zone en pente. Cela vous donnera la superficie totale de la pyramide, en unités carrées.

Par exemple:

s une = 16 + 96

$SA=16+96$

s une = 112

$SA=112$
La surface totale d`une pyramide carrée, avec un côté de la base de 4 cm et une hauteur oblique de 12 cm, est donc de 112 centimètres carrés.