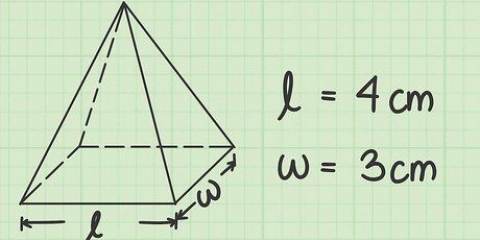Dans l`exemple, les côtés de la base de la pyramide font tous 5 cm, et vous calculez l`aire de la base comme suit : 
N`oubliez pas que les aires bidimensionnelles sont exprimées en carrés - centimètres carrés, mètres, kilomètres, etc. 
Dans l`exemple, nous supposons que la pyramide a une hauteur de 9 cm. Dans ce cas, multipliez l`aire de la base par cette valeur, comme suit : 
Rappelez-vous que les volumes sont exprimés en unités cubiques. Dans ce cas, comme toutes les mesures linéaires sont en centimètres, le volume est indiqué en centimètres cubes. 
Dans l`exemple, divisez 225 cm par 3 et la réponse est 75 cm pour le volume. 


Cette substitution ressemble à ceci : 


 .....(équation originale)
.....(équation originale) .....(carré des deux côtés)
.....(carré des deux côtés) .....(entrez des valeurs)
.....(entrez des valeurs) .....(fraction simplifiée)
.....(fraction simplifiée) .....(carré simplifié)
.....(carré simplifié) .....(soustraire)
.....(soustraire) .....(simplifier la racine)
.....(simplifier la racine)
Des calculs on déduit que la hauteur de la pyramide est de 12 cm. Utilisez-le avec les 10 cm de côté de la base pour calculer le volume de la pyramide : 









 ..........(équation ajustée)
..........(équation ajustée) ..........(remplacez h des deux côtés)
..........(remplacez h des deux côtés) ..........(soustrayez la racine carrée des deux côtés)
..........(soustrayez la racine carrée des deux côtés) ..........(remplir les nombres)
..........(remplir les nombres) ..........(simplifier les carrés)
..........(simplifier les carrés) ..........(soustraire les valeurs)
..........(soustraire les valeurs) ..........(simplifier la racine carrée)
..........(simplifier la racine carrée)Doublez cette valeur pour trouver la diagonale de la base carrée de la pyramide. Ainsi, la diagonale de la base de la pyramide est de 9,8 * 2 = 19,6 cm. 
Dans cet exemple de pyramide, la diagonale de la base est de 19,6 cm. Par conséquent, le côté est égal à : 





Calculer le volume d'une pyramide carrée
Teneur
Une pyramide carrée est une figure en trois dimensions avec une base carrée et des inclinaisons triangulaires qui se rencontrent en un point au-dessus de la base. Dans le cas où 


Pas
Méthode 1 sur 3: Déterminer le volume avec la surface de la base et la hauteur

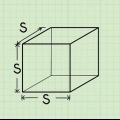
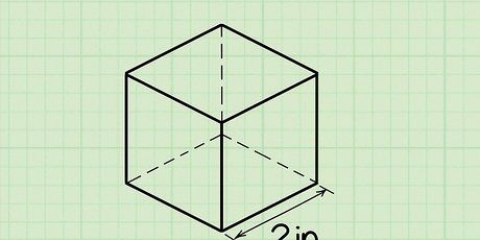
1. Mesurer la longueur du côté de la base. Puisque les pyramides carrées ont par définition une base carrée, tous les côtés de la base doivent avoir la même longueur. Donc avec une pyramide carrée il suffit de connaître la longueur d`un des côtés.
- Supposons que vous ayez une pyramide à base carrée dont les côtés ont une longueur de
. Vous utiliserez cette valeur pour calculer l`aire de la base.
- Si les côtés de la base ne sont pas de même longueur, alors vous avez un pyramide rectangulaire au lieu d`une pyramide carrée. La formule du volume d`une pyramide rectangulaire est très similaire à la formule des pyramides carrées. Dans le cas où
est la longueur de la base de la pyramide rectangulaire et
la largeur, puis le volume de la pyramide
.

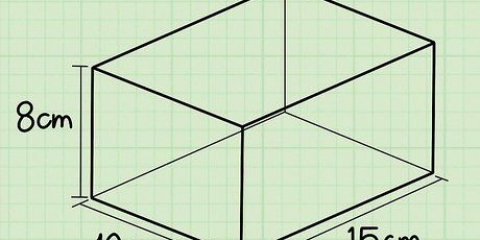
2. Calculer l`aire de la base. Pour déterminer le volume, vous avez d`abord besoin de la surface de la base. Pour ce faire, multipliez la longueur et la largeur de la base. Puisque la base d`une pyramide carrée est un carré, tous les côtés ont la même longueur, et l`aire de la base est égale au carré de la longueur de l`un de ses côtés (donc multiplié par lui-même).


3. Multiplier l`aire de la base par la hauteur de la pyramide. Ensuite, vous multipliez la surface de base par la hauteur de la pyramide. Pour rappel, la hauteur est la distance c`est la longueur du segment de droite du haut de la pyramide à la base, à angle droit.


4. Divisez cette réponse par 3. Enfin, vous déterminez le volume de la pyramide en divisant la valeur que vous venez de trouver (en multipliant l`aire de la base par la hauteur) par 3. Cela calcule le volume de la pyramide carrée.
Méthode 2 sur 3: Déterminer le volume avec l`apothème

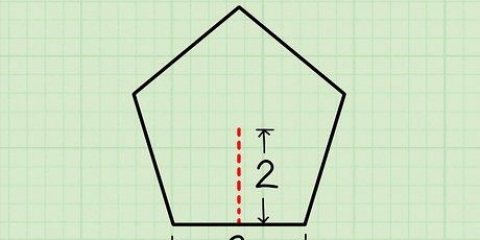
1. Mesurer l`apothème de la pyramide. Parfois la hauteur perpendiculaire de la pyramide n`est pas donnée (ou il faut la mesurer), mais l`apothème. Avec l`apothème, vous pouvez utiliser le théorème de Pythagore utiliser pour calculer la hauteur perpendiculaire.
- L`apothème d`une pyramide est la distance entre le sommet et le centre de l`un des côtés de sa base. Mesurez au centre d`un des côtés et non à l`un des coins de la base. Pour cet exemple, nous supposons que l`apothème est de 13 cm et la longueur d`un côté de la base est de 10 cm.
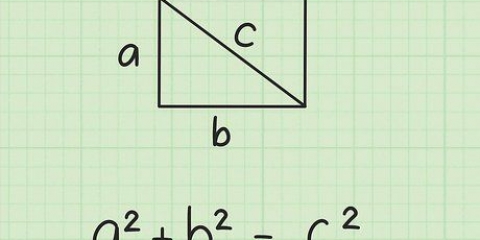
- Rappelez-vous que le théorème de Pythagore peut être exprimé comme l`équation
, par lequel
et
les jambes perpendiculaires sont du triangle rectangle et
l`hypoténuse.

2. Imaginez un triangle rectangle. Pour utiliser le théorème de Pythagore, vous avez besoin d`un triangle rectangle. Imaginez un triangle divisant la pyramide en deux et perpendiculaire à la base de la pyramide. L`apothème de la pyramide, appelé  , est l`hypoténuse de ce triangle rectangle. La base de ce triangle rectangle est la moitié de la longueur de
, est l`hypoténuse de ce triangle rectangle. La base de ce triangle rectangle est la moitié de la longueur de  , le côté de la base carrée de la pyramide.
, le côté de la base carrée de la pyramide.
 , est l`hypoténuse de ce triangle rectangle. La base de ce triangle rectangle est la moitié de la longueur de
, est l`hypoténuse de ce triangle rectangle. La base de ce triangle rectangle est la moitié de la longueur de  , le côté de la base carrée de la pyramide.
, le côté de la base carrée de la pyramide.
3. Affecter des variables aux valeurs. Le théorème de Pythagore utilise les variables a, b et c, mais il est utile de les remplacer par des variables significatives pour votre problème. l`apothème  prend la place de
prend la place de  dans le théorème de Pythagore. La jambe du triangle rectangle (
dans le théorème de Pythagore. La jambe du triangle rectangle ( ), prend la place de
), prend la place de  tu vas à la hauteur
tu vas à la hauteur  déterminer la pyramide, qui occupe la place de
déterminer la pyramide, qui occupe la place de  dans le théorème de Pythagore.
dans le théorème de Pythagore.
 prend la place de
prend la place de  dans le théorème de Pythagore. La jambe du triangle rectangle (
dans le théorème de Pythagore. La jambe du triangle rectangle ( ), prend la place de
), prend la place de  tu vas à la hauteur
tu vas à la hauteur  déterminer la pyramide, qui occupe la place de
déterminer la pyramide, qui occupe la place de  dans le théorème de Pythagore.
dans le théorème de Pythagore.


4. Utilisez le théorème de Pythagore pour calculer la hauteur perpendiculaire. Utiliser les valeurs mesurées  et
et  . Résolvez ensuite l`équation :
. Résolvez ensuite l`équation :
 et
et  . Résolvez ensuite l`équation :
. Résolvez ensuite l`équation : .....(équation originale)
.....(équation originale) .....(carré des deux côtés)
.....(carré des deux côtés) .....(entrez des valeurs)
.....(entrez des valeurs) .....(fraction simplifiée)
.....(fraction simplifiée) .....(carré simplifié)
.....(carré simplifié) .....(soustraire)
.....(soustraire) .....(simplifier la racine)
.....(simplifier la racine)
5. Utiliser la hauteur et la base pour calculer le volume. Après avoir appliqué ces calculs au théorème de Pythagore, vous avez maintenant les informations dont vous avez besoin pour calculer le volume de la pyramide. Utilisez la formule  et résolvez-les en vous assurant de donner la réponse en unités carrées.
et résolvez-les en vous assurant de donner la réponse en unités carrées.
 et résolvez-les en vous assurant de donner la réponse en unités carrées.
et résolvez-les en vous assurant de donner la réponse en unités carrées.



Méthode 3 sur 3: Détermination du volume avec la hauteur des jambes

1. Mesurer la hauteur des pattes de la pyramide. La hauteur des pattes est la longueur des bords de la pyramide, mesurée du haut à l`un des coins de la base. Comme ci-dessus, utilisez le théorème de Pythagore pour calculer la hauteur perpendiculaire de la pyramide.
- Dans cet exemple nous supposons que la hauteur des jambes est de 11 cm et que la hauteur perpendiculaire est de 5 cm.

2. Imaginez un triangle rectangle. Encore une fois, vous avez besoin d`un triangle rectangle pour pouvoir utiliser le théorème de Pythagore. Dans ce cas, cependant, la valeur inconnue est la base de la pyramide. Connue est la hauteur verticale et la hauteur des jambes. Imaginez maintenant couper la pyramide en diagonale d`un coin à l`autre, puis ouvrir la figure, le plan résultant ressemblerait à un triangle. La hauteur de ce triangle est la hauteur perpendiculaire de la pyramide. Cela divise le triangle exposé en deux triangles rectangles symétriques. L`hypoténuse de chacun des triangles rectangles est la hauteur des jambes de la pyramide. La base de chacun des triangles rectangles est la moitié de la diagonale de la base de la pyramide.

3. Attribuer des variables. Utilisez le triangle rectangle imaginaire et attribuez des valeurs au théorème de Pythagore. Vous connaissez la hauteur verticale,  qui est un côté du théorème de Pythagore,
qui est un côté du théorème de Pythagore,  . La hauteur des jambes de la pyramide,
. La hauteur des jambes de la pyramide,  forme l`hypoténuse de ce triangle rectangle imaginaire, et prend donc la place de
forme l`hypoténuse de ce triangle rectangle imaginaire, et prend donc la place de  . La diagonale inconnue de la base de la pyramide est le côté restant du triangle rectangle,
. La diagonale inconnue de la base de la pyramide est le côté restant du triangle rectangle,  Après avoir effectué ces substitutions, l`équation ressemble à ceci :
Après avoir effectué ces substitutions, l`équation ressemble à ceci :
 qui est un côté du théorème de Pythagore,
qui est un côté du théorème de Pythagore,  . La hauteur des jambes de la pyramide,
. La hauteur des jambes de la pyramide,  forme l`hypoténuse de ce triangle rectangle imaginaire, et prend donc la place de
forme l`hypoténuse de ce triangle rectangle imaginaire, et prend donc la place de  . La diagonale inconnue de la base de la pyramide est le côté restant du triangle rectangle,
. La diagonale inconnue de la base de la pyramide est le côté restant du triangle rectangle,  Après avoir effectué ces substitutions, l`équation ressemble à ceci :
Après avoir effectué ces substitutions, l`équation ressemble à ceci :


4. Calculer la diagonale de la base carrée. Vous devez réorganiser l`équation pour obtenir la variable  isoler, puis calculer sa valeur.
isoler, puis calculer sa valeur.
 isoler, puis calculer sa valeur.
isoler, puis calculer sa valeur. ..........(équation ajustée)
..........(équation ajustée) ..........(remplacez h des deux côtés)
..........(remplacez h des deux côtés) ..........(soustrayez la racine carrée des deux côtés)
..........(soustrayez la racine carrée des deux côtés) ..........(remplir les nombres)
..........(remplir les nombres) ..........(simplifier les carrés)
..........(simplifier les carrés) ..........(soustraire les valeurs)
..........(soustraire les valeurs) ..........(simplifier la racine carrée)
..........(simplifier la racine carrée)
5. Trouver le côté de la base de la diagonale. La base de la pyramide est un carré. La diagonale de chaque carré est égale à la longueur de l`un de ses côtés, multipliée par la racine carrée 2. Et donc vous pouvez trouver le côté d`un carré en divisant la diagonale par la racine carrée 2.


6. Calculer le volume en utilisant le côté et la hauteur. Revenez à la formule d`origine pour calculer le volume à l`aide de la hauteur latérale et perpendiculaire.




Des astuces
- Dans une pyramide carrée, la hauteur perpendiculaire, l`apothème et la longueur du bord de la base peuvent tous être calculés à l`aide du théorème de Pythagore.
Articles sur le sujet "Calculer le volume d'une pyramide carrée"
Оцените, пожалуйста статью
Similaire
Populaire