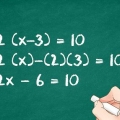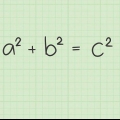Utiliser le théorème de Pythagore: 12 étapes (avec photos)

Teneur

Pas
- Méthode 1 sur 2: La longueur des côtés d`un triangle rectangle
- Méthode 2 sur 2: Calculer la distance entre deux points dans le plan
Des astuces

Le théorème de Pythagore décrit la longueur des côtés d`un triangle rectangle d`une manière si élégante et pratique qu`il est encore largement utilisé aujourd`hui. Cela indique que pour tout triangle rectangle, la somme des carrés des côtés droits est égale au carré de l`hypoténuse. En d`autres termes, pour un triangle rectangle (un triangle dont les côtés sont perpendiculaires entre eux), avec des côtés de longueur a et b et une hypoténuse de longueur c : a + b = c. Le théorème de Pythagore est l`un des piliers de la géométrie et a de nombreuses applications pratiques - par exemple, en utilisant ce théorème, il est très facile de trouver la distance entre deux points dans un plan plat.

Pas

Méthode 1 sur 2: La longueur des côtés d`un triangle rectangle

Image intitulée Utiliser le théorème de Pythagore Étape 1

1. Vérifiez si vous avez affaire à un triangle rectangle. Le théorème de Pythagore ne peut être utilisé que pour les triangles rectangles, donc avant de continuer, il est important d`établir que votre triangle répond à la définition d`un triangle rectangle. Heureusement, il n`y a qu`un seul facteur décisif ici - l`un des coins du triangle doit être un angle de 90 degrés.

Un indice est que les angles droits sont souvent marqués d`un petit crochet pour indiquer qu`il s`agit d`un angle de 90 degrés. Regarde s`il y a un tel support dans l`un des coins de ton triangle.

Image intitulée Utiliser le théorème de Pythagore Étape 2

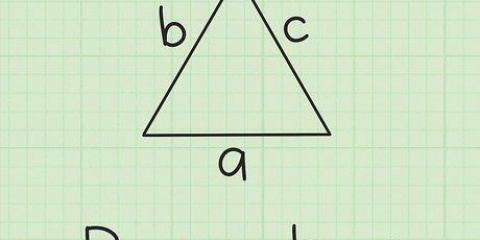
2. Attribuez les variables a, b et c aux côtés de votre triangle. Dans le théorème de Pythagore, les variables a et b font référence aux côtés droits de votre triangle et la variable c à l`hypoténuse - le côté long opposé à l`angle droit. Donc pour commencer vous affectez les variables a et b (l`ordre n`a pas d`importance) aux côtés droits et vous affectez c à l`hypoténuse.

Image intitulée Utiliser le théorème de Pythagore Étape 3

3. Déterminez quel côté du triangle vous voulez connaître. Le théorème de Pythagore permet de trouver la longueur de n`importe quel côté d`un triangle, à condition que deux des côtés soient connus. Déterminer lequel des côtés a une longueur inconnue--une, b, et/ouc. Si un seul est inconnu, vous pouvez passer à autre chose.

Supposons que l`on sache que l`hypoténuse a une longueur de 5 et que l`un des autres côtés a une longueur de 3. La longueur du côté restant est inconnue. Puisque deux des côtés sont connus, nous pouvons procéder au calcul de la longueur du côté inconnu! Nous reprendrons cet exemple plus tard.

Si la longueur de deux des côtés sont inconnus, alors vous devez déterminer la longueur d`au moins un côté supplémentaire pour pouvoir utiliser le théorème de Pythagore. Les fonctions trigonométriques de base peuvent vous y aider, à condition de connaître l`un des autres angles non droits du triangle.

Image intitulée Utiliser le théorème de Pythagore Étape 4

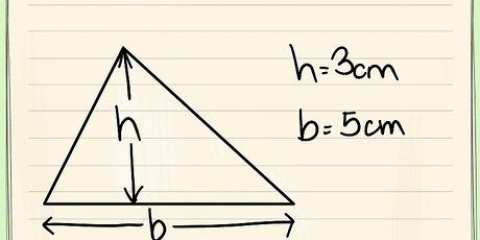
4. Calculer en utilisant l`équation et les connus. Insérez les valeurs des longueurs des côtés de votre triangle dans l`équation a + b = c. Rappelez-vous que a et b sont les côtés droits et c est l`hypoténuse.

Dans notre exemple nous connaissons la longueur d`un côté et celle de l`hypoténuse (3 & 5), nous écrivons donc notre équation comme ceci : 3² + b² = 5²

Image intitulée Utiliser le théorème de Pythagore Étape 5

5. Calculer les carrés. Pour résoudre votre équation, commencez par mettre au carré chacun des côtés connus. Si vous trouvez cela plus facile, vous pouvez laisser le pouvoir et le mettre au carré plus tard.

Dans notre exemple, nous cadrons 3 et 5 pour obtenir resp. 9 et 25 pour obtenir. Nous pouvons maintenant réécrire l`équation sous la forme 9 + b² = 25.

Image intitulée Utiliser le théorème de Pythagore Étape 6

6. Isoler la variable inconnue d`un côté du signe égal. En option, utilisez des opérations algébriques standard pour obtenir l`inconnu d`un côté du signe égal et les carrés de l`autre côté. Si vous essayez de trouver l`hypoténuse, alors c est déjà dans la position d`un côté, vous pouvez donc sauter cette étape.

Dans notre exemple, l`équation est maintenant 9 + b² = 25. à b² nous soustrayons 9 des deux côtés de l`équation. Cela nous laisse avec b² = 16.

Image intitulée Utiliser le théorème de Pythagore Étape 7

sept. Prendre la racine carrée des deux membres de l`équation. Vous devriez maintenant avoir un carré (variable) d`un côté de l`équation et un nombre de l`autre côté. Soustrayez maintenant la racine carrée des deux côtés pour trouver la longueur de l`inconnu.

Dans notre exemple, b² = 16, l`équation après avoir pris les racines carrées est b = 4. On peut donc dire que la longueur du côté inconnu de notre triangle est égale à 4.

Image intitulée Utiliser le théorème de Pythagore Étape 8

8. Utiliser le théorème de Pythagore en pratique. La raison pour laquelle le théorème de Pythagore est tellement utilisé est qu`il est applicable à la résolution de nombreux problèmes pratiques. Apprenez à reconnaître les triangles rectangles dans le monde qui vous entoure - partout où vous pouvez identifier un triangle rectangle avec un ou plusieurs objets, le théorème de Pythagore peut être utilisé pour trouver la longueur de l`un des côtés, à condition qu`il y ait deux côtés ou angles soyez célèbre.

Prenons un exemple du monde réel. Une échelle s`appuie contre un mur. Le bas de l`échelle est à 5 mètres du mur. L`échelle monte jusqu`à 20 mètres mesurés à partir du bas du mur. Quelle est la longueur de l`échelle?

"5 mètres est la distance au mur” et "l`échelle fait 20 mètres de haut". Cela donne une indication de la longueur des côtés du triangle. Puisque le mur et le sol sont censés former un angle droit et que l`échelle est diagonale au mur à un angle, on peut considérer cette disposition comme un triangle rectangle dont les côtés ont une longueur de a = 5 et b = 20. La longueur de l`échelle est l`hypoténuse, la variable inconnue c. Appliquons ici le théorème de Pythagore :

a² + b² = c²

(5)² + (20)² = c²

25 + 400 = c²

425 = c²

carré(425) = c

c = 20,6 . La longueur de l`échelle est (approximative) 20,6 mètres.

Méthode 2 sur 2: Calculer la distance entre deux points dans le plan

Image intitulée Utiliser le théorème de Pythagore Étape 9

1. Définir deux points dans le plan. Le théorème de Pythagore peut être utilisé très facilement pour déterminer la distance en ligne droite entre deux points du plan. Tout ce dont vous avez besoin sont les coordonnées x et y de deux points quelconques. Habituellement, ces coordonnées sont écrites comme (x, y).

Pour trouver la distance entre ces deux points, on considère chacun des points comme l`un des sommets d`un triangle rectangle, qui n`appartient pas à l`angle droit. Cela permet de trouver très facilement la longueur de a et b, après quoi c (l`hypoténuse et la distance entre les deux points) peut être calculé.

Image intitulée Utiliser le théorème de Pythagore Étape 10

2. Tracer les deux points sur un graphique. Dans un plan X-Y, pour chaque point (x, y), x est un point sur l`axe horizontal des x et y est un point sur l`axe vertical des y. Vous pouvez trouver la distance entre les deux sans les représenter graphiquement, mais cela vous donnera une référence visuelle pour vérifier si votre réponse a du sens.

Image intitulée Utiliser le théorème de Pythagore Étape 11

3. Trouvez la longueur des côtés droits de votre triangle. En considérant vos deux points comme les angles du triangle adjacent à l`hypoténuse, vous pouvez trouver les longueurs des côtés a et b. Vous pouvez le faire en utilisant le graphique ou en utilisant les formules |x₁ - X₂| pour le côté horizontal et |y₁ - oui₂| pour le côté vertical, où (x₁,oui₁) est le premier point et (x₂,oui₂) le deuxième point.

Supposons que nous ayons les points (6.1) et (3.5). La longueur du côté horizontal de notre triangle est :

|x₁ - X₂|

|3 - 6|

| -3 | = 3

La longueur du côté vertical est :

|y₁ - oui₂|

|1 - 5|

| -4 | = 4

On peut donc dire que la longueur des côtés de notre triangle rectangle est égale à a = 3 et b = 4.

Image intitulée Utiliser le théorème de Pythagore Étape 12

4. Utiliser le théorème de Pythagore pour trouver l`hypoténuse. La distance entre les deux points est la longueur de l`hypoténuse du triangle. Utilisez le théorème de Pythagore pour trouver l`hypoténuse du triangle, avec les côtés a, b et c.

Dans notre exemple, nous connaissons les points (3,5) et (6.1), et les longueurs des côtés sont a= 3 et b=4, nous déterminons donc l`hypoténuse comme suit :

(3)²+(4)²= c²

c= carré (9+16)

c= carré (25)

c= 5. La distance entre (3,5) et (6,1) est 5.

Des astuces

Si le triangle n`est pas un triangle rectangle, alors vous ne pouvez pas simplement utiliser le théorème de Pythagore.
L`hypoténuse est toujours :

la ligne opposée à l`angle droit
le côté le plus long du triangle rectangle
la variable c dans le théorème de Pythagore

sqrt(x) signifie "la racine carrée de x".

N`oubliez pas de toujours vérifier vos réponses. S`il semble qu`une réponse n`est pas correcte, vérifiez vos calculs ou recommencez.

Si vous ne connaissez qu`un côté du triangle, mais aussi l`un des autres angles (que l`angle droit), calculez d`abord un autre côté en utilisant ce que vous savez de la trigonométrie (sin, cos, tan) ou des proportions 30-60-90 / 45-45-90.

Une autre vérification - le côté le plus long s`oppose au plus grand angle et le côté le plus court s`oppose au plus petit angle.