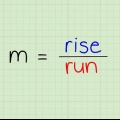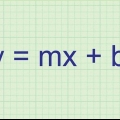Utiliser la formule de pente

Teneur

Pas
Des astuces

La formule de la pente est une façon courante d`écrire une équation linéaire. Cette formule s`écrit "y = mx + b" – où les lettres reçoivent une certaine valeur pour pouvoir résoudre cette équation, ou où l`équation est résolue pour trouver les valeurs des variables. Alors: "X" et "oui" sont les "X-" et "oui"-coordonnées d`une ligne, "m" est la pente (pente), le rapport (changement de y)/(changement de x), et "b" est l`intersection avec l`axe des y. Si vous voulez savoir comment utiliser la formule des pentes, vous êtes au bon endroit.

Pas

Méthode 1 sur 5: Utiliser la formule de la pente pour les problèmes

Image intitulée Utiliser le formulaire d`interception de pente (en algèbre) Étape 1

1. Lire le devoir. Avant de pouvoir continuer, vous devez lire attentivement le devoir afin de comprendre exactement ce qui vous est demandé. Lisez la déclaration suivante : Votre compte bancaire augmente linéairement chaque semaine. Si vous avez 560 $ sur votre compte bancaire après 20 semaines de travail et 585 $ après 21 semaines, comment exprimez-vous la relation entre le montant que vous avez gagné et le nombre de semaines que vous avez travaillées en utilisant la formule de la pente.

Image intitulée Utiliser le formulaire d`interception de pente (en algèbre) Étape 2

2. Pensez au problème en termes de formule de pente. Vous devriez l`écrire comme ceci : y = mx + b. La variable "m" est la pente et "b" est le point de départ où la ligne coupe l`axe des y. Notez que le problème indique que, " Votre compte bancaire augmente linéairement chaque semaine," ce qui signifie que vous économisez le même montant chaque semaine, ce qui signifie que vous avez une ligne droite et inclinée. Cette "constant," et un plan d`épargne continu est ce qui le rend linéaire. Si vous n`épargnez pas le même montant à chaque fois, ce n`est pas linéaire.

Image intitulée Utiliser le formulaire d`interception de pente (en algèbre) Étape 3

3. Trouver la pente de la droite. Pour trouver la pente, vous devez être en mesure de déterminer le taux de changement. Si vous commencez avec 560€ et que la semaine suivante vous avez 585€, alors vous avez gagné 25€ après 1 semaine de travail. Vous pouvez également le calculer en soustrayant 560 € à 585 €. 585-560 = 25.

4. Trouver l`intersection avec l`axe des y. Pour trouver cette intersection, également appelée "b" en y = mx + b, vous devez connaître le point de départ de votre problème (c`est-à-dire l`intersection avec l`axe des y). Cela signifie que vous devez savoir avec combien d`argent vous avez commencé. Si vous aviez 560 $ après 20 semaines de travail et que vous savez que vous avez gagné 25 $ en une semaine, utilisez la multiplication suivante pour calculer combien vous avez gagné en 20 semaines. 20 x 25 = 500, vous avez donc gagné 500 $ au cours de ces semaines.

Parce qu`après 20 semaines vous avez 560 € et avez également gagné 500 €. alors vous savez combien vous avez commencé en soustrayant 500 de 560. 560 - 500 = 60.

Alors le "b" ou le point de départ, est de 60.

5. Écrire l`équation. Maintenant que vous connaissez la pente, m vaut 25 (gagner 25 dollars par semaine) et le point de départ b est 60, vous pouvez intégrer ceci dans l`équation :

y = mx + b

y = 25x + 60

6. Tester si l`équation est correcte. le "oui" est le montant d`argent que vous avez gagné et le "X" le nombre de semaines que vous avez travaillé. Voyez combien d`argent vous avez gagné en un nombre donné de semaines en entrant ces données dans l`équation. Essayez deux exemples :

Combien d`argent as-tu gagné en 10 semaines? remplir "dix" dans pour le "X" à découvrir ici.

y = 25x + 60 =

y = 25(10) + 60 =

y = 250 + 60 =

y = 310. Après 10 semaines, vous avez gagné 310 €.

Combien de semaines faut-il travailler pour gagner 800 euros? remplir "800" dans pour le "oui"-variable de l`équation pour obtenir derrière la valeur de "X" venir.

y = 25x + 60 =

800 = 25x + 60 =

800 - 60 =

25x = 740 =

25x/25 = 740/25 =

x = 29.6. Vous pouvez gagner 800 euros en 30 semaines environ.

Méthode 2 sur 5: Conversion d`une équation en formule de pente

1. Écrire l`équation. Supposons que vous avez affaire à l`équation suivante, 4 ans +3x = 16.

2. Isoler le terme y d`un côté de l`équation. Pour ce faire, soustrayez 3x des deux côtés de l`équation. L`équation devrait maintenant ressembler à ceci : 4y = -3x +16.

4 ans + 3x = 16

4 ans + 3x - 3x = 16 -3x

4y = -3x +16

3. Divisez tous les termes par le coefficient de y. C`est le nombre de la variable y. Ne mettez pas de chiffre ici, alors vous avez terminé. S`il y a un nombre (le coefficient), divisez chaque terme de l`équation par ce nombre. Dans ce cas, le coefficient y est de 4, vous devez donc diviser 4x, -3x et 16 par 4 pour obtenir la réponse finale. Voici comment cela fonctionne :

4y = -3x +16 =

/₄oui = /₄X +/_{4 = (par division)}

y = /₄X + 4 (en simplifiant la division)

4. Déterminer les termes de l`équation. Lorsque vous utilisez l`équation pour tracer une ligne, rappelez-vous que "oui" la coordonnée y est en "-3/4" la pente ou la pente, "X" est alors l`abscisse et "4" l`intersection avec l`axe des y.

Méthode 3 sur 5: La formule de pente utilisant un point et la pente

1. Écrire l`équation de la droite comme formule de la pente. Écrivez d`abord y = mx + b. Vous pouvez ensuite remplir l`équation une fois que vous avez suffisamment de données. Supposons que vous vouliez résoudre le problème suivant : Trouver l`équation d`une droite de pente 4 passant par le point (-1, -6).

2. Remplissez les détails. Tu le sais "m" est égal à la pente de la droite, est égal à 4 et que "oui" et "X" respectivement le "X" et "oui" les coordonnées sont. Dans ce cas, les données sont "X" = -1 et "oui" = -6. "b" représente l`intersection avec l`axe des y ; cette valeur n`est pas encore connue. Voici à quoi ressemble l`équation maintenant :

y = -6, m = 4, x = -1 (les valeurs données)

y = mx + b (la formule)

-6 = (4)(-1) + b (après avoir rempli)

3. Résoudre pour "b". Il s`agit maintenant de travailler à "b," trouver l`intersection avec l`axe des y. Multipliez 4 et -1 puis soustrayez le résultat de -6. Voici comment procéder :

-6 = (4)(-1) + b

-6 = -4 + b

-6 - (-4) = -4 -(-4) + b

-6 - (-4) = b (terme droit simplifié)

-2 = b (terme à gauche simplifié)

4. Écrire l`équation. Maintenant, c`est à votre tour "b," vous pouvez remplir les valeurs nécessaires dans la formule de pente. Il suffit de connaître la pente et l`intersection avec l`axe des y (b) :

m = 4, b = -2

y = mx + b

y = 4x -2 (substitution)

Méthode 4 sur 5: Écrire la formule de la pente à l`aide de deux points

1. Notez les deux points. Avant de pouvoir faire l`équation de la ligne, vous écrivez d`abord les deux points qui sont donnés. Supposons que vous vouliez résoudre le problème suivant : Trouvez l`équation de la droite passant par les points (-2, 4) et (1, 2).

2. Utilisez ces points pour trouver la pente de l`équation. La formule pour déterminer la pente de la droite passant par deux points est (y₂ - oui₁) / (X₂ - X₁). Vous avez affaire aux coordonnées (x₁, Oui₁) = (-2, 4) et (x₂, Oui₂ ) = (1, 2). Insérez maintenant cette valeur dans l`équation et résolvez pour m.

(oui₂ - oui₁) / (X₂ - X₁) =

(2 - 4)/(1 - -2) =

-2/3 = m

La pente de la droite est -2/3.

3. Choisissez l`un des points à résoudre pour l`intersection avec l`axe des y. Peu importe la paire que vous choisissez. Choisissez celui avec lequel vous travaillez le plus facilement Supposons que vous choisissiez le point (1, 2). Maintenant, remplissez ceci dans l`équation "y = mx + b". Résoudre pour "b":

y = 2, x, = 1, m = -2/3

y = mx + b

2 = (-2/3)(1) + b

2 = -2/3 + b

2 - (-2/3) = b

2 + 2/3 = b, ou b = /₃

4. Remplir les nombres dans l`équation d`origine. Maintenant que vous savez que la pente est égale à 2/3 et l`intersection avec l`axe des y ("b") est égal à 2 2/3, vous pouvez insérer ces valeurs dans l`équation d`origine de la ligne et vous avez terminé.

y = mx + b

y = /₃X + 2 2/3

Méthode 5 sur 5: Tracer la ligne

1. Écris l`équation et utilise-la pour tracer la ligne. Supposons que vous ayez l`équation suivante : y = 4x + 3.

2. Commencer par l`intersection avec l`axe des y. L`intersection avec l`axe des y est donnée par "+3" ou "b" dans l`équation. C`est le point (0, 3). Indiquez ce point avec un point.

3. Utilisez la pente de la ligne pour trouver les coordonnées de l`autre point. Parce que vous savez que la pente est représentée par "m=4," pouvez-vous dire que la pente est égale à y/x=4/1. Cela signifie que chaque fois que la ligne monte de 4 points sur l`axe des y, elle se décale d`un point vers la droite sur l`axe des x. Donc, vous commencez au point (0, 3) et montez 4 points et 1 point vers la droite, pour finir au point (1, 7) comme point suivant de la ligne.

Si la pente est négative, la droite descend de gauche à droite.

4. Reliez les deux points avec une ligne. Utilisez un crayon et une règle pour cela. C`est tout ce que vous devez faire et vous avez tracé une ligne parfaite selon l`équation donnée. Deux points suffisent pour tracer la ligne. Si nécessaire, vérifiez en dessinant quelques points supplémentaires.

Des astuces

Un exemple de diminution et d`augmentation linéaires est le changement constant de la vitesse d`un objet, mesurée en mètres par seconde, distance mesurée au fil du temps.
L`algèbre est active. Vous n`avez pas seulement à lire et à comprendre la théorie, vous devez également travailler avec pour comprendre comment elle fonctionne.
C`est la vraie façon de vous montrer : le changement de y par rapport au changement de x s`appelle l`augmentation (croissance) ou la diminution (décroissance) de la différence de y divisée par la différence de x. Diviser par est aussi appelé un rapport, une fraction ou un rapport. Voici le rapport "le degré de changement.
Au début, travaillez également les exercices simples sur papier. Si vous travaillez sur des exercices plus difficiles par la suite, vous bénéficierez beaucoup de cette méthode car elle vous donne une meilleure idée de la marche à suivre pour faire un graphique.
Rappelez-vous : la multiplication vient avant l`addition, donc y = mx + b ; donc d`abord m ×x puis x+b.
Ne vous contentez pas de lire les exemples. Écrivez-les et pratiquez les différentes étapes afin de bien comprendre l`ensemble du processus.
Vous impressionnerez certainement votre professeur si vous apprenez à comprendre comment appliquer une équation linéaire à toutes sortes de problèmes.
Le système de coordonnées cartésiennes utilisé en algèbre pour faire un graphique, etc. est nommé d`après son inventeur français, l`utilisant pour les coordonnées sur les cartes. Des systèmes similaires sont utilisés dans divers domaines des mathématiques, ainsi que dans l`astronomie, la navigation, les écrans d`ordinateur, les enseignes au néon et les tableaux de bord, ou pour localiser presque tout.
La pente d`une ligne mesure le rapport du changement vertical (y) par rapport au changement horizontal (x). Il peut s`agir de points sur une ligne, mais aussi d`un certain taux de croissance linéaire ou de la pente d`une colline.