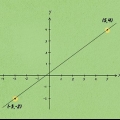
L`axe des x est l`axe horizontal ; l`axe des y est l`axe vertical. Les coordonnées d`un point s`écrivent  .
. Par exemple, un segment de ligne peut avoir une extrémité à  et un autre sur
et un autre sur  .
. 
Par exemple, avec les points  et
et  , votre formule ressemblera à ceci:
, votre formule ressemblera à ceci: 


Par exemple:



Par exemple:



Puisque vous déterminez la racine carrée, vous devrez peut-être arrondir votre réponse. Puisque vous travaillez à partir d`un système de coordonnées, votre réponse sera en général "unités" et non en centimètres, mètres ou toute autre unité. Par exemple:

 unités.
unités.
Calcul de la longueur d'une ligne à l'aide de la formule de distance
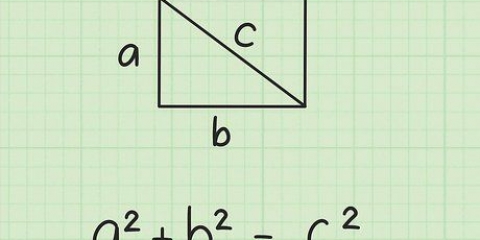
Vous pouvez mesurer la longueur d`une ligne verticale ou horizontale dans un système de coordonnées en ajoutant simplement les coordonnées ; cependant, mesurer la longueur d`une ligne diagonale est un peu plus délicat. Vous pouvez utiliser la formule de distance pour déterminer la longueur d`une telle ligne. Cette formule est en fait le théorème de Pythagore, qui devient clair lorsque vous imaginez le segment de droite comme l`hypoténuse d`un triangle rectangle. En utilisant une formule géométrique simple, mesurer des lignes le long d`un certain nombre de coordonnées devient une tâche relativement simple.
Pas
Partie 1 sur 2: Écriture de la formule

1. Écrivez la formule de distance. La formule dit que  , par lequel
, par lequel  est égal à la distance de la ligne,
est égal à la distance de la ligne,  est égal aux coordonnées du premier point d`extrémité du segment de ligne, et
est égal aux coordonnées du premier point d`extrémité du segment de ligne, et  est égal aux coordonnées du deuxième point d`extrémité du segment de ligne.
est égal aux coordonnées du deuxième point d`extrémité du segment de ligne.
 , par lequel
, par lequel  est égal à la distance de la ligne,
est égal à la distance de la ligne,  est égal aux coordonnées du premier point d`extrémité du segment de ligne, et
est égal aux coordonnées du premier point d`extrémité du segment de ligne, et  est égal aux coordonnées du deuxième point d`extrémité du segment de ligne.
est égal aux coordonnées du deuxième point d`extrémité du segment de ligne.
2. Déterminer les coordonnées des extrémités du segment de ligne. Ceux-ci ont peut-être déjà été donnés. Sinon, comptez le long de l`axe des x et de l`axe des y pour trouver les coordonnées.
 .
. et un autre sur
et un autre sur  .
.
3. Appliquer les coordonnées à la formule de distance. Assurez-vous d`entrer les valeurs pour les variables correctes. Les deux  -les coordonnées sont à l`intérieur des premières parenthèses, et les deux
-les coordonnées sont à l`intérieur des premières parenthèses, et les deux  -les coordonnées sont à l`intérieur des deux crochets suivants.
-les coordonnées sont à l`intérieur des deux crochets suivants.
 -les coordonnées sont à l`intérieur des premières parenthèses, et les deux
-les coordonnées sont à l`intérieur des premières parenthèses, et les deux  -les coordonnées sont à l`intérieur des deux crochets suivants.
-les coordonnées sont à l`intérieur des deux crochets suivants. et
et  , votre formule ressemblera à ceci:
, votre formule ressemblera à ceci: 
Partie 2 sur 2: Calcul de la distance

1. Calculer la somme négative entre parenthèses. Selon l`ordre des opérations, chaque calcul entre parenthèses doit être calculé en premier.
- Par exemple:

2. Placer la valeur entre parenthèses. L`ordre des opérations indique qu`il faut ensuite calculer les puissances.



3. Additionner les nombres sous le signe radical. Vous pouvez faire ce calcul comme si vous travailliez avec des nombres entiers.



4. Résoudre pour ré  . Pour approximer la réponse finale, trouvez la racine carrée de la somme sous le radical.
. Pour approximer la réponse finale, trouvez la racine carrée de la somme sous le radical.
 . Pour approximer la réponse finale, trouvez la racine carrée de la somme sous le radical.
. Pour approximer la réponse finale, trouvez la racine carrée de la somme sous le radical.
 unités.
unités.Des astuces
- Ne confondez pas cette formule avec d`autres, telles que la formule du milieu, la formule de la pente ou l`équation d`une ligne.
- Gardez à l`esprit l`ordre des opérations lors du calcul de la réponse. Soustraire d`abord, puis carré la différence, puis additionner et calculer la racine carrée.
Articles sur le sujet "Calcul de la longueur d'une ligne à l'aide de la formule de distance"
Оцените, пожалуйста статью
Populaire