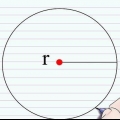
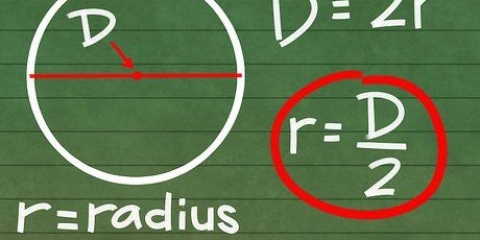
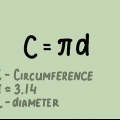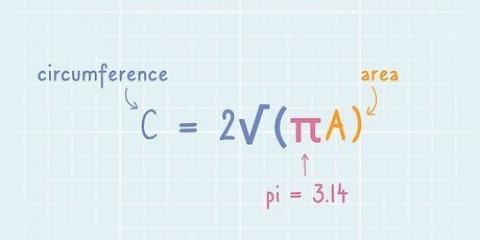Le rayon (r) d`un cercle est la distance d`un point du cercle au centre du cercle. Le diamètre (ré) d`un cercle est la distance d`un point du cercle à un autre point directement opposé au cercle, passant par le centre du cercle. La lettre grecque pi (π) représente le rapport de la circonférence divisée par le diamètre et est représentée par le nombre 3.14159265..., un nombre irrationnel qui n`a ni chiffre final ni motif reconnaissable de chiffres répétés. Ce nombre est souvent arrondi à 3,14 pour les calculs standards. 
Dans la plupart des problèmes mathématiques, le rayon ou le diamètre est donné. 
Par exemple : Quelle est la circonférence d`un cercle de 3 cm de rayon? Écrivez la formule : C = 2πr Remplissez les variables : C = 2π3 Multiplier : C = (2*3*π) = 6π = 18,84 cm Par exemple : Quelle est la circonférence d`un cercle d`un diamètre de 9 m? Écrivez la formule : C = d Remplissez les variables : C = 9π Multiplier : C = (9*π) = 28,26 m 
Déterminer la circonférence d`un cercle d`un diamètre de 5 m. C = d = 5π = 15,7 m Déterminer la circonférence d`un cercle de 10 m de rayon. C = 2πr = C = 2π10 = 2 *10 *π = 62,8 m. 

Le rayon (r) d`un cercle est la distance d`un point du cercle au centre du cercle. Le diamètre (ré) d`un cercle est la distance d`un point du cercle à un autre point directement opposé au cercle, passant par le centre du cercle. La lettre grecque pi (π) représente le rapport de la circonférence divisée par le diamètre et est représentée par le nombre 3.14159265..., un nombre irrationnel qui n`a ni chiffre final ni motif reconnaissable de chiffres répétés. Ce nombre est généralement arrondi à 3,14 pour les calculs de base. 
Dans la plupart des problèmes mathématiques, le rayon ou le diamètre est donné. 
Par exemple : quelle est l`aire d`un cercle de 3 m de rayon? Écris la formule : A = r. Remplissez les variables : A = 3. Carré du rayon : r = 3 = 9 Multiplier par pi : une = 9π = 28,26 m Par exemple : quelle est l`aire d`un cercle d`un diamètre de 4 m? Écrire la formule : A = (d/2). Remplissez les variables : A = (4/2). Divisez le diamètre par 2: j/2 = 4/2 = 2 Carré du résultat : 2 = 4 Multiplier par pi : une = 4π = 12,56 m 
Trouver l`aire d`un cercle de 7 m de diamètre. A = (d/2) = (7/2) = π(3,5) = 12,25 * π= 38,47 m. Trouver l`aire d`un cercle de 3 m de rayon. A = r = π * 3 = 9 * = 28,26 m 

Par exemple : calculez la circonférence d`un cercle de rayon (x + 1). Écrivez la formule : C = 2πr Remplissez les informations données : C = 2π(x+1) 
Par exemple : calculez la circonférence d`un cercle de rayon (x = 1). C = 2πr = 2π(x+1) = 2πx + 2π1 = 2πx +2π = 6,28x + 6,28 Si la valeur de « x » est donnée plus tard dans le problème, vous pouvez le brancher et obtenir un nombre entier. 
Trouver l`aire d`un cercle de rayon 2x. A = r = (2x) = π4x = 12,56x Trouver l`aire d`un cercle de diamètre (x+2). A = (d/2) = π((x +2)/2) = ((x +2)/4)π
Calcul de la circonférence et de l'aire d'un cercle
Teneur
La circonférence (C) d`un cercle est sa circonférence, ou la distance qui l`entoure. L`aire (A) d`un cercle est l`espace occupé par le cercle ou l`aire délimitée par le cercle. L`aire et la circonférence peuvent être calculées avec des formules simples à partir du rayon ou du diamètre du cercle et de la valeur de pi.
Pas
Partie 1 sur 3: Calcul de la circonférence

1. Apprendre la formule de la circonférence d`un cercle. Deux formules peuvent être utilisées pour calculer la circonférence d`un cercle : C = 2πr ou C = d, où est la constante mathématique et approximativement égale à 3,14,r est égal au rayon et ré égal au diamètre.
- Puisque le rayon d`un cercle est égal à deux fois son diamètre, ces équations sont essentiellement les mêmes.
- Les unités de circonférence peuvent être n`importe quelle unité de mesure de longueur : kilomètres, mètres, centimètres, etc.

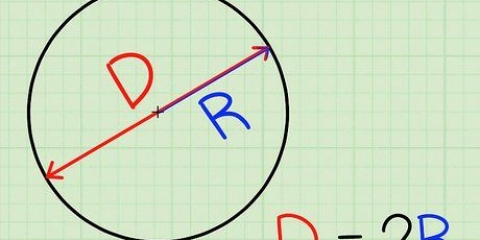
2. Comprendre les différentes parties de la formule. Il y a trois éléments pour trouver la circonférence d`un cercle : rayon, diamètre et. Le rayon et le diamètre sont liés : le rayon est égal à la moitié du diamètre, tandis que le diamètre est égal à deux fois le rayon.

3. Mesurer le rayon ou le diamètre du cercle. Placez une règle sur un bord du cercle, en passant par le centre et de l`autre côté du cercle. La distance du centre du cercle est le rayon, tandis que la distance de l`autre extrémité du cercle est le diamètre.

4. Traiter et résoudre les variables. Une fois que vous avez déterminé le rayon et/ou le diamètre du cercle, vous pouvez mettre ces variables dans l`équation appropriée. Si vous avez le faisceau, utilisez C = 2πr, mais si vous connaissez le diamètre alors utilisez C = d.

5. Entraînez-vous avec quelques exemples. Maintenant que vous avez appris la formule, il est temps de pratiquer avec quelques exemples. Plus vous résolvez de problèmes, plus il sera facile de les résoudre à l`avenir.
Partie 2 sur 3: Calcul de la surface

1. Apprendre la formule de l`aire d`un cercle. L`aire d`un cercle peut être calculée soit à l`aide de son diamètre, soit de son rayon, avec deux formules différentes : A = r ou A = (d/2), où est la constante mathématique approximativement égale à 3,14,r le rayon et ré le diamètre.
- Puisque le rayon d`un cercle est égal à la moitié de son diamètre, ces équations sont essentiellement les mêmes.
- Les unités de surface peuvent être n`importe quelle unité de longueur au carré : km carré (km), mètres carrés (m), centimètres carrés (cm), etc.

2. Comprendre les différentes parties de la formule. Il y a trois éléments pour trouver la circonférence d`un cercle : rayon, diamètre et. Le rayon et le diamètre sont liés l`un à l`autre : le rayon est égal à la moitié du diamètre, tandis que le diamètre est égal au double du rayon.

3. Mesurer le rayon ou le diamètre du cercle. Placez une extrémité d`une règle à un point du cercle, en passant par le centre et de l`autre côté du cercle. La distance du centre du cercle est le rayon, tandis que la distance de l`autre point du cercle est le diamètre.

4. Remplissez les variables et résolvez-les. Une fois que vous avez déterminé le rayon et/ou le diamètre du cercle, vous pouvez brancher ces variables dans l`équation appropriée. Si vous connaissez le rayon, utilisez A = r, mais si vous connaissez le diamètre alors utilisez A = (d/2).

5. Entraînez-vous avec quelques exemples. Maintenant que vous avez appris la formule, il est temps de pratiquer avec quelques exemples. Plus vous résolvez de problèmes, plus il sera facile de résoudre d`autres problèmes.
Partie 3 sur 3: Calcul de la superficie et du périmètre avec des variables

1. Déterminer le rayon ou le diamètre du cercle. Certains problèmes donnent un rayon ou un diamètre avec une variable, comme r = (x + 7) ou d = (x + 3). Dans ce cas, vous pouvez toujours déterminer la zone ou le périmètre, mais votre réponse finale contiendra également cette variable. Notez le rayon ou le diamètre comme indiqué dans la déclaration.
- Par exemple : calculez la circonférence d`un cercle de rayon (x = 1).

2. Écrivez la formule avec les informations données. Que vous souhaitiez calculer la superficie ou le périmètre, vous suivez toujours les étapes de base pour remplir ce que vous savez. Écrivez la formule pour l`aire ou le périmètre, puis remplissez les variables données.

3. Résoudre le problème comme si la variable était un nombre. À ce stade, vous pouvez simplement résoudre le problème comme vous le feriez normalement, en traitant la variable comme s`il s`agissait simplement d`un autre nombre. Vous aurez peut-être besoin du utiliser la propriété distributive pour simplifier la réponse finale.

4. Entraînez-vous avec quelques exemples. Maintenant que vous avez appris la formule, il est temps de pratiquer avec quelques exemples. Plus vous résolvez de problèmes, plus il devient facile d`en résoudre de nouveaux.
Articles sur le sujet "Calcul de la circonférence et de l'aire d'un cercle"
Оцените, пожалуйста статью
Similaire
Populaire