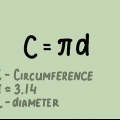Comment calculer le rayon d'un cercle

Teneur

Le rayon d`un cercle est la distance entre le centre du cercle et le bord. Le diamètre d`un cercle est la longueur de la ligne droite qui peut être tracée entre deux points de la sphère ou du cercle et passant par son centre.On vous demande souvent de calculer le rayon d`un cercle à partir d`autres données. Dans cet article, vous apprendrez à calculer le rayon d`un cercle en fonction d`un diamètre, d`une circonférence et d`une aire donnés. La quatrième méthode est une méthode plus avancée pour déterminer le centre et le rayon d`un cercle en fonction des coordonnées de trois points sur le cercle.

Pas

Méthode 1 sur 3: Calculez le rayon si vous connaissez le diamètre

Image intitulée Calculer le rayon d`un cercle Étape 1

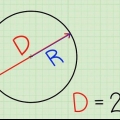
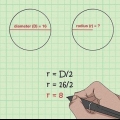
1. Rappelez-vous quel est le diamètre. Le diamètre d`un cercle est la longueur de la ligne droite qui peut être tracée entre deux points de la sphère ou du cercle et passant par son centre. Le diamètre est la ligne la plus longue qui peut être tracée à travers un cercle et divise le cercle en deux moitiés. La longueur du diamètre est également égale à la longueur de deux fois le rayon. La formule du diamètre est la suivante : D= 2r, où "ré" signifie diamètre et "r" pour poutre. La formule du rayon peut être dérivée de la formule précédente et est donc : r = D/2.

Image intitulée Calculer le rayon d`un cercle Étape 2

2. Divisez le diamètre par 2 pour trouver le rayon. Si vous connaissez le diamètre d`un cercle, il vous suffit de le diviser par 2 pour trouver le rayon.

Par exemple, si le diamètre d`un cercle est 4, alors la droite est 4/2, ou 2.

Méthode 2 sur 3: Calculez le rayon si vous connaissez la circonférence

Image intitulée Calculer le rayon d`un cercle Étape 3

1. Vous souvenez-vous de la formule de la circonférence d`un cercle ?. La circonférence d`un cercle est la distance autour du cercle. Une autre façon de voir les choses est la suivante : le périmètre est la longueur de la ligne que vous obtenez si vous coupez le cercle ouvert en un point et posez la ligne droite. La formule pour la circonférence d`un cercle est O = 2πr, où "r" est le rayon et est la constante pi, soit 3,14159... La formule du rayon est alors r = O/2π.

Habituellement, vous pouvez arrondir pi à deux chiffres après la virgule (3,14), mais vérifiez d`abord avec votre professeur.

Image intitulée Calculer le rayon d`un cercle Étape 4

2. Calculer le rayon avec la circonférence donnée. Pour calculer le rayon en fonction de la circonférence, divisez la circonférence par 2π, soit 6,28

Par exemple, si la circonférence est de 15, alors le rayon est r = 15/2π, soit 2,39.

Méthode 3 sur 3: Calculez le rayon si vous connaissez les coordonnées de trois points sur le cercle

Image intitulée Calculer le rayon d`un cercle Étape 9

1. Comprendre que trois points peuvent définir un cercle. Trois points quelconques sur une grille définissent un cercle tangent aux trois points. C`est le cercle circonscrit du triangle formant les points. Le centre du cercle peut tomber à l`intérieur ou à l`extérieur du triangle, selon la position des trois points, et en même temps c`est le "intersection" du triangle.Il est possible de calculer le rayon du cercle si vous connaissez les coordonnées xy des trois points en question.

A titre d`exemple, prenons trois points définis comme suit : P1 = (3,4), P2 = (6, 8) et P3 = (-1, 2).

Image intitulée Calculer le rayon d`un cercle Étape 10

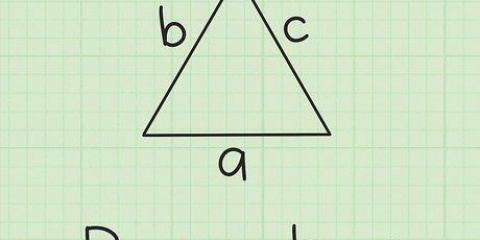
2. Utilisez la formule de distance pour calculer les longueurs des trois côtés du triangle, que nous appelons a, b et c. La formule de la distance entre deux coordonnées (x₁, oui₁) et (x₂, oui₂) est la suivante : distance = (( x₂ - X₁) + (y₂ - oui₁)). Traitez maintenant les coordonnées des trois points dans cette formule pour trouver les longueurs des trois côtés du triangle.

Image intitulée Calculer le rayon d`un cercle Étape 11

3. Calculer la longueur du premier côté a, qui va du point P1 à P2. Dans notre exemple, les coordonnées de P1 (3.4) et de P2 (6.8), donc la longueur du côté a = ((6 - 3) + (8 - 4)).

a = (3 + 4)

a = (9 + 16)

a = 25

a = 5

Image intitulée Calculer le rayon d`un cercle Étape 12

4. Répétez le processus pour trouver la longueur du deuxième côté b, qui va de P2 à P3. Dans notre exemple, les coordonnées de P2 (6.8) et de P3 sont (-1.2), donc la longueur du côté b = ((-1 - 6) + (2 - 8)).

b= (-7 + -6)

b = (49 + 36)

b = √85

b = 9.23

Image intitulée Calculer le rayon d`un cercle Étape 13

5. Répétez le processus pour trouver la longueur du troisième côté c, qui va de P3 à P1. Dans notre exemple, les coordonnées de P3 (-1,2) et de P1 (3,4), donc la longueur du côté c =√((3 - -1) + (4 - 2)).

c= (4 + 2)

c = (16 + 4)

c = 20

c = 4.47

Image intitulée Calculer le rayon d`un cercle Étape 14

6. Utilisez ces longueurs dans la formule de recherche de rayon : (abc)/(√(a + b + c)(b + c - a)(c + a - b)(a + b - c)).. Le résultat est le rayon de notre cercle!

Les longueurs du triangle sont les suivantes : a = 5, b = 9.23 et c = 4.47. Donc la formule pour le rayon ressemble à ceci : r = (5 * 9.23*4.47)/(√(5 + 4.47 + 9.23)(4.47 + 9.23 - 5)(9.23 + 5 - 4.47)(5 + 4.47 – 9.23)).