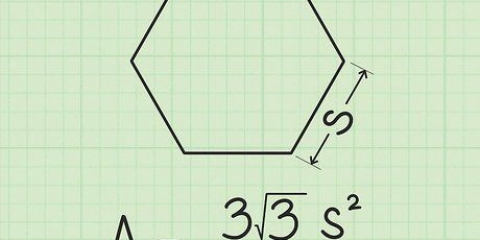
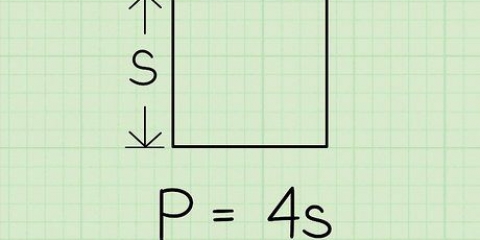
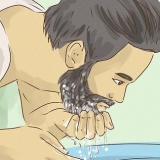
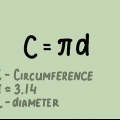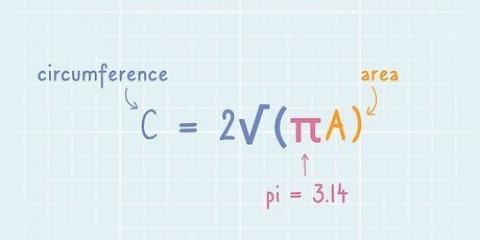Passez un fil autour de la circonférence, aussi précisément que possible. Marquez le fil lorsque le cercle est terminé, puis mesurez la longueur du fil avec une règle. 




=3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11 *12) - 4/(12*13*14) ... Vous appliquez cette formule en prenant d`abord 2 puis en ajoutant et en soustrayant alternativement des fractions, avec le numérateur 4 et le dénominateur le produit de 3 entiers consécutifs qui augmentent à chaque nouvelle itération. Chaque fraction consécutive commence par une série d`entiers où le premier nombre de la série est le dernier nombre de la série précédente (dans la fraction précédente). Même si vous ne le faites que quelques fois, vous vous rapprocherez bientôt de pi. 


pi=2 *(Arcsin(sqrt(1 - x^2))) + abs(Arcsin(x)). Arcsin fait référence à un sinus inverse en radians Sqrt est l`abréviation de la racine carrée de Abs est l`abréviation de valeur absolue x^2 est une certaine puissance, dans ce cas x au carré.
Calculer pi
Teneur
Pi (π) est l`un des nombres les plus importants et les plus fascinants en mathématiques. Simplement affiché comme 3.14, est utilisé comme constante pour calculer la circonférence d`un cercle, en utilisant son rayon ou son diamètre. C`est aussi un nombre irrationnel, ce qui signifie que vous pouvez le calculer avec un nombre infini de décimales sans jamais rencontrer de motif répétitif. Cela rend difficile, mais pas impossible, de travailler avec précision.
Pas
Méthode 1 sur 5: Calculer Pi à l`aide d`un cercle

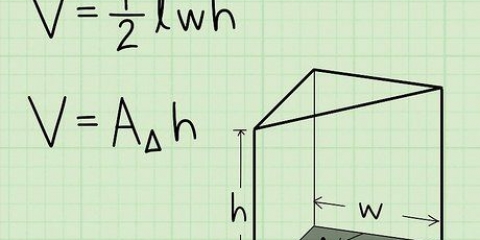
1. Assurez-vous d`utiliser un cercle parfait. Cette méthode ne fonctionnera pas avec une ellipse, une ellipse ou autre chose qu`un vrai cercle. Un cercle est défini comme tous les points d`un plan équidistants d`un point central donné. Par exemple, les couvercles d`un pot de confiture sont un bel outil à utiliser pour cet exercice. Vous pouvez calculer approximativement une valeur de Pi avec ceci. Même le crayon le plus fin et le plus pointu est encore énorme par rapport à la précision requise pour un calcul exact du nombre Pi.

2. Mesurez la circonférence du cercle aussi précisément que possible. La circonférence est la longueur de toute la circonférence du cercle. Étant donné que cela tourne en rond, cela peut être un peu difficile à mesurer (c`est pourquoi Pi est si important).

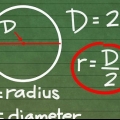
3. Mesurer le diamètre du cercle. Le diamètre est la longueur de la section transversale d`un cercle passant par le centre du cercle.

4. Utilisez la formule. La circonférence d`un cercle peut être trouvée avec la formule C=π*d=2*π*r. Donc pi est égal à la circonférence du cercle divisé par le diamètre. Entrez vos nombres dans une calculatrice : le résultat devrait être d`environ 3.devrait avoir 14 ans.

5. Pour un résultat plus précis, répétez ce processus pour plusieurs cercles, puis faites la moyenne des résultats. Vos lectures peuvent ne pas être parfaites lorsqu`il s`agit d`une lecture individuelle, mais avec le temps, la moyenne devrait être une très bonne approximation de Pi.
Méthode 2 sur 5: Calcul de Pi à l`aide de séries infinies

1. Profitez de la série Grégory-Leibniz. Les mathématiciens ont trouvé plusieurs séquences mathématiques qui, si elles sont suivies à l`infini, peuvent calculer Pi à un nombre énorme de décimales. Certaines de ces séquences sont si complexes qu`il faut des superordinateurs pour les traiter. L`une des plus simples, cependant, est la série Gregory-Leibniz. Peut-être pas très efficace, mais il produit un nombre plus précis pour pi à chaque itération, se terminant finalement à 5 décimales après 500.000 itérations. Voici la formule à utiliser.
- =(4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15) ...
- Prenez 4 et soustrayez 4 divisé par 3 de ceci. Puis ajouter 4 divisé par 5. Puis soustraire 4 divisé par 7 à nouveau. Continuez à répéter ce modèle avec un numérateur 4 et un nombre impair consécutif au dénominateur. Plus vous faites cela, plus vous vous rapprochez de pi.

2. Profitez des gammes Nilakantha. Ceci est une autre série infinie qui vous permet de calculer pi et n`est pas difficile à comprendre. Bien qu`un peu plus compliqué, vous pouvez calculer pi beaucoup plus rapidement avec qu`avec la formule de Leibniz.
Méthode 3 sur 5: Calcul de Pi à l`aide du problème de l`aiguille de Buffon

1. Essayez l`expérience suivante pour calculer pi en lançant des hot-dogs. Pi figure également dans l`expérience de pensée appelée Problème de l`aiguille de Buffon, qui essaie de déterminer la probabilité que des objets de forme similaire, lancés au hasard, atterrissent entre ou sur une série de lignes parallèles sur le sol. Il s`avère que si la distance entre les lignes est égale à la longueur des objets lancés, alors le nombre de fois où les objets atterrissent sur une ligne après plusieurs lancers peut être utilisé pour calculer pi.
- Les scientifiques et les mathématiciens n`ont pas encore découvert un moyen de calculer exactement pi, car ils n`ont pas encore trouvé de matériau si fin que vous puissiez effectuer des calculs exacts avec.
Méthode 4 sur 5: Calcul de Pi avec une limite

1. Choisissez un grand nombre. Plus le nombre est grand, plus votre calcul sera précis.

2. Utilisez le nombre, que nous appellerons x, dans cette formule pour calculer pi :x *péché (180 / x). Pour que cela fonctionne, assurez-vous que votre calculatrice est réglée sur degrés. La raison pour laquelle cela s`appelle une limite est que son résultat est "limité" à pi. Au fur et à mesure que vous augmentez votre nombre x, le résultat se rapproche de plus en plus de la valeur de pi.
Méthode 5 sur 5: Arcsinus et fonction sinus inverse
1. Choisissez un nombre entre -1 et 1. C`est parce que l`arc sinus n`est pas défini pour les nombres supérieurs à 1 ou inférieurs à -1.
2. Utilisez le nombre dans la formule suivante et le résultat est à peu près égal à pi.
Des astuces
- Calculer pi est amusant et stimulant, mais si vous calculez trop de décimales, cela ne sera pas très utile .Les astronomes disent qu`il ne faut pas plus de 39 décimales pour que le nombre pi fasse des calculs très précis.
Articles sur le sujet "Calculer pi"
Оцените, пожалуйста статью
Populaire