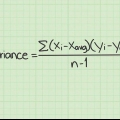Si la mesure expérimentale est de 60 cm, le calcul de l`imprécision devra également être arrondi à un nombre entier. Par exemple, l`imprécision de cette mesure peut être de 60 cm ± 2 cm, mais pas de 60 cm ± 2.2 cm. Si votre lecture expérimentale est égale à 3.4 cm, alors l`imprécision devra également être arrondie à 0,1 cm. Par exemple, l`imprécision de cette mesure peut être de 3.4 cm ± .être 1 cm, mais pas 3.4cm ± 1cm. 
Regardez attentivement le bord de la balle et la règle pour avoir une idée de la fiabilité de votre mesure. Dans une règle standard, les marques de 0,5 cm sont clairement marquées - mais supposons que vous puissiez vous rapprocher un peu plus que cela. S`il semble que vous puissiez obtenir à moins de 0,3 cm avec votre mesure, alors l`imprécision est de 0,3 cm. Maintenant, nous allons mesurer le diamètre de la balle. Supposons que vous obtenez 7,6 cm comme réponse. Notez maintenant la mesure estimée avec l`inexactitude. Le diamètre de la boule est de 7,6 cm ± 0,3 cm. 
Supposons que vous ne puissiez pas vous approcher beaucoup plus de 0,2 cm avec une règle ordinaire. Donc, l`imprécision est de ± 0,2 cm. Supposons que vous mesuriez que la pile de boîtes ensemble mesure 22 cm. Il ne vous reste plus qu`à diviser cette valeur de mesure et l`imprécision par 10 (le nombre de cases). 22 cm/10 = 2,2 cm et 0,2 cm/10 = 0,02 cm. Cela signifie que l`épaisseur de 1 boîte est égale à 2,20 cm ± 0,02 cm. 



0,43 s – 0,42 s = 0,01 s 0,52s - 0,42s = 0,1s 0,35 s - 0,42 s = -0,07 s 0,29 s - 0,42 s = -0,13 s 0,49 s - 0,42 s = 0,07 s Additionnez maintenant les carrés des différences : (0,01 s) + (0,1 s) + (-0,07 s) + (-0,13 s) + (0,07 s)= 0,037 s. Trouvez la moyenne de ces carrés additionnés en divisant le résultat par 5. 0,037 s/5 = 0,0074 s. 



(10 cm ± .4 cm) - (3 cm ± .2cm) = (10cm - 3cm) ± (.4 cm +. 2cm) = 7 cm ± 0,6 cm (6 cm ± 0,2 cm) = (0,2 / 6) x 100 et ajoutez-y un signe %. C`est 3,3%
Ainsi:
(6 cm ± 0,2 cm) x (4 cm ± 0,3 cm) = (6 cm ± 3,3%) x (4 cm ± 7,5%) (6 cm x 4 cm) ± (3.3 + 7,5) = 24 cm ± 10,8 % = 24 cm ± 2,6 cm (10 cm ± 0,6 cm) (5 cm ± 0,2 cm) = (10 cm ± 6 %) ÷ (5 cm ± 4 %) (10 cm 5 cm) ± (6% + 4%) = 2 cm ± 10 % = 2 cm ± 0,2 cm 
(2,0 cm ± 1.0 cm) = (2,0 cm) ± (1,0 cm) x 3 = 8,0 cm ± 3 cm
Calculer l'inexactitude
Teneur
Lorsque vous prenez une mesure tout en collectant des données, vous pouvez supposer qu`il y a un "valeur réelle" est dans la plage des mesures que vous avez faites. Si vous souhaitez calculer l`imprécision de vos lectures, vous devrez trouver la meilleure estimation de votre lecture et en tenir compte lors de la soustraction ou de l`ajout de l`imprécision de la lecture.
Pas
Méthode 1 sur 3: Apprendre les bases

1. Déterminer la forme correcte pour l`inexactitude. Supposons que vous mesuriez la longueur d`un bâton d`environ 4,2 cm, avec une marge de 1 millimètre. Cela signifie que le bâton mesure presque certainement 4,2 cm, mais peut être légèrement plus grand ou plus petit que cette longueur, avec une marge d`erreur de 1 millimètre.
- Notez ceci comme suit : 4,2 cm ± 0,1 cm. Vous pouvez réécrire ceci comme : 4,2 cm ± 1 mm, car 0,1 cm = 1 mm.

2. Arrondissez la lecture expérimentale au même nombre de décimales que l`imprécision. Les mesures impliquant des inexactitudes sont généralement arrondies à 1 ou 2 chiffres significatifs. Le point clé est que vous arrondissez les mesures de l`expérience au même nombre de décimales que l`imprécision, pour garder les mesures cohérentes.

3. Calculer l`imprécision d`une seule mesure. Supposons que vous mesuriez le diamètre d`une boule ronde avec une règle. C`est délicat car il est difficile de déterminer exactement où se trouve le bord extérieur de la balle et comment le mesurer avec la règle. Supposons que la règle puisse trouver le diamètre avec une précision de 0,1 cm - cela ne signifie pas que vous pouvez mesurer le diamètre de la balle à ce niveau de précision.

4. Calculer l`imprécision d`une seule mesure de plusieurs objets. Supposons que vous mesuriez la hauteur d`une pile de 10 boîtiers de CD qui ont tous des dimensions. Supposons que vous vouliez savoir quelle est l`épaisseur d`une boîte. Cette lecture est si petite que le pourcentage d`inexactitude sera élevé. Mais si vous mesurez 10 cases, vous pouvez diviser le résultat et diviser simplement son imprécision par le nombre de cases dans la pile pour trouver l`épaisseur de 1 case.

5. Effectuez cette mesure plusieurs fois. Pour augmenter la précision de votre mesure, que vous mesuriez la longueur d`un objet ou le temps qu`il a fallu pour parcourir une certaine distance, vous augmenterez les chances d`une mesure précise si vous prenez plusieurs mesures. La détermination de la moyenne de toutes les mesures se traduira finalement par une meilleure détermination de l`inexactitude d`une mesure.
Méthode 2 sur 3: Calcul de l`inexactitude de plusieurs mesures

1. Prendre plusieurs mesures. Supposons que vous vouliez calculer combien de temps il faut pour qu`une balle tombe de la table sur le tour. Pour de meilleurs résultats, vous devrez effectuer la même mesure au moins plusieurs fois - disons que nous le faisons cinq fois. Ensuite, vous devrez calculer la moyenne de ces 5 mesures, puis ajouter ou soustraire l`écart type de celle-ci, pour le meilleur résultat.
- Supposons que vous ayez les lectures suivantes : 0,43 s, 0,52 s, 0,35 s, 0,29 s et 0,49 s.

2. Déterminer la moyenne des mesures. Vous faites cela en additionnant les cinq ensemble et en divisant la somme par 5, le nombre de valeurs mesurées. 0,43 s + 0,52 s + 0,35 s + 0,29 s + 0,49 s = 2.08 s. Partager maintenant 2.08 par 5. 2.05/08 = 0,42 s. La moyenne est de 0,42 s.

3. Déterminer la variance de ces mesures. Pour ce faire, déterminez la différence entre chacune des 5 mesures et la moyenne. Soustraire les lectures de 0,42 s. Voici les 5 différences :

4. Déterminer l`écart type. Ceci peut être trouvé en calculant la racine carrée de la variance. Le carré de 0,0074 s = 0,09 s, donc l`écart type est de 0,09 s.

5. Donner la valeur finale mesurée. Pour ce faire, notez la moyenne des valeurs mesurées ainsi que l`écart type ajouté et soustrait. Étant donné que la moyenne des lectures est de 0,42 s et l`écart type est de 0,09 s, la lecture finale est de 0,42 s ± 0,09 s.
Méthode 3 sur 3: Opérations arithmétiques avec imprécision

1. Ajout d`imprécision. Vous faites cela en additionnant les lectures et en ajoutant leurs inexactitudes :
- (5 cm ± .2 cm) + (3 cm ± .1cm) =
- (5cm + 3cm) ± (.2 cm +. 1cm) =
- 8cm ± .3 cm

2. Soustraire l`inexactitude. Pour ce faire, soustrayez les valeurs mesurées et ajoutez les inexactitudes :
3. Multiplier l`inexactitude.
Pour multiplier l`imprécision, multipliez les mesures et ajoutez l`imprécision RELATIVE (en pourcentage) :
Le calcul des inexactitudes par multiplication ne fonctionne pas avec des valeurs absolues (comme pour l`addition et la soustraction), mais avec des valeurs relatives. Vous obtenez l`imprécision relative en divisant l`imprécision absolue par la valeur mesurée, puis en la multipliant par 100.
Par exemple:
Pour multiplier l`imprécision, multipliez les mesures et ajoutez l`imprécision RELATIVE (en pourcentage) :
Le calcul des inexactitudes par multiplication ne fonctionne pas avec des valeurs absolues (comme pour l`addition et la soustraction), mais avec des valeurs relatives. Vous obtenez l`imprécision relative en divisant l`imprécision absolue par la valeur mesurée, puis en la multipliant par 100.
Par exemple:
Ainsi:
4. Partage de l`inexactitude.
Pour diviser l`imprécision, divisez les mesures et ajoutez l`imprécision RELATIVE :
Cette procédure équivaut à une multiplication!
Pour diviser l`imprécision, divisez les mesures et ajoutez l`imprécision RELATIVE :
Cette procédure équivaut à une multiplication!

5. Augmenter de façon exponentielle une lecture inexacte. Pour augmenter de façon exponentielle une mesure inexacte, augmentez la mesure d`une certaine puissance, puis multipliez l`imprécision par cette puissance :
Des astuces
- Vous pouvez afficher les résultats et l`inexactitude par défaut dans leur ensemble, ou pour chaque résultat dans un ensemble de données. Une règle générale est que les données obtenues à partir de plusieurs mesures sont moins précises que celles obtenues directement à partir d`une mesure individuelle.
Mises en garde
- L`imprécision décrite ici ne s`applique qu`aux cas où des statistiques normales (gaussiennes, en forme de cloche) sont utilisées. D`autres spreads nécessitent une méthode différente pour décrire l`inexactitude.
- Une bonne recherche ne s`arrête jamais "les faits" ou quoi "vrai" est. Bien qu`une mesure soit très susceptible de se situer dans une certaine plage d`imprécision, il n`y a aucune garantie qu`elle. Il est inhérent aux valeurs mesurées scientifiques qu`il existe une possibilité que les valeurs mesurées soient incorrectes.
Articles sur le sujet "Calculer l'inexactitude"
Оцените, пожалуйста статью
Populaire