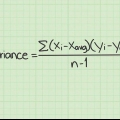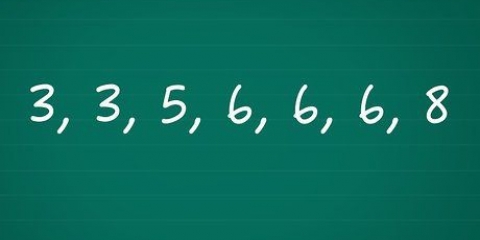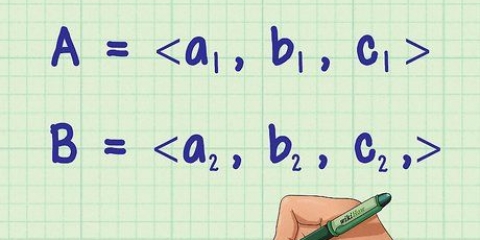Si vous avez deux (ou plus) points de données avec la même valeur dans une colonne, prenez la moyenne des positions que ces points de données auraient normalement et donnez aux points de données cette moyenne comme nouvelle position.
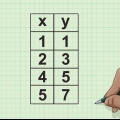
Dans l`exemple de droite, il y a deux cinq qui seraient normalement en position 2 et 3. C`est deux les mêmes chansons, donc prendre la moyenne de leurs positions. La moyenne de 2 et 3 est de 2,5, donc donnez la position des cinq à 2,5. Si aucun point de données égal ne s`est produit dans les étapes précédentes, entrez d dans la formule simple pour le coefficient de corrélation de rang de Spearman
et entrez le nombre de paires de données pour `n` pour trouver votre réponse.
Si des points de données similaires se sont produits au cours des étapes précédentes, utilisez la formule standard pour le coefficient de corrélation de rang de Spearman :
Près de -1 – Corrélation négative. Près de 0 – Pas de corrélation linéaire. Près de 1 – Corrélation positive. ré <- lire.csv("NAME_OF_YOU_CSV.csv") et appuyez sur Entrée cor(rang(d[,1]),rang(d[,2]))
Calculer le coefficient de corrélation de rang de spearman
Teneur
Avec le coefficient de corrélation de rang de Spearman, vous pouvez voir si deux variables sont liées par une fonction monotone (d.w.z. que si un nombre augmente, l`autre nombre augmente également ou vice versa). Pour calculer le coefficient de corrélation de rang de Spearman, vous devez ordonner et comparer les ensembles de données pour trouver d, puis entrer cette valeur dans la version standard ou simplifiée de la formule du coefficient de corrélation de rang de Spearman. Vous pouvez également calculer ce coefficient avec des formules Excel ou des commandes R.
Pas
Méthode 1 sur 3: Manuellement
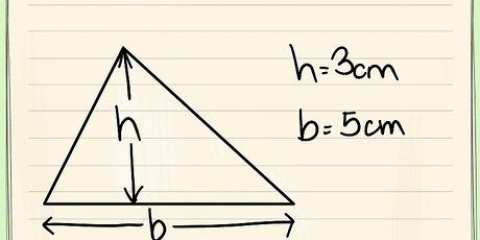
1. Dessinez votre table de données. Organise les informations dont vous avez besoin pour calculer le coefficient de corrélation de rang de Spearman. Vous avez besoin:
- 6 colonnes d`en-têtes, comme indiqué ci-dessus.
- Autant de lignes que vous avez de paires de données.
2. Remplissez les deux premières colonnes avec vos paires de données.
3. Disposez les points de données de la première colonne dans la troisième colonne, de 1 à m (le nombre total de points de données dont vous disposez). Donnez le numéro le plus bas à la position 1, le numéro suivant à la position 2, et ainsi de suite.
4. Faites de même avec la quatrième colonne qu`à l`étape 3, mais arrangez maintenant la deuxième colonne.
Dans l`exemple de droite, il y a deux cinq qui seraient normalement en position 2 et 3. C`est deux les mêmes chansons, donc prendre la moyenne de leurs positions. La moyenne de 2 et 3 est de 2,5, donc donnez la position des cinq à 2,5.
5. Dans la colonne « d », calculez la différence entre les deux positions dans chaque paire de données. En d`autres termes, si l`un a la position 1 et l`autre la position 3, la différence est de 2. (Positive ou négative n`a pas d`importance, puisque nous allons mettre cette différence au carré à l`étape suivante.)
6. Carrez les valeurs dans la colonne d et écrivez ces valeurs dans la colonne d.
sept. Ajouter tous les points de données dans la colonne d ensemble. Cette valeur est d.
8. Choisissez l`une des formules ci-dessous :
et entrez le nombre de paires de données pour `n` pour trouver votre réponse.
9. Interpréter le résultat. Cela peut varier entre -1 et 1.
Méthode 2 sur 3: Dans Excel
1. Créer de nouvelles colonnes avec les positions des colonnes existantes. Par exemple, si vous avez vos données dans la colonne A2:A11, vous utiliseriez la formule `=RANK(A2,A$2:A$11)` et étendriez la plage à toutes vos lignes et colonnes.
2. Traiter des points de données égaux comme décrit dans les étapes 3 et 4 de la méthode 1.
3. Dans une nouvelle cellule, effectuez un calcul de corrélation entre les deux colonnes avec une formule telle que `=CORREL(C2:C11,D2:D11)`. Dans ce cas, C et D sont les colonnes de position. Le coefficient de corrélation de rang de Spearman apparaît dans la cellule de corrélation.
Méthode 3 sur 3: Avec R
1. Installez R si vous ne l`avez pas déjà. (Voir https://www.r-projet.org/.)
2. Enregistrez vos données dans un fichier CSV, avec les données que vous souhaitez corréler dans les deux premières colonnes. Vous pouvez le faire avec le menu `Enregistrer sous`.
3. Ouvrez l`éditeur R. Si vous travaillez dans le terminal, exécutez simplement R. Lorsque vous êtes sur votre bureau, cliquez sur le logo R.
4. Tapez les commandes suivantes :
Des astuces
- La plupart des ensembles de données nécessitent au moins cinq paires de données pour établir une tendance (seulement trois paires ont été utilisées dans l`exemple pour faciliter l`exemple).
Mises en garde
- Le coefficient de corrélation de rang de Spearman ne montre la force de corrélation que si les points de données augmentent ou diminuent continuellement. Si le nuage de points des points de données montre une tendance différente, le coefficient de corrélation de rang de Spearman augmentera la corrélation ne pas afficher correctement.
- Cette formule est basée sur l`hypothèse qu`il n`y a pas de points de données égaux. S`il y a des points de données égaux, comme dans l`exemple ci-dessus, utilisez la définition suivante : le coefficient de corrélation produit-moment pour les rangs.
Articles sur le sujet "Calculer le coefficient de corrélation de rang de spearman"
Оцените, пожалуйста статью
Populaire