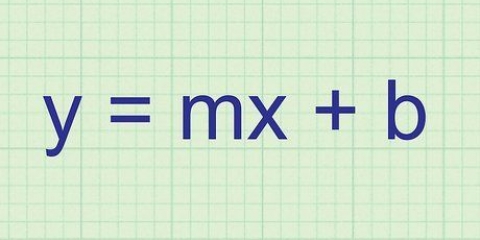Détermination du coefficient de corrélation

Teneur

Pas
Des astuces
Mises en garde

Le coefficient de corrélation, noté r ou , est la mesure de la corrélation linéaire (la relation, à la fois en force et en direction) entre deux variables. Il va de -1 à +1, en utilisant des signes plus et moins pour représenter la corrélation positive et négative. Si le coefficient de corrélation est exactement -1, alors la relation entre les deux variables est complètement négative ; si le coefficient de corrélation est exactement +1, alors la relation est complètement positive. Deux variables peuvent avoir une corrélation positive, une corrélation négative ou aucune corrélation du tout. Vous pouvez calculer la corrélation à la main, en utilisant des calculatrices de corrélation gratuites disponibles en ligne, ou en utilisant les fonctions statistiques d`une bonne calculatrice graphique.

Pas

Méthode 1 sur 4: Calculer le coefficient de corrélation à la main

Image intitulée Trouver le coefficient de corrélation Étape 1

1. Collectez d`abord vos données. Pour commencer à calculer une corrélation efficace, examinez d`abord les paires de données. Il est utile de les mettre dans un tableau, à la fois verticalement et horizontalement. Étiquetez chaque ligne ou colonne x et y.

Par exemple : supposons que vous ayez quatre paires de données pour X et oui. Le tableau pourrait alors ressembler à ceci :

x || oui
1 || 1
2 || 3
4 || 5
5 || sept

Image intitulée Trouver le coefficient de corrélation Étape 2

2. Calculer la moyenne de X. Pour calculer la moyenne, vous devez additionner toutes les valeurs de X additionner puis diviser par le nombre de valeurs.

En partant de l`exemple ci-dessus, notez que vous avez quatre valeurs pour X. Pour calculer la moyenne, comptez toutes les valeurs pour X et diviser par 4. Le calcul ressemble alors à ceci :

?? X = (1 + 2 + 4 + 5) / 4

${displaystyle mu _{x}=(1+2+4+5)/4}$

?? X = 12 / 4

${displaystyle mu _{x}=12/4}$

?? X = 3

${displaystyle mu _{x}=3}$

Image intitulée Trouver le coefficient de corrélation Étape 3

3. Trouver la moyenne de oui. Pour obtenir la moyenne de oui Pour le trouver, suivez les mêmes étapes, en additionnant toutes les valeurs de y puis en divisant par le nombre de valeurs.

Dans l`exemple ci-dessus, vous avez également quatre valeurs pour oui. Additionnez toutes ces valeurs puis divisez par 4. Les calculs ressembleront alors à ceci :

?? oui = (1 + 3 + 5 + sept) / 4

${displaystyle mu _{y}=(1+3+5+7)/4}$

?? oui = 16 / 4

${displaystyle mu _{y}=16/4}$

?? oui = 4

${displaystyle mu _{y}=4}$

Image intitulée Trouver le coefficient de corrélation Étape 4

4. Déterminer l`écart type de X. Une fois que vous avez vos moyens, vous pouvez calculer l`écart type. Utilisez la formule pour cela :

?? X = \sqrt{} 1 m - 1 ?? (X - {??}_{X})^{2}

${displaystyle sigma _{x}={sqrt {{frac {1}{n-1}}Sigma (x-mu _{x})^{2}}}}$

Avec les exemples de données, vos calculs ressembleront à ceci :

?? X = \sqrt{} 1 4 - 1 * ((1 - 3)^{2} + (2 - 3)^{2} + (4 - 3)^{2} + (5 - 3)^{2})

${displaystyle sigma _{x}={sqrt {{frac {1}{4-1}}*((1-3)^{2}+(2-3)^{2}+(4 -3)^{2}+(5-3)^{2})}}}$

?? X = \sqrt{} \frac{1}{3} * (4 + 1 + 1 + 4)

${displaystyle sigma _{x}={sqrt {{frac {1}{3}}*(4+1+1+4)}}}$

?? X = \sqrt{} \frac{1}{3} * (dix)

${displaystyle sigma _{x}={sqrt {{frac {1}{3}}*(10)}}}$

?? X = \sqrt{\frac{dix}{3}}

${displaystyle sigma _{x}={sqrt {frac {10}{3}}}}$

?? X = 1, 83

${displaystyle sigma _{x}=1.83}$

Image intitulée Trouver le coefficient de corrélation Étape 5

5. Calculer l`écart type de oui. En utilisant les mêmes étapes de base, trouvez l`écart type de oui. Vous allez utiliser la même formule, en utilisant les points de données pour y.

Avec les exemples de données, vos calculs ressembleront à ceci :

?? oui = \sqrt{} 1 4 - 1 * ((1 - 4)^{2} + (3 - 4)^{2} + (5 - 4)^{2} + (sept - 4)^{2})

${displaystyle sigma _{y}={sqrt {{frac {1}{4-1}}*((1-4)^{2}+(3-4)^{2}+(5 -4)^{2}+(7-4)^{2})}}}$

?? oui = \sqrt{} \frac{1}{3} * (9 + 1 + 1 + 9)

${displaystyle sigma _{y}={sqrt {{frac {1}{3}}*(9+1+1+9)}}}$

?? oui = \sqrt{} \frac{1}{3} * (20)

${displaystyle sigma _{y}={sqrt {{frac {1}{3}}*(20)}}}$

?? oui = \sqrt{\frac{20}{3}}

${displaystyle sigma _{y}={sqrt {frac {20}{3}}}}$

?? oui = 2, 58

${displaystyle sigma _{y}=2.58}$

Image intitulée Trouver le coefficient de corrélation Étape 6

6. Afficher la formule de base pour déterminer un coefficient de corrélation. La formule de calcul d`un coefficient de corrélation utilise des moyennes, des écarts types et le nombre de paires dans un ensemble de données (représenté par m). Le coefficient de corrélation lui-même est représenté par la lettre minuscule r ou la lettre grecque (rho). Pour cet article, nous utiliserons la formule connue sous le nom de coefficient de corrélation de Pearson, comme indiqué ci-dessous :

?? = (1 m - 1) ?? (X - ?? X {??}_{X}) * (oui - ?? oui {??}_{oui})

${displaystyle rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}} }right)*left({frac {y-mu _{y}}{sigma _{y}}}right)}$

Vous pouvez remarquer de légères variations dans la formule, ici ou dans d`autres explications. Par exemple, certains utiliseront la notation grecque avec rho et sigma, tandis que d`autres utiliseront r et s. Certaines explications peuvent utiliser des formules légèrement différentes, mais elles seront mathématiquement équivalentes à celle-ci.

Image intitulée Trouver le coefficient de corrélation Étape 7

sept. Déterminer le coefficient de corrélation. Vous disposez maintenant des moyennes et des écarts types de vos variables, vous pouvez donc passer à la formule du coefficient de corrélation. Souviens-toi que m représente le nombre de valeurs que vous avez. Vous avez déjà calculé les autres informations pertinentes dans les étapes ci-dessus.

En utilisant les exemples de données, vous pouvez saisir les données dans la formule du coefficient de corrélation et les calculer comme ceci :

?? = (1 m - 1) ?? (X - ?? X {??}_{X}) * (oui - ?? oui {??}_{oui})

${displaystyle rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}} }right)*left({frac {y-mu _{y}}{sigma _{y}}}right)}$

?? = (\frac{1}{3}) *

${displaystyle rho =left({frac {1}{3}}right)*}$ [

(1 - 3 1, 83) * (1 - 4 2, 58) + (2 - 3 1, 83) * (3 - 4 2, 58)

${displaystyle left({frac {1-3}{1.83}}right)*left({frac {1-4}{2.58}}right)+left({ frac {2- 3}{1.83}}right)*left({frac {3-4}{2.58}}right)}$

+ (4 - 3 1, 83) * (5 - 4 2, 58) + (5 - 3 1, 83) * (sept - 4 2, 58)

${displaystyle +left({frac {4-3}{1.83}}right)*left({frac {5-4}{2.58}}right)+left({ frac {5 -3}{1.83}}right)*left({frac {7-4}{2.58}}right)}$ ]

?? = (\frac{1}{3}) * (6 + 1 + 1 + 6 4, 721)

${displaystyle rho =left({frac {1}{3}}right)*left({frac {6+1+1+6}{4,721}}right)}$

?? = (\frac{1}{3}) * 2, 965

${displaystyle rho =left({frac {1}{3}}right)*2,965}$

?? = (2, 965 3)

${displaystyle rho =left({frac {2,965}{3}}right)}$

?? = 0, 988

${style d`affichage rho =0.988}$

Image intitulée Trouver le coefficient de corrélation Étape 8

8. Interpréter le résultat. Pour cet ensemble de données, le coefficient de corrélation est de 0,988. Ce nombre vous dit deux choses sur les données. Regardez le signe du nombre et la taille du nombre.

Puisque le coefficient de corrélation est positif, vous pouvez dire qu`il existe une corrélation positive entre les données x et les données y. Cela signifie qu`à mesure que les valeurs x augmentent, vous vous attendez à ce que les valeurs y augmentent également.

Étant donné que le coefficient de corrélation est très proche de +1, les données x et y sont très étroitement liées. Si vous deviez représenter graphiquement ces points, vous verriez qu`ils sont une très bonne approximation d`une ligne droite.

Méthode 2 sur 4: Utilisation de calculateurs de corrélation en ligne

Image intitulée Trouver le coefficient de corrélation Étape 9

1. Rechercher en ligne des calculateurs de corrélation. Mesurer la corrélation est un calcul assez standard pour les statisticiens. Le calcul peut devenir très fastidieux pour les grands ensembles de données s`il est fait à la main. Par conséquent, de nombreuses sources ont rendu des calculs de corrélation communs disponibles en ligne. Utilisez n`importe quel moteur de recherche et entrez le terme de recherche « calculateur de corrélation ».

Image intitulée Trouver le coefficient de corrélation Étape 10

2. Pour les données en. Veuillez lire attentivement les instructions sur le site Web afin de pouvoir saisir correctement les données. Il est important que les paires de données soient conservées dans l`ordre ou vous obtiendrez un résultat de corrélation incorrect. Différents sites Web utilisent un formatage différent pour saisir des données.

Par exemple : sur le site http://ncalculateurs.com/statistics/correlation-coefficient-calculator.htm trouver une case horizontale pour saisir les valeurs x et une deuxième case horizontale pour saisir les valeurs y. Vous entrez les termes séparés uniquement par des virgules. Ainsi, l`ensemble de données x calculé plus tôt dans cet article doit être entré sous la forme 1,2,4,5. L`ensemble de données y est entré comme 1,3,5,7.

Sur un autre site, http://www.de l`alcool.com/calculators/statistics/correlation-coefficient/, vous pouvez saisir des données à la fois horizontalement et verticalement, tant que vous gardez les points de données dans l`ordre.

Image intitulée Trouver le coefficient de corrélation Étape 11

3. Calculer les résultats. Ces sites de calcul sont populaires car, en général, après avoir entré les données, il suffit de cliquer sur le bouton `Calculer` -- le résultat apparaîtra automatiquement.

Méthode 3 sur 4: Utiliser une calculatrice graphique

Image intitulée Trouver le coefficient de corrélation Étape 12

1. Entrez vos coordonnées. Sur votre calculatrice graphique, activez la fonction statistiques puis sélectionnez la commande `Modifier`.

Chaque calculatrice a des commandes de touches légèrement différentes. Cet article fournit des instructions spécifiques pour la Texas Instruments TI-86.
Entrez dans la fonction Stat en appuyant sur [2nd]-Stat (au-dessus de la touche `+`) puis sur F2-Edit.

Image intitulée Trouver le coefficient de corrélation Étape 13

2. Effacer toutes les anciennes données enregistrées. La plupart des calculatrices conserveront les données statistiques jusqu`à ce qu`elles soient effacées. Pour vous assurer de ne pas confondre les anciennes données avec les nouvelles données, vous devez d`abord effacer toutes les informations précédemment stockées.

Utilisez les touches fléchées pour déplacer le curseur pour mettre en surbrillance la catégorie `xStat`. Appuyez ensuite sur « Effacer » et « Entrer. Cela devrait effacer toutes les valeurs de la colonne xStat.

Utilisez les touches fléchées pour mettre en surbrillance la catégorie `yStat`. Appuyez sur « Effacer » et « Entrée » pour effacer également les données de cette colonne.

Image intitulée Trouver le coefficient de corrélation Étape 14

3. Entrez vos valeurs de données. Utilisez les touches fléchées pour déplacer le curseur sur le premier espace sous l`en-tête xStat. Tapez votre première valeur de données, puis appuyez sur Entrée. Vous devriez voir l`espace en bas de l`écran `xStat(1)=__` où votre valeur remplit l`espace vide. Lorsque vous appuyez sur Entrée, les données rempliront le tableau, le curseur passera à la ligne suivante et la ligne en bas de l`écran devrait maintenant indiquer `xStat(2)=__`.

Continuer à saisir toutes les valeurs x.

Une fois que vous avez entré les valeurs x, utilisez les touches fléchées pour passer à la colonne yStat et entrez les valeurs y.

Lorsque toutes les données ont été saisies, appuyez sur Quitter pour effacer l`écran et quitter le menu Stat.

Image intitulée Trouver le coefficient de corrélation Étape 15

4. Calculer les statistiques de régression linéaire. Le coefficient de corrélation est une mesure de la mesure dans laquelle les données se rapprochent d`une ligne droite. Une calculatrice graphique avec des fonctions statistiques peut calculer très rapidement la ligne de meilleur ajustement et le coefficient de corrélation.

Entrez dans la fonction Stat puis appuyez sur le bouton Calc. Sur la TI-86 c`est [2nd][Stat][F1].

Choisissez les calculs de régression linéaire. Sur la TI-86, c`est [F3], étiqueté "LinR.` L`écran graphique affichera alors la ligne `LinR _` avec un curseur clignotant.

Vous devez maintenant saisir les noms des deux variables que vous souhaitez calculer. Ce sont xStat et yStat.

Sur la TI-86, sélectionnez la liste des noms (`Names`) en appuyant sur [2nd][List][F3].

La ligne du bas de votre écran devrait maintenant afficher les variables disponibles. Choisissez [xStat] (c`est probablement le bouton F1 ou F2), puis entrez une virgule puis [yStat].

Appuyez sur Entrée pour calculer les données

Image intitulée Trouver le coefficient de corrélation Étape 16

5. Interpréter les résultats. Lorsque vous appuyez sur Entrée, la calculatrice calcule immédiatement les informations suivantes pour les données que vous avez saisies :

oui = une + b X

${style d`affichage y=a+bx}$ : C`est la formule générale pour une ligne droite. Cependant, au lieu du bien connu `y=mx+b`, celui-ci est présenté dans l`ordre inverse.

une =

${style d`affichage a=}$ . C`est la valeur de l`intersection avec l`axe des y de la ligne qui correspond le mieux.

b =

${style d`affichage b=}$ . C`est la pente de la droite qui correspond le mieux.

correct =

${displaystyle {text{corr}}=}$ . C`est le coefficient de corrélation.

m =

${style d`affichage n=}$ . C`est le nombre de paires de données utilisées dans le calcul.

Méthode 4 sur 4: Répéter les bases

Image intitulée Trouver le coefficient de corrélation Étape 17

1. Comprendre le concept de corrélation. La corrélation fait référence à la relation statistique entre deux quantités. Le coefficient de corrélation est un nombre unique que vous pouvez calculer pour deux ensembles de points de données. Le nombre est toujours quelque chose entre -1 et +1, et indique à quel point les deux ensembles de données sont étroitement liés.

Par exemple, si vous mesuriez la taille et l`âge d`enfants jusqu`à environ 12 ans, vous vous attendriez à trouver une forte corrélation positive. En vieillissant, les enfants ont tendance à grandir.
Un exemple de corrélation négative consiste à comparer le temps qu`une personne passe à pratiquer le golf et le score de golf de cette personne. Au fur et à mesure que la pratique progresse, le score devrait baisser.
En fin de compte, vous vous attendriez à peu de corrélation, positive ou négative, entre la pointure d`une personne, par exemple, et ses notes aux examens.

Image intitulée Trouver le coefficient de corrélation Étape 18

2. Calculer la moyenne. La moyenne arithmétique, ou "moyenne", d`un ensemble de données est calculée en additionnant toutes les valeurs des données, puis en divisant par le nombre de valeurs dans l`ensemble. Lorsque vous souhaitez déterminer le coefficient de corrélation de vos données, vous devez calculer la moyenne de chaque ensemble de données.

La moyenne d`une variable est indiquée par la variable avec une ligne horizontale au-dessus. Ceci est souvent appelé `x-bar` ou `y-bar` pour les ensembles de données de x et y. Alternativement, la moyenne peut être désignée par la lettre grecque minuscule (mu). Par exemple, pour représenter la moyenne des points de données de x, vous pouvez utiliser μ_X ou (x).

Par exemple, si vous avez un ensemble de x (1,2,5,6,9,10), la moyenne de ces données serait calculée comme suit :

?? X = (1 + 2 + 5 + 6 + 9 + dix) / 6

${displaystyle mu _{x}=(1+2+5+6+9+10)/6}$

?? X = 33 / 6

${displaystyle mu _{x}=33/6}$

?? X = 5, 5

${displaystyle mu _{x}=5.5}$

Image intitulée Trouver le coefficient de corrélation Étape 19

3. Connaître l`importance de l`écart type. Dans les statistiques, l`écart type mesure la variation, montrant l`écart des nombres par rapport à la moyenne. Un groupe de nombres avec un faible écart type sont assez proches les uns des autres. Un groupe de nombres avec un écart type élevé est plus dispersé.

Comme symbole, l`écart type est exprimé avec la lettre minuscule s ou la lettre grecque (sigma). Ainsi, l`écart type des données x s`écrit sous la forme s_X ou_X.

Image intitulée Trouver le coefficient de corrélation Étape 20

4. Reconnaître la notation de sommation. L`opérateur de sommation est l`un des opérateurs les plus courants en mathématiques, représentant une somme de valeurs. Il est représenté par la lettre majuscule grecque, sigma ou ∑.

Par exemple, si vous avez un ensemble de points de données x (1,2,5,6,9,10), alors ∑x signifie :

1+2+5+6+9+10 = 33

Des astuces

Le coefficient de corrélation est parfois appelé « coefficient de corrélation produit-moment de Pearson », en l`honneur de Karl Pearson, son développeur.
En général, un coefficient de corrélation supérieur à 0,8 (positif ou négatif) représente une forte corrélation ; un coefficient de corrélation inférieur à 0,5 (à nouveau positif ou négatif) représente un faible coefficient de corrélation.

Mises en garde

La corrélation montre que deux ensembles de données sont en quelque sorte connectés. Attention toutefois à ne pas interpréter cela comme une relation causale. Par exemple, si vous comparez les tailles de chaussures des gens et leur taille, vous trouverez probablement une forte corrélation positive. Les personnes plus grandes ont généralement des pieds plus grands. Cependant, cela ne signifie pas que devenir grand fera grandir vos pieds, ou que de grands pieds vous feront grandir. Ils arrivent juste ensemble.