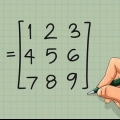Déterminer le déterminant d'une matrice 3x3 : 12 étapes (avec photos)

Teneur

Pas
- Partie 1 sur 2: Détermination du déterminant
- Partie 2 sur 2: Simplifier le problème
Des astuces

Le déterminant d`une matrice est largement utilisé en mathématiques, en algèbre linéaire et en géométrie supérieure. En dehors du monde scientifique, les informaticiens et programmeurs utilisent fréquemment les déterminants des matrices. Lisez cet article pour déterminer le déterminant d`une matrice 3x3.

Pas

Partie 1 sur 2: Détermination du déterminant

Image intitulée Trouver le déterminant d`une matrice 3X3 Étape 1

1. Écrivez votre matrice 3 x 3. Nous partons d`une matrice 3 x 3 A et essayons le déterminant |A| aimer ça. Nous utilisons la notation générale suivante pour la matrice (et c`est notre exemple de matrice) :

$m = (\begin{matrix} une \end{matrix} 11 {une}_{12} {une}_{13} {une}_{21} & {une}_{22} & {une}_{23} {une}_{31} & {une}_{32} & {une}_{33}) = (\begin{matrix} 1 & 5 & 3 \\ 2 & 4 & sept \\ 4 & 6 & 2 \end{matrix})$ $M={begin{pmatrix}a_{{11}}&a_{{12}}&a_{{13}}\a_{{21}}&a_{{22}}&a_{ {23}}\a_{{31}}&a_{{32}}&a_{{33}}end{pmatrix}}={begin{pmatrix}1&5&3\2& 4&7\4&6&2end{pmatrix}}$

Image intitulée Trouver le déterminant d`une matrice 3X3 Étape 2

2. Choisissez une ligne ou une colonne. Ce sera votre ligne ou colonne de référence. Vous obtiendrez la même réponse quel que soit celui que vous choisissez. Maintenant, choisissez simplement la première ligne. Plus tard, nous vous conseillerons sur la façon de choisir l`option la plus facile à calculer.

Choisissons la première ligne de notre exemple de matrice A. Entoure le 1 5 3. En termes généraux, encerclez un₁₁ une₁₂ une₁₃.

Image intitulée Trouver le déterminant d`une matrice 3X3 Étape 3

3. Barrer la ligne et la colonne du premier élément. Regardez la ligne ou la colonne que vous avez encerclée et sélectionnez le premier élément. Tracez une ligne à travers la ligne et la colonne correspondantes. Si tout se passe bien, cela donne maintenant quatre nombres. Nous traitons cela comme une matrice 2 x 2.

Dans notre exemple, la ligne de référence est 1 5 3. Ce premier élément est dans la ligne 1 et la colonne 1. Rayez complètement la ligne 1 et la colonne 1. Notez les éléments restants sous forme deMatrice 2 x 2:

~~1 5 3~~
2 4 7
4 6 2

Image intitulée Trouver le déterminant d`une matrice 3X3 Étape 4

4. Déterminer le déterminant de la matrice 2 x 2. N`oubliez pas : la matrice

(\begin{matrix} une & b \\ c & ré \end{matrix})

${begin{pmatrix}a&b\c&dend{pmatrix}}$ a un déterminant de annonce - avant JC. Vous le savez en traçant une croix (X) à travers la matrice 2 x 2. Multiplier les deux nombres reliés par le du X. Soustraire ensuite le produit des deux nombres reliés par le /. Utilisez cette formule pour calculer le déterminant de la matrice que vous venez de trouver.

Dans notre exemple, le déterminant de la matrice est

(\begin{matrix} 4 & sept \\ 6 & 2 \end{matrix})

${begin{pmatrix}4&7\6&2end{pmatrix}}$ = 4 * 2 - 7 * 6 = -34.

Ce déterminant est appelé le mineur de l`élément que nous avons choisi dans notre matrice d`origine. Dans ce cas, nous avons le mineur de une₁₁ l`a trouvé.

Image intitulée Trouver le déterminant d`une matrice 3X3 Étape 5

5. Multipliez la réponse par l`élément que vous avez choisi. N`oubliez pas que vous avez sélectionné un élément de votre ligne (ou colonne) de référence lorsque vous avez décidé quelle ligne et colonne rayer. Multipliez cet élément par le déterminant que vous venez de calculer pour la matrice 2x2.

Dans notre exemple, nous avons un₁₁ sélectionné, qui a une valeur de 1. Multipliez cela par -34 (le déterminant de la matrice 2x2) pour obtenir 1*-34 = -34 pour obtenir.

Image intitulée Trouver le déterminant d`une matrice 3X3 Étape 6

6. Déterminez le signe de votre réponse. Multipliez maintenant la réponse par 1 ou par -1 pour obtenir le cofacteur de votre élément choisi. Celui que vous utilisez dépend de la position de l`élément dans la matrice 3x3. Mémorisez le tableau simple suivant pour savoir quel élément cause quoi :

+ - +
- + -
+ - +

Parce que nous une₁₁ avoir choisi, marqué d`un +, on multiplie le nombre par +1 (autrement dit, on n`en fait rien). La réponse est encore -34.

Une autre façon de déterminer le signe est avec la formule (-1), où je et j former la ligne et la colonne de l`élément.

Image intitulée Trouver le déterminant d`une matrice 3X3 Étape 7

sept. Répétez ce processus pour le deuxième élément de votre ligne ou colonne de référence. Continuez avec la matrice 3x3 d`origine, avec la ligne ou la colonne que vous avez encerclée plus tôt. Répétez le même processus avec cet élément :

Traversez la ligne et la colonne de cet élément. Dans ce cas, vous sélectionnez l`élément a₁₂ (avec la valeur 5). Traversez la première ligne (1 5 3) et la deuxième colonne

(\begin{matrix} 5 \\ 4 \\ 6 \end{matrix})

${begin{pmatrix}5\4\6end{pmatrix}}$ .

Traiter les éléments restants comme une matrice 2x2. Dans notre exemple, la matrice est

(\begin{matrix} 2 & sept \\ 4 & 2 \end{matrix})

${begin{pmatrix}2&7\4&2end{pmatrix}}$

Déterminer le déterminant de cette matrice 2x2. Utilisez la formule ad - bc. (2*2 - 7*4 = -24)

Multipliez cela par l`élément choisi de la matrice 3x3. -24 * 5 = -120

Déterminer s`il faut multiplier par -1. Utilisez la table de caractères ou la formule (-1). Nous avons l`élément a₁₂ choisi, et c`est un - sur la table des caractères. Nous devons changer le signe de notre réponse : (-1)*(-120) = 120.

Image intitulée Trouver le déterminant d`une matrice 3X3 Étape 8

8. Répétez pour le troisième élément. Vous devez maintenant trouver un cofacteur. Calculez i pour le troisième terme de votre ligne ou colonne de référence. Voici une explication rapide sur la façon de calculer le cofacteur de ₁₃ dans notre exemple :

Croisez la ligne 1 et la colonne 3 et obtenez

(\begin{matrix} 2 & 4 \\ 4 & 6 \end{matrix})

${begin{pmatrix}2&4\4&6end{pmatrix}}$

Son déterminant est 2*6 - 4*4 = -4.

Multipliez cela par l`élément a₁₃: -4 * 3 = -12.

élément a₁₃ est un + sur la table des caractères, donc la réponse est -12.

Image intitulée Trouver le déterminant d`une matrice 3X3 Étape 9

9. Additionner les trois résultats ensemble. C`est la dernière étape. Vous avez calculé des cofacteurs, un pour chaque élément dans une seule ligne ou colonne. Additionnez-les et vous avez trouvé le déterminant de la matrice 3x3.

Dans notre exemple, le déterminant est -34 + 120 + -12 = 74.

Partie 2 sur 2: Simplifier le problème

Image intitulée Trouver le déterminant d`une matrice 3X3 Étape 10

1. Choisissez la référence avec le plus de zéros. N`oubliez pas que vous chaque peut choisir une ligne ou une colonne comme référence. Vous obtiendrez la même réponse, peu importe ce que vous choisissez. Si vous choisissez une ligne ou une colonne avec des zéros, il vous suffit de calculer le cofacteur des éléments qui ne sont pas nuls. La raison en est la suivante:

Supposons que vous choisissiez la ligne 2, avec les éléments a₂₁, une₂₂, et un₂₃. Pour résoudre ce problème, nous examinons trois matrices 2x2 différentes. Supposons que nous appelions cela A₂₁, une₂₂ et un₂₃.
Le déterminant de la matrice 3x3 est un₂₁|A₂₁| - une₂₂|A₂₂| + un₂₃|A₂₃|.
Si les termes un₂₂ et un₂₃ sont tous les deux à 0, alors notre formule devient₂₁|A₂₁| - 0*|A₂₂| + 0*|A₂₃| = un₂₁|A₂₁| - 0 + 0 = un₂₁|A₂₁|. Il ne nous reste plus qu`à calculer le cofacteur d`un seul élément.

Image intitulée Trouver le déterminant d`une matrice 3X3 Étape 11

2. Additionnez les lignes pour simplifier la matrice. Si vous prenez les valeurs d`une ligne et les ajoutez à une autre ligne, le déterminant de la matrice ne changera pas. Idem pour les colonnes. Vous pouvez le faire à plusieurs reprises - ou multiplier les valeurs par une constante avant d`ajouter - pour obtenir autant de zéros que possible dans la matrice. Cela peut vous faire économiser beaucoup de travail.

Par exemple, supposons que vous ayez une matrice 3x3 :

(\begin{matrix} 9 & - 1 & 2 \\ 3 & 1 & 0 \\ sept & 5 & - 2 \end{matrix})

${begin{pmatrix}9&-1&2\3&1&0\7&5&-2end{pmatrix}}$

Tous les 9 en position a₁₁ pour s`en débarrasser, on peut multiplier la deuxième ligne par -3 et ajouter le résultat à la première. La nouvelle première ligne devient alors [9 -1 2] + [-9 -3 0] = [0 -4 2].

La nouvelle matrice est

(\begin{matrix} 0 & - 4 & 2 \\ 3 & 1 & 0 \\ sept & 5 & - 2 \end{matrix})

${begin{pmatrix}0&-4&2\3&1&0\7&5&-2end{pmatrix}}$ Essayez d`utiliser la même astuce pour les colonnes, pour₁₂ faire un 0.

Image intitulée Trouver le déterminant d`une matrice 3X3 Étape 12

3. Apprenez l`astuce pour résoudre les matrices triangulaires. Dans ces cas particuliers, le déterminant est simplement le produit des éléments le long de la diagonale principale, à partir d`un₁₁ en haut à gauche à un₃₃ en bas à droite. Nous parlons toujours de matrices 3x3, mais les matrices «triangulaires» ont des modèles de valeurs spéciaux qui pas nul sont:

Matrice du triangle supérieur : tous les éléments non nuls sont sur ou au-dessus de la diagonale principale. Toutes les valeurs ci-dessous sont nulles.

Matrice du triangle inférieur : tous les éléments non nuls sont sur ou en dessous de la diagonale principale.

Matrice diagonale : tous les éléments non nuls sont sur la diagonale principale. (Un sous-ensemble de ce qui précède.)

Des astuces

Cette méthode peut être utilisée pour des matrices carrées de n`importe quelle taille. Par exemple, si vous l`utilisez pour une matrice 4x4, vous gardez après le "barrer" une matrice 3x3, pour laquelle vous pouvez calculer le déterminant comme indiqué ci-dessus. Soyez prévenu, car le faire à la main sera très ennuyeux!
Si tous les éléments d`une ligne ou d`une colonne sont égaux à 0, alors le déterminant de cette matrice est égal à 0.