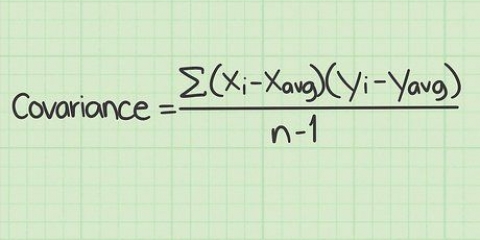Transposer une matrice : 11 étapes (avec des images)

Teneur

Pas
Des astuces

Une transposition matricielle est un outil mathématique utile pour comprendre la structure des matrices. Les fonctions que vous connaissez peut-être déjà des matrices, telles que le carré et la symétrie, influencent les résultats de la transposition de manière évidente. La transposition sert également à exprimer des vecteurs sous forme de matrices, ou à calculer les produits de vecteurs. Lorsqu`il s`agit de matrices complexes, le concept étroitement lié de transposition conjuguée vous aidera à résoudre de nombreux problèmes.

Pas

Partie1 sur 3: Transposer une matrice

Image intitulée Transposer une matrice Étape 1

1. Commencez avec n`importe quelle matrice. Vous pouvez transposer n`importe quelle matrice quel que soit le nombre de lignes et de colonnes. Les matrices carrées, avec un nombre égal de lignes et de colonnes, sont les plus transposées, nous utiliserons donc une simple matrice carrée comme exemple :

matrice une =
1 2 3
4 5 6
7 8 9

Image intitulée Transposer une matrice Étape 2

2. Faire de la première ligne de la matrice la première colonne de la transposition. Réécrivez la première ligne de la matrice en colonne :

Transposition de la matrice A = A

Première colonne de A :
1
2
3

Image intitulée Transposer une matrice Étape 3

3. Répétez pour les rangées restantes. La deuxième ligne de la matrice d`origine devient la deuxième colonne de la transposition. Répétez ce schéma jusqu`à ce que vous ayez transformé chaque ligne en colonne :

une =
1 4 7
2 5 8
3 6 9

Image intitulée Transposer une matrice Étape 4

4. Pratique sur une matrice non carrée. La transposition est exactement la même pour une matrice non carrée. Vous réécrivez la première ligne en tant que première colonne, la deuxième ligne en tant que deuxième colonne, et ainsi de suite. Voici un exemple codé par couleur pour vous montrer où se trouvent les éléments :

matrice z =
4 7 2 1
3 9 8 6

matrice z =
4 3
sept 9
2 8
1 6

Image intitulée Transposer une matrice Étape 5

5. Exprimer mathématiquement la transposition. Le concept est assez simple, mais c`est bien de pouvoir le décrire en termes mathématiques. Aucun jargon n`est nécessaire en dehors de la notation matricielle de base :

Si la matrice B est un m X m (m lignes et n colonnes), alors la matrice transposée B est une m X m matrice (n lignes et m colonnes).

Pour chaque élément b_xy (X-la, oui-la colonne) dans B, la matrice B a un élément égal sur b_yx (oui-la ligne, X-la colonne).

Partie 2 sur 3: Cas particuliers

Image intitulée Transposer une matrice Étape 6

1. (M = M. La transposition d`une transposition est la matrice d`origine. Cela a beaucoup de sens, puisque vous ne faites qu`échanger les lignes et les colonnes. Les échanger à nouveau vous ramènera au début.

Image intitulée Transposer une matrice Étape 7

2. Incliner les matrices carrées sur la diagonale principale. Dans une matrice carrée, une transposition "inclinera" la matrice le long de la diagonale principale. En d`autres termes, les éléments d`une ligne diagonale de l`élément a₁₁ dans le coin inférieur droit reste le même. Les autres éléments se déplaceront sur la diagonale et se retrouveront à la même distance de la diagonale, du côté opposé.

Si vous ne pouvez pas visualiser cela, dessinez une matrice 4x4 sur un morceau de papier. Maintenant, repliez la diagonale principale. Voyez-vous comment les éléments un₁₄ et un₄₁ touche chacun des autres? Ils échangent leurs places dans la transposition, comme n`importe quelle autre paire qui se touche une fois pliée.

Image intitulée Transposer une matrice Étape 8

3. Transposer une matrice symétrique. Une matrice symétrique est symétrique par rapport à la diagonale principale. Si nous utilisons le `tilt` ou le `fold` comme décrit ci-dessus, nous pouvons immédiatement voir que rien ne change. Toutes les paires d`éléments qui échangent des places étaient déjà identiques. En fait, c`est la façon standard de définir une matrice symétrique. Si matrice A = A, alors la matrice A est symétrique.

Partie3 sur 3: Transposition conjuguée d`une matrice complexe

Image intitulée Transposer une matrice Étape 9

1. Commencer avec une matrice complexe. Les matrices complexes ont des éléments avec une composante réelle et imaginaire. Bien que vous puissiez effectuer une transposition régulière de ces matrices, la plupart des calculs pratiques sont plutôt des transpositions conjuguées.

Matrice C =
2+je 3-2je
0+je 5+0je

Image intitulée Transposer une matrice Étape 10

2. Prendre la conjugaison complexe. La conjugaison complexe change le signe des composantes imaginaires, sans changer les composantes réelles. Effectuer cette opération pour tous les éléments de la matrice.

Conjugaison complexe de C =
2-je 3+2je
0-je 5-0je

Image intitulée Transposer une matrice Étape 11

3. Transposer les résultats. Prendre une conversion ordinaire du résultat. La matrice avec laquelle vous vous retrouvez est la transposition conjuguée de la matrice d`origine.

Transposition conjuguée de C = C =
2-je 0-je
3+2je 5-0je

Des astuces

Cet article utilise la notation A pour désigner la conversion de la matrice A. La notation A` ou Ã signifie la même chose.
Cet article fait référence à la conversion conjuguée de la matrice A en A, la notation la plus courante en algèbre linéaire. Les physiciens quantiques utilisent souvent A à la place. A* est une autre option, mais essayez d`éviter cela car certaines sources utiliseront ce symbole pour indiquer une conjugaison complexe.